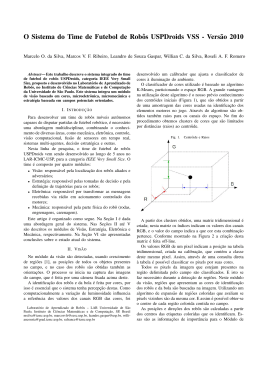
CONTROLE SERVO VISUAL PARA O RASTREAMENTO DE TRAJETÓRIA
DEFINIDA POR RETAS: TEORIA E RESULTADOS EXPERIMENTAIS
Pedro M. Shiroma∗
José R.H. Carvalho∗
[email protected]
[email protected]
Geraldo F. Silveira
∗
[email protected]
∗
Centro de Pesquisas Renato Archer - CenPRA
Divisão de Robótica e Visão Computacional - DRVC
Rodovia Dom Pedro I, km 143,6 CEP 13082-120, Campinas-SP, Brasil
ABSTRACT
1 INTRODUÇÃO
This work proposes a visual servoing solution to the hallway following problem applied to a mobile robot. The goal is to follow
a line parallel to the corridor that can be defined as the intersection of the floor with the wall. The problem consists in capturing
the image, to segment and extract the line, real-time tracking and
parameters computing of the line and control signals determination based on the so called interaction matrix and robot Jacobian.
The results were obtained using a Nomad 200 mobile robot with
a non-calibrated CCD camera mounted on a pan-tilt as the experimental setup.
O uso da visão como fonte de informações sensoriais é amplamente pesquisado em robótica. Tal interesse deve-se principalmente ao fato deste sensor (câmera) ser um elemento de medida
passivo, ou seja, que não necessita de contato fı́sico, apresentar
alta densidade de dados por imagem, amplo campo de cobertura e boa taxa de amostragem a um baixo custo. O aumento do
desempenho dos recursos computacionais aliado a novos resultados em áreas como visão computacional, processamento de imagens e controle de sistemas permitiu incluir a informação visual
dentro de uma malha de controle fechada, criando um campo
atualmente conhecido como controle servo visual.
KEYWORDS: Vision-based control, mobile robotic, robot navigation, visual servoing.
RESUMO
Este trabalho propõe uma solução utilizando técnicas de controle servo visual (visual servoing) para o problema de seguimento
de trajetória aplicado a um robô móvel. O objetivo é percorrer
uma reta definida pelo rodapé de um dos corredores do laboratório. O problema envolve as tarefas de captura da imagem,
segmentação e extração do rodapé, rastreamento e cálculo dos
parâmetros da reta em tempo real, determinação da velocidade
da câmera necessária para realizar a tarefa, baseado na chamada matriz de interação, e posterior transformação para o sistema
de coordenadas dos atuadores. Os resultados foram obtidos utilizando como plataforma experimental um robô móvel Nomad
200, com uma câmera CCD não-calibrada montada sobre um
pan-tilt.
PALAVRAS-CHAVE: Controle baseado em visão, controle servo
visual, robôs móveis, navegação robótica.
Neste trabalho, a metodologia proposta por Espiau et al. (1992)
é aplicado ao controle servo visual de uma classe de robô móvel
não-holonômico com rodas. O problema consiste em percorrer
os corredores do laboratório utilizando apenas a informação visual para guiar-se sem, entretanto, determinar a postura do alvo
em relação ao robô, o que envolveria a reconstrução 3D da cena e a calibração da câmera. A solução baseia-se na chamada
matriz de interação cujo propósito é estender o Jacobiano do
robô ao plano imagem através de primitivas geométricas. Tal
abordagem difere das soluções clássicas onde o controle é realizado no espaço Cartesiano, necessitando apenas de uma única
reta na imagem e fornece uma formulação matemática que permite o desenvolvimento de diversas outras tarefas servo visuais.
Resultados experimentais dos efeitos da adição de um grau de
liberdade (g.d.l.) sobre a manobrabilidade do sistema é apresentado para dois casos: i) dois graus de liberdade, composto de
uma translação e uma rotação e ii) três graus de liberdade, onde
o movimento de pan adiciona uma rotação ao sistema. A plataforma experimental consiste de um robô móvel Nomad 200 com
uma câmera CCD não-calibrada preto-e-branco, montada sobre
um pan-tilt. Uma placa de captura DT-3155 digitaliza e transfere a imagem para a CPU embarcada composta por um Pentium
133 Mhz com 32 Mbytes de memória RAM rodando um sistema
VI Simpósio Brasileiro de Automação Inteligente. Bauru, setembro de 2003
828
operacional Linux.
Na seção 2 o problema a ser resolvido é formalmente definido,
a seção 3 apresenta a solução proposta baseada na abordagem
de controle servo visual bem com as duas matrizes de Jacobiano
do robô utilizadas, na seção 4 são apresentadas as técnicas de
visão computacional usadas para extrair e rastrear os parâmetros
da reta correspondente ao rodapé em tempo real. A validação
experimental encontra-se na seção 5 e a discussão dos resultados
na seção 6.
ρ
y
θ
x
o
2 FORMULAÇÃO DO PROBLEMA
Figura 2: Parametrização da reta.
T
Tc = V Ω
∈ se(3)2 a postura (posição e orientação) e
velocidade (translacional e rotacional) da câmera em relação ao
alvo, respectivamente. Considere uma imagem obtida da câmera
e seja s um vetor de m parâmetros de caracterı́sticas visuais extraı́do a partir dela. Segundo a abordagem proposta por Espiau
et al. (1992), a relação entre a variação do sinal s na imagem com
a velocidade Tc no espaço cartesiano é dada através da chamada
matriz de interação (LT ) definida como:
ṡ =
d
Figura 1: Tarefa servo visual para seguimento de corredores.
O objetivo deste trabalho é a aplicação de controle baseado em
visão utilizando apenas componentes disponı́veis comercialmente. Dentre as possı́veis tarefas realizáveis por visão, escolhemos
a classe dos problemas de seguimento de trajetória utilizando
marcas naturais. Diversas aplicações podem ser encontradas para este tipo de problema, como a inspeção de oleodutos e linhas
de transmissão (Bueno et al., 2002), e na direção de veı́culos em
auto-estradas(Chen and Tsai, 1997). Este trabalho concentrase no uso de marcos naturais em ambientes estruturados e, em
especial, o seguimento da trajetória definida a partir do rodapé
de um corredor. A configuração desejada é tal que o robô deve
manter-se a uma distância determinada d da parede e a câmera
deve permanecer paralelo ao corredor movendo-se a uma velocidade constante A fig. 1 ilustra a trajetória esperada que o robô
realize durante a tarefa. A janela representa a imagem do corredor observada por uma câmera montada sobre o robô.
3 CONTROLE SERVO VISUAL BASEADO
NA IMAGEM
Considere um robô móvel com uma câmera acoplado sobre
ele. Seja T ⊆ SE(3)1 o espaço de trabalho que representa
o espaço de todas as possı́veis configurações espaciais para a
câmera, e n os graus de liberdade do sistema. Seja r̄ ∈ T e
1 SE(3) e
´ a notac¸a˜o para o grupo Euclideano Especial e corresponde ao
espac¸ o de configuraco˜
¸es de corpos rı́gidos (posic¸a˜o e orientac¸a˜o) definido como SE(3) = R3 × SO(3)
∂s dr̄
•
= H • T c = L T Tc ,
∂ r̄ dt
(1)
onde H é o tensor de interação, • é o produto entre dois tensores,
T
Tc = vx vy vz ωx ωy ωz
é o tensor de velocida0 I3
des da câmera e LT = H
a forma matricial do tensor
I3 0
de interação, tal que posto(LT ) = m.
Seja s(r̄(t)) os valores associados à uma certa postura do robô
no instante t. Define-se de forma análoga ao conceito de ligação
rı́gida na mecânica, o conceito de ligação virtual para uma matriz de interação como sendo o conjunto de movimentos T ∗ que
mantém inalterados o sinal de s, ou seja:
ṡ = LT T ∗ = 0.
(2)
Temos que T ∗ ∈ S ∗ onde S ∗ é uma base para o espaço nulo de
LT , N (LT ). A dimensão de S ∗ é chamada de classe da ligação
virtual, dim(S ∗ ) = n − m. Demais informações podem ser
obtidas em (Chaumette et al., 1993).
3.1 Matriz de Interação para Retas
Uma reta no espaço cartesiano tridimensional pode ser descrita
como a intersecção de dois planos:
h1 (x, p1 )
h2 (x, p2 )
= a1 x + b1 y + c 1 z + d 1
= a2 x + b2 y + c 2 z + d 2
=0
.
=0
(3)
Uma representação mı́nima para a projeção da reta no plano
T
imagem é dada pelos parâmetros polares s = θ ρ , tal que:
g(X, P ) = X cos θ + Y sin θ − ρ = 0,
2 se(3)
(4)
e´o espac¸ o tangenteà SE(3)
VI Simpósio Brasileiro de Automação Inteligente. Bauru, setembro de 2003
829
onde (ver Fig. 2):




1
√−c
2
ρ
=
cos θ
=
√ a21
=
√


 sin θ
a1 +b21
(5)
a1 +b21
b1
a21 +b21
cuja matriz de interação demonstrada em (Espiau et al., 1992) é
dada por:
T Lθ
λθ cos θ λθ sin θ −λθ ρ
...
=
LT =
LTρ
λρ cos θ λρ sin θ −λρ ρ
−ρ cos θ
−ρ sin θ
−1
...
(6)
(1 + ρ2 ) sin θ −(1 + ρ2 ) cos θ 0
com
λθ
λρ
=
=
(a2 sin θ − b2 cos θ)/d2
(a2 ρ cos θ + b2 ρ sin θ + c2 )/d2
.
(7)
Para o caso bidimensional T = SE(2) onde o movimento do
robô está limitado ao plano X − Z temos que a matriz de
interação pode ser reduzida a:
λθ cos θ −λθ ρ
−ρ sin θ
T
L =
(8)
λρ cos θ −λρ ρ −(1 + ρ2 ) cos θ
e a base da ligação virtual neste caso é:


−c1 /a1
S∗ =  1 
0
(9)
com λ > 0 obtemos a seguinte expressão para um controlador
de velocidade manipulando as equações (11) e (12):
!
−1
c
c
∂e
∂e
Tc =
−λe −
(13)
∂ r̄
∂t
c
∂e
∂e
∂s
T +c
onde c
∂ r̄ pode ser escolhido como I6 , ∂t = L
∂t (Espiau
c
∂s
et al., 1992) sendo que ∂t representa uma estimativa do movimento próprio do alvo. Freqüentemente é desejável selecionar
mais caracterı́sticas visuais do que o necessário, com o objetivo de acrescentar redundância na tarefa ou evitar singularidades
(Chaumette et al., 1993). Para dim(S ∗ ) 6= 0 procura-se combinar a tarefa servo visual com outra tarefa capaz de controlar
os graus de liberdades livres. A abordagem de tarefa hı́brida
propõe que a função tarefa assuma a forma e = [eT1 , eT2 ]T composta de uma tarefa principal e1 , baseada no sensor, e uma tarefa
T
s
secundária e2 = ∂h
de dimensão n − m expressa como a
∂ r̄
minimização da função de custo hs sob a restrição e1 = 0.
Uma tarefa hı́brida pode ser definida como
e(r̄, t) = W + e1 (r̄, t) + βW ⊥ e2
(14)
onde:
• e1 (r̄(t), t) = C(s − s∗ ) é a tarefa de controle servo visual,
• e2 é uma tarefa secundária definida no espaço nulo de LT ,
que corresponde a uma ligação de classe 1 do tipo prismático. O
movimento livre é uma translação paralela à reta −c1 /a1 x + z.
• W é uma matriz que permite levar em conta mais sensores
que o necessário tal que N (W ) = N (LT )
3.2 Projeto do Controlador
• W ⊥ é o operador de projeção ortogonal no espaço nulo de
W , ou seja, W ⊥ = I − W W + .
A maioria das leis de controle servo visuais baseadas na imagem
calculam os sinais a serem transmitidos aos atuadores através de
uma equação na forma:
Tc = f (C(t), s(r̄(t)), s∗ (t))
(10)
Onde C(t) é uma matriz relacionada à LT , s∗ (t) é a trajetória
desejada para os parâmetros s alcançarem a postura desejada
c é
r̄d , sendo freqüentemente escolhida como sd = s(r̄d ), (·)
o valor estimado, (·)+ é a pseudo-inversa de Moore-Penrose e
f pode ser uma função simples como um ganho proporcional
ou algo mais complexo, como um controle não-linear ou LQG
(Silveira et al., 2002). A abordagem de função tarefa proposta em (Samson et al., 1991) consiste numa forma organizada de
combinar diversos objetivos de controle.
Denomina-se uma função tarefa e(r̄, t) como sendo uma classe
de funções de saı́da associadas à equação de estados do robô que
dependam apenas da postura do robô e da variável tempo. O
problema de controle é expresso através da regulação da função
tarefa, ou seja, uma tarefa é considera completa num intervalo
[0, T ] se e(r̄, t) = 0 para todo t ∈ [0, T ]. Sabendo que
∂e
∂e
ė(r̄, t) =
Tc +
∂ r̄
∂t
(11)
e de modo a obter um comportamento de sistema de primeira
ordem e um decaimento exponencial de e(r, t), isto é
ė = −λe
(12)
• C é uma matriz de combinação e pode ser escolhido como
+
W LT .
• β é número escalar de ponderação.
∂s
Considerando o caso de um alvo sem movimento c
∂t = 0, a
equação (13) torna-se então:
Tc = −λe − βW
⊥
∂e2
∂ r̄
T
,
(15)
onde a função de custo secundária geralmente é definida a priori
e sua forma é portanto conhecida.
3.3 Determinação dos sinais de atuação
Seja Jr o Jacobiano do robô, a matriz que transforma as velocidades dos atuadores do robô, u, para a velocidade do sistema de
coordenadas da câmera. Os sinais transmitido aos atuadores são
calculados invertendo-se a equação Tc = Jr u:
u = Jr+ Tc ,
(16)
onde Tc é dada pela equação (15). O cálculo do Jacobiano do
robô é realizado através da aplicação da relação de transferência
de velocidade através de juntas de revolução, e será ilustrado
para os casos onde o robô de superfı́cie possui dois e três graus
de liberdade.
VI Simpósio Brasileiro de Automação Inteligente. Bauru, setembro de 2003
830
4 ASPECTOS DE VISÃO COMPUTACIONAL
Considere os sistemas de coordenadas do Nomad 200 (Fig. 3)
onde Fb , Ft , Fp e Fc correspondem aos sistemas associados à
base, torre, pan-tilt e a câmera respectivamente, v é a velocidade
de translação da base, na direção zb , θ̇b e θ̇p são as rotações da
base e do pan-tilt nos eixos yb e yp , respectivamente. θp é o
ângulo entre os eixos zt e zp e a altura de Fc em relação ao chão
é h (Fig. 3).
O problema de visão consiste em segmentar da imagem a reta
correspondente ao rodapé esquerdo do corredor e calcular seus
parâmetros ρ e θ em cada uma das imagens capturadas pela
câmera. O problema de rastreamento de caracterı́sticas visuais
envolve duas etapas:
A configuração da base é do tipo synchro-drive. A velocidade lateral é nula, caracterizando a restrição não-holonômica do
sistema. A torre possui uma rotação independente da base, embora neste trabalho consideramos ambos os corpos rigidamente
ligados. O eixo de rotação do pan-tilt está deslocado do eixo de
rotação da base de uma distância dp e o plano imagem da câmera
está distante dc em relação à yp .
Detecção das Caracterı́sticas A segmentação subdivide a imagem em seus objetos constituintes até que os objetos de interesse estejam isolados. As duas propriedades mais usadas
são a similaridade (da intensidade de pixels) onde algoritmos de crescimento, divisão e fusão de regiões são usados,
e a descontinuidade (variação brusca da intensidade) usada
na detecção de linhas e bordas.
·
θp
Fp
yp
xp
Ft
yc
zp
zc Fc
dc
yt
xt
xc
zt
h
θp
· dp
θb
cements
F
·
PSfrag replacements
Fb
x b yb
zb
v
Rastreamento Dependendo das caracterı́sticas usadas, a carga computacional necessária para segmentar e calcular os
parâmetros impede o uso deste esquema dentro do laço de
controle. Uma estratégia muito usada, conhecida como
segmentação em quadro-completo e rastreamento em região-de-interesse, baseia-se no fato de que as caracterı́sticas
geralmente ocupam apenas uma fração do espaço total na
imagem. Inicialmente com o robô parado, a posição das
caracterı́sticas na imagem são determinadas e uma região
ou janela em torno de cada uma delas determinará a partir de então a região onde os filtros serão aplicados. A
atualização da janela é feito considerando-se um movimento lento, usando a posição atual da caracterı́stica como valor
da janela futura. Uma outra alternativa em desenvolvimento
é através de um estimador como filtro de Kalman.
Figura 3: O robô Nomad 200 e seus sistema de coordenadas
associados.
São apresentados a seguir o Jacobiano do robô para os casos considerando e desconsiderando o movimento do pan para a plataforma robótica móvel.
3.4 Controle Servo Visual sem movimento
de pan
Considerando o caso bidimensional, Tc = vx vz ωy sendo
obtido pela equação (15), o controle é dado pela equação (16)
onde:
T
u = v θ̇b
(17)


0 dp + dc
0 
J r = 1
(18)
0
1
(a) Imagem inicial.
(b) Quadro completo.
(c) Janela de interesse em torno
da reta.
3.5 Controle Servo Visual com Movimento
de pan
Figura 4: Processamento de imagem.
T
e,
Neste caso as entradas de controle são u = v θ̇b θ̇p
como demonstrado em (Silveira et al., 2001) o Jacobiano é igual
a:


− sin θp +dp cos θp + dc dc
dp sin θp
0
(19)
Jr =  cos θp
0
1
1
A solução encontrada para detectar o rodapé foi aplicar, na imagem de tons de cinza capturada pela câmera (Fig. 4(a)), um filtro
de Canny (Fig. 4(b)) e em seguida uma transformada de Hough
(retas sobrepostas na Fig. 4(b)) para determinar os parâmetros ρ
e θ da reta. Partindo do pressuposto que o rodapé é o objeto que
projeta na imagem a maior reta, o candidato de maior pontuação
da transformada de Hough é aquela correspondente ao rodapé;
tal suposição é razoável para a maioria dos casos, observou-se
VI Simpósio Brasileiro de Automação Inteligente. Bauru, setembro de 2003
831
1
ρ 2dof (normalizado)
ρ 3dof
θ 2dof (rad)
θ 3dof
0.8
0.6
0.4
0.2
Erro
que, mesmo em casos extremos, quando o rodapé ocupa apenas
uma pequena parcela da imagem, o algoritmo foi capaz de escolher corretamente. Outros fortes candidatos são as linhas geradas
a partir das quinas das paredes e portas, neste caso, descartou-se
os candidatos cuja inclinação encontrava-se entre 90 − e 90 + graus. Como a inclinação de tilt da câmera é zero, o processamento é realizado apenas na metade inferior da imagem e a
janela de interesse em torno da reta foi de 30 pixels (Fig. 4(c)).
0
−0.2
5 RESULTADOS EXPERIMENTAIS
−0.4
O Nomad têm seu movimento restrito ao plano horizontal, ou
T
seja T = R2 × SO(1), Tc = vx vz ωy e, neste caso a
matriz de interação para retas determina uma ligação virtual de
classe 1 do tipo prismático. Dada a tarefa de posicionar a câmera
em relação a um corredor, simbolizado por uma reta extraı́da a
partir do rodapé, a configuração desejada é dada por:
−0.6
−0.8
−1
0
20
40
60
tempo (s)
80
100
120
(a) Variac¸a˜o do erro em ρ e θ para 2 g.d.l. e 3 g.d.l.
• A câmera (Fc ) permanece a uma altura h do chão;
• Fc permanece a uma distância d da parede;
1.5
2dof
3dof
• O eixo z da câmera permanece paralelo à parede.
1
(20)
o que fornece
sd =
−1
tan (−d/h)
θd
=
0
ρd
(21)
Rotação da base (graus/s)
Nesta configuração, a equação da reta é
y+h = 0
h(x, p) =
x−d = 0
0.5
0
−0.5
−1
bT +
=
• A estimativa da matriz de interação é dada por L
+
LT (sd , zbd ),
1 0 0
• A matriz W é escolhida como sendo W =
0 0 1
−1.5
0
20
40
60
Tempo (s)
80
100
120
(b) Velocidade de rotac¸a˜o da base para 2 g.d.l. e 3 g.d.l.
+
• C = W LT |s=sd ,
Figura 5: Resultados Experimentais
• hs = 21 (z(t) − z0 − V t)2 , ou seja
• e2 = 0 z(t) − z0 − V t 0 o que conduz a
2
0 −V 0
• ∂e
∂t =
REFERÊNCIAS
A Fig. 5 compara a progressão do erro das caracterı́sticas visuais para os dois casos apresentados (Eq. (18) e (19)). Observa-se
que a adição de um grau de liberdade melhora a convergência
do parâmetro ρ causando um desacoplamento do erro em θ com
o erro em ρ. Na Fig. 6 pode verificar-se o movimento da base
compensando o movimento do pan-tilt mantendo a câmera alinhada ao corredor.
6 CONCLUSÕES
O sistema mostrou-se robusto com o sistema convergindo mesmo para um tempo de iteração elevado (4 Hz) demonstrando que
o visual-servoing pode ser aplicado mesmo em plataformas obsoletas (Pentium 133 Mhz). Caso taxas mais elevadas sejam necessárias (como no caso de um dirigı́vel robótico) deve-se usar
um processador mais potente ou uma biblioteca otimizada de
processamento de imagem, como o OpenCV da Intel.
Bueno, S. S., Azinheira, J. R., Ramos, J. J. G., Paiva, E. C., Carvalho, J. R. H. and Silveira, G. F. (2002). Project aurora:
Towards autonomous robotic airship, International Conference on Intelligent Robots and Systems.
Chaumette, F., Rives, P. and Espiau, B. (1993). Classification and realization of the different vision-based tasks, in
K. Hashimoto (ed.), Visual Servoing, Vol. 7, World Scientific Series in Robotics and Automated Systems, Singapore,
pp. 199–228.
Chen, K. H. and Tsai, W. H. (1997). Vision-based autonomous
land vehicle guidance in outdoor environments using combined line and road following techniques, Journal of Robotic Systems 14(10): 711–728.
Espiau, B., Chaumette, F. and Rives, P. (1992). A new approach to visual servoing, IEEE Transactions on Robotics and
Automation 8(3): 313–326.
VI Simpósio Brasileiro de Automação Inteligente. Bauru, setembro de 2003
832
Rotação da base e do pan (graus/s)
6
velocidade pan
velocidade base
4
2
0
−2
−4
−6
−8
0
50
100
150
Tempo (s)
Figura 6: Velocidade de rotação da base e do pan para 3 g.d.l.
Samson, C., Borgne, M. L. and Espiau, B. (1991). Robot Control: The Task Function Approach, Oxford Engineering
Science Series. Claderon Press.
Silveira, G. F., Carvalho, J. R. H., Shiroma, P. M., Rives, P. and
Bueno, S. S. (2001). Visual servo control of nonholonomic mobile robots, Proceedings of the 16th Brazilian Congress of Mechanical Engineering, Uberlândia/MG, Brasil,
pp. 333–341.
Silveira, G. F., Carvalho, J. R., Rives, P., Azinheira, J. R., Bueno, S. S. and Madrid, M. K. (2002). Optimal visual servoed
guidance of outdoor autonomous robotic airships, Proceedings of the American Control Conference, USA, pp. 779–
784.
VI Simpósio Brasileiro de Automação Inteligente. Bauru, setembro de 2003
833