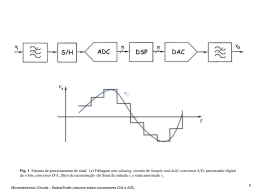
Técnicas de Modelagem e
Controle de Conversores
Estáticos
Prof.: Seleme I. Seleme Jr
DELT - UFMG
12 a 15/10 de 2004
IV INDUSCON – Joinville - SC
Esboço do Curso
Objetivos do Mini-Curso
Obtenção de modelos via Average Switching


Modelling – ASM


Técnicas de Controle




Obtenção dos modelos em Espaço de Estado
Considerações sobre os Modelos
Controle Clássico
Controle Avançado
Conclusões
Objetivos do Mini-Curso




Apresentação de metodologia de modelagem
de conversores.
Obtenção e análise de alguns modelos em
Espaço de Estado.
Apresentação de panorâmica de técnicas de
controle de conversores.
Apresentação de metodologia de projeto de
controladores de conversores.
Obtenção de Modelos via
Average Switching Modelling




Introdução
 Eliminação de ripple de chaveamento
 Supressão de harmônicos
O modelo CA do conversor no Espaço de Estados
O modelo vis-à-vis ao controle
 Representação matemática dos fenômenos físicos
 Modelo simplificado ou “a dinâmica que interessa”
 Insight: “quando, onde e porque”
Exemplos
Introdução

Objetivos dos modelos




(Definição de modelo CA)
A inclusão da dinâmica dominante
Simplicidade, aproximação e precisão
Modelo orientado ao controle
O que é o Modelo CA ?



Aquele que prediz como variações de baixa freqüência na
Razão Cíclica afetam a saída (variável a ser controlada).
Aquele que ignora ripple de chaveamento
Aquele que ignora harmônicos de chaveamento e suas
dinâmicas (quando isto não afeta a sua precisão).
O ripple de chaveamento
Espectro da Tensão de Saída com Modulação
Senoidal da Razão Cíclica
Modelos CC (Steady-state) e modelo CA
Conversor Buck e Filtro LC
Tensão de saída em função de D
Ripple e Tensão CC
Ripple e Tensão CA Média
Conversor Buck-Boost
Introdução

A técnica de obtenção dos Modelos CA



(Obtenção de modelos)
Eliminação dos harmônicos de chaveamento através da
utilização das formas de onda médias em um período de
chaveamento (ASM).
Utilização de modelos lineares (modelagem de pequenos
sinais) das chaves estáticas operando em torno de um ponto
quiescente.
O Modelo CA e os objetivos do controle

Controlar através da Razão Cíclica do conversor a forma de
onda de tensão (corrente) de saída e/ou de entrada, seja ela
CA ou CC, tal que ela siga a referência.
Porque modelo médio (Averaged)?




A representação média de circuito para um conversor chaveado
é útil para a análise, simulação e para se ganhar experiência
sobre a operação do conversor.
É desejável que o circuito (médio) obtido seja o mais fiel
possível do circuito chaveado que o gerou.
Wester e Middlebrook foram pioneiros na utilização da técnica
de síntese de circuitos que eles chamaram de in place ou ainda,
de método direto de obtenção de circuito médio.
Ainda mais interessante do que o modelo de circuito médio do
conversor, é a sua descrição aproximada (pela média) no Espaço
de Estados.
Modelo baseado na média para evitar ripple de
chaveamento

A média num período

Em regime permanente
onde
Obs.: as correntes e tensões
médias são funções não
lineares da Razão Cíclica
Avereging e a eliminação do ripple

A variação média da corrente
do indutor (Buck – Boost)

A variação média no
capacitor (corrente e tensão)
Exemplo de um conversor Buck CC-CC e seu
regulador
Considerações sobre o Modelo CA
de um Conversor




A Hipótese fundamental é de que a variação CA (de
correntes e tensões) é muito menor do que os
valores quiescentes.
As Equações Diferenciais Não Lineares podem,
portanto, ser linearizadas.
A linearização é feita desprezando-se os termos de
segunda ordem e removendo a componente CC (que
soma zero).
O resultado é um modelo linear que descreve a
variação CA de pequenos sinais.
Ponto quiescente, linearização e pequenos sinais
Conversor Buck-Boost
Linearização em torno do ponto quiescente
Eqs. Diferenciais da média (não lineares)
Ponto quiescente e perturbação
Modelo linearizado de pequenos sinais (Buck-Boost)
Equação de Perturbação do Indutor
Desenvolvendo a expressão:
Linearizando:
Modelo linearizado de pequenos sinais (Buck-Boost)
Equação de Perturbação do Capacitor
Desenvolvendo a expressão:
Linearizando:
Não Linearidades do dispositivo e de harmônicos
1. Exemplo de dispositivo não linear (BJT):
Modelo não linear
Modelo linearizado
2. Não linearidades advindas de harmônicos:
Os harmônicos presentes no conversor são responsáveis pelos
termos ≥ 2a. ordem, que aparecem no modelo completo.
O modelo médio no Espaço de Estados



Modelo formal, orientado a aplicações em
controle.
Procedimento generalizado na obtenção dos
modelos descritos por Equações Diferenciais
Lineares Matriciais.
Os modelos de pequenos sinais pela média
são sempre possíveis desde que se disponha
das Eqs. de Estado do conversor original.
Descrição de Sistemas no
Espaço de Estados



Descrição canônica de sistemas dinâmicos por
Sistemas de Equações Diferenciais de primeira
ordem.
Em sistemas lineares, as derivadas das
variáveis de estado podem ser expressas com
combinação linear dos estados e das entradas.
As variáveis de estado são tipicamente de
elementos armazenadores de energia: corrente
em indutor tensão em capacitor, posição e
velocidade de elementos móveis, etc.
Equações de Estado Matriciais de um Sistema
Linear
Forma canônica matricial (sistema linear invariante no tempo)
u(t) – variáveis de entrada (fontes independentes de tensão)
x(t) – variáveis de estado
Y(t) – variáveis de saída (variáveis a serem medidas e controladas)
K – matriz contendo tipicamente valores de capacitância, indutância própria e mútua
A, B, C e E – matrizes de constantes de proporcionalidade
Exemplo com circuito elétrico
Descrição do sistema:
Variáveis de Estado
Matriz K
Vetor de entrada
Variáveis de saída desejadas
Exemplo (Eqs. do circuito)
Obter iC1 via equação nodal:
Obter iC2 via equação nodal:
Obter iC3 via equação de malha:
Exemplo (na forma matricial)
As mesmas equações:
Expressas na forma matricial:
Exemplo (variáveis de saída)
Expresse os elementos do vetor de saída y como combinação linear de x e u
Em forma matricial:
Como Eqs. isoladas:
Modelo de Estados pela média (averaged)

Considere-se que o conversor esteja em condução contínua,
alimentado via Modulação de Largura de Pulsos (PWM)




Existem dois estados e subintervalos associados ao conversor em
cada intervalo de chaveamento.
Em cada subintervalo o conversor tem um comportamento contínuo,
correspondente ao circuito elétrico que o representa e passível de
descrição por Equações de Estado.
As Equações de Estado são lineares por se tratar de modelo
linearizado de pequenos sinais.
As Equações de Estado pela Média (Averaged) são obtidas
pela média das Matrizes de Estado dos 2 subintervalos.
Equações de Estado pela Média
- Hipóteses 
Durante subintervalo 1

As chaves estão em posição
1 e o conversor se reduz a
um circuito passível de ser
descrito por Eqs. de Estado
Lineares:

Durante subintervalo 2

As chaves estão em posição
2 e o conversor se reduz a
um circuito passível de ser
descrito por Eqs. de Estado
Lineares:
Equações de Estado pela Média
- Modelo CC 
SISTEMA EM EQUILÍBRIO (modelo CC) : Na hipótese das freqüências
naturais do conversor e das constantes de tempo das suas variáveis
de entrada serem bem menores do que a freqüência de chaveamento,
o modelo médio do conversor em equilíbrio pode ser descrito por:
As matrizes médias são dadas
como:
Os componentes (CC) em
equilíbrio são:
Vetor de estado (CC)
Vetor de Entrada (CC)
Vetor de Saída (CC)
Razão Cíclica (CC)
Equações de Estado pela Média
- A solução média do sistema em equilíbrio 
A SOLUÇÃO DO SISTEMA EM EQUILÍBRIO: Tendo em vista as
equações médias do sistema linear em equilíbrio, sua solução é:
A solução para X e Y :
Equações de Estado pela Média
- Modelo CA de pequenos sinais (1) 
Algumas definições e explicações:
Note-se que:
Equações de Estado pela Média
- Modelo CA de pequenos sinais (2) 
Dedução Usando-se as definições apresentadas e os sistemas de equação
que representam o sistema dos dois subintervalos, obtém-se:
Equações de Estado pela Média
- Modelo CA de pequenos sinais (3) 
Dedução (cont.) -
1a. ordem CA
termos CC
termos CA de 1a. ordem
termos não lineares de 2a. ordem
CC + 1a. ordem
termos CC
termos CA de 1a. ordem
termos não lineares de 2a. ordem
Equações de Estado pela Média
- Modelo CA de pequenos sinais (4) 
Sempre que for possível descrever os circuitos do conversor nos dois
subintervalos, é possível obter o modelo CA médio de pequenos sinais,
que é um modelo aproximado, desprezando-se os termos de 2a. ordem.
onde:
perturbação de pequeno sinal (CA) no vetor de estado
perturbação de pequeno sinal (CA) no vetor de entrada
perturbação de pequeno sinal (CA) no vetor de saída
perturbação de pequeno sinal (CA) na razão cíclica
Equações de Estado pela Média
- Modelo CA de pequenos sinais (5) 
Sendo que a matriz K é não singular e inversível, pode-se
escrever as Equações de Estado na sua forma mais usual:
Componentes de baixa freqüência das variáveis
de estado e de saída (interpretação gráfica)

Variáveis de estado

Variáveis de saída
Equações de Estado pela Média
- Exemplo com Buck-Boost não ideal (1) Não idealidades do modelo:
• Ron – resistência do MOSFET
conduzindo
• VD – queda de tensão no
diodo
com polarização direta
Vetor de Estados
Vetor de entrada
Vetor de saída
Equações de Estado pela Média
- Exemplo com Buck-Boost não ideal (2) Subintervalo 1 (DTs)
Equações de Estado pela Média
- Exemplo com Buck-Boost não ideal (3) Subintervalo 2 (D’ Ts)
Equações de Estado pela Média
- Exemplo com Buck-Boost não ideal (4) As matrizes médias
de maneira similar:
Equações de Estado pela Média
- Exemplo com Buck-Boost não ideal (5) As Eqs. de Estado CC
A solução CC
Exemplo com Buck-Boost não ideal (6)
- O circuito equivalente CC Eqs. de Estado CC :
Circuito equivalente correspondente:
Exemplo com Buck-Boost não ideal (7)
- O circuito equivalente CA de pequenos sinais Cálculo das matrizes no modelo de pequenos sinais:
Eqs. de Estado CA de pequenos sinais:
Modelagem do Modulador de Largura de
Pulso (PWM) – 1 –

Os moduladores PWM convertem o sinal de referência de tensão,
vc(t), na Razão Cíclica d(t).
Modelagem do Modulador de Largura de
Pulso (PWM) – 2 –

A Razão Cíclica é obtida pela comparação entre a onda dente de
serra com a forma de onde analógica vc(t) que se deseja sintetizar.
Modelagem do Modulador de Largura de
Pulso (PWM) – 3 –

Os moduladores PWM também introduzem amostragem da forma de
onda, embora a referência de tensão, vc(t), seja contínua no tempo.


Existe apenas um valor discreto da Razão Cíclica para cada período de
chaveamento.
O PWM amostra a forma de onda de tensão com a freqüência de chaveamento.
Modelagem do Modulador de Largura de
Pulso (PWM) – 4 –

Alguns cuidados devem ser tomados com relação ao PWM:




Garantir que a banda passante do controlador seja suficientemente
menor do que a freqüência de Nyquist que é fS / 2 .
Evitar que a tensão de referência, vs(t), contenha componentes
harmônicos em torno da freqüência de chaveamento ou maiores.
Tais componentes harmônicos podem ser introduzidos via realimentação.
Variações de alta freqüência em vs(t) podem alterar o comportamento do
PWM, de várias maneiras:





Aparecimento de off-set CC na tensão de saída (em inversores);
Flutuação do tempo de chaveamento com propagação de ruído;
O Fenômeno de aliasing;
Geração de harmônicos indesejáveis;
Ocorrem comportamentos não-lineares não previstos pelo modelo de
pequenos sinais.
Modelagem no Espaço de Estado quando de
elementos (exceto chaves) não lineares


Veremos em seguida, um método alternativo para
contemplar não linearidades no circuito como
elementos resistivos não lineares e elementos
capacitivos e reativos não lineares.
Tais não linearidades ocorrem com capacitores
chaveados, resistores não lineares para descrever
conversores operando em modo descontínuo, etc.
Modelagem no Espaço de Estado (Alternativa) 1
Sistema Linear
d
x  A0 x  B0 w para u  0
dt
d
x  A1 x  B1w para u  1
dt
onde u é o statusda chave (u  1 - chavefechada, u  0 - chaveaberta)
d
x  A0  u ( A1  A0 )x  B0  u ( B1  B0 )w
dt
Sistema não linear
d
x  f 0 ( x, w)  u f1 ( x, w)  f 0 ( x, w)
dt
(formabilinear)
Modelagem no Espaço de Estado (Alternativa) 2
Valores médios
1
x 
T
t
 x(s) ds
t T
1
d (t )  u 
T
t
 u(s) ds
t T
Caso linear :
d
d
x 
x  A0  u ( A1  A0 ) x  B0  u ( B1  B0 ) w
dt
dt
Caso não linear :
d
d
x 
x  f 0 ( x, w)  u f1 ( x, w)  f 0 ( x, w)  f 0 ( x , w )  d  f1 ( x , w )  f 0 ( x , w )
dt
dt
Modelagem no Espaço de Estado (Alternativa) 3
Sendo :
d
x  f 0 ( x0 , w )  ( D  dˆ ) f1 ( x , w )  f 0 ( x , w ) , com d  D  dˆ
dt
linearizando f 0 e f1 em torno de X e W :
f 0  A0 xˆ  B0 wˆ  f 0  X ,W  , f1  A1xˆ  B1wˆ  f1  X ,W  com A  A1D  A0 D
onde : A0 
B0 
obtém - se :


f 0 ( x , w ) x  X ; A1 
f1 ( x , w ) x  X ; xˆ  x  X
 x
 x


f 0 ( x , w ) w  W ; B1 
f1 ( x , w ) w  W ; wˆ  w  W
 w
 w
d
x  Axˆ  Bwˆ  dˆ  f1 ( X ,W )  f 0 ( X ,W )  dˆ  A1  A0 xˆ  B1  B0 wˆ 
dt
Modelagem no Espaço de Estado (Alternativa) 4
Caso linearizado :
d
x  Axˆ  Bwˆ  dˆ  f1 ( X ,W )  f 0 ( X ,W )  dˆ  A1  A0  xˆ  B1  B0  wˆ 
dt
rmo de 2a. ordem
te
onde :
X ,W - caracteriz am o estado do ponto de operação quiescente
xˆ , wˆ e dˆ - caracteriz am variações de pequenos sinais nos estados e na Razão Cíclica
Caso do sistema linear : f 0  A0 x  B0 w e f1  A1 x  B1 w
d
x  Axˆ  Bwˆ  dˆ  A1  A0  X  B1  B0 W   dˆ  A1  A0  xˆ  B1  B0  wˆ 
dt
termode 2a. ordem
Averaging Generalizado 1
(Aplicação a conversores ressonantes)


Metodologia para a modelagem pela média de circuitos chaveados,
generalizada, com precisão estendida de maneira arbitrária a ordens
mais elevadas da série de Fourier.
Método baseado na aproximação de x(n) no intervalo (t-T, t), com
precisão arbitrária:
onde k designa a ordem dos elementos na série de Fourier, s  2 / T ,
é a freqüência de chaveamento, s  (0, T ] , é a variável de tempo no interior
do intervalo. Os coeficientes da série são dados por:
Averaging Generalizado 2

No caso das técnicas estudas até aqui, nós nos contentamos
com usarmos a média da ciclo inteiro T :
que corresponde ao coeficiente CC da série de Fourier do slide
precedente:

Esta aproximação, embora válida para conversores modulados
com PWM a alta freqüência, não é muito boa para conversores
que tenham alguns de seus estados exibindo comportamento
oscilatório, como é o caso dos Conversores Ressonantes.
Averaging Generalizado 3

Propriedade importante do coeficiente da série de Fourier:

Seja o modelo de um circuito chaveado:
onde u(t) é uma função periódica no tempo com período T.

O modelo médio generalizado para o sistema acima fica:
ou seja
Averaging Generalizado 4

Em resumo, o sistema:
é aproximado com precisão arbitrária pela inclusão de termos:
onde a função
Funções de Descrição.

pode ser aproximada usando-se
i) Para o caso de conversores ressonantes, com freqüência
fundamental predominante, basta computar os índices k= 0,
+ 1 e – 1, da série de Fourier. ii) Para os PWM com
chaveamento rápido, basta o índice CC (zero).
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 1

Considere o conversor ressonante série com fonte de tensão:
f r  36 kHz
(freq.ressonância)
f s  38  40 kHz
(freq.da fonte)

O modelo em Espaço de Estados para este conversor tem a forma:
(ondesgn () é a funçãosinal)
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 2

O conversor opera em modo contínuo (fs > fr)
1
 36 kHz
LC
Considere o modelo obtido com, apenas
(freq.ressonância)
fr 
f s  38  40kHz
(freq.da fonte)

os seguintes coeficientes da série de
Fourier: i 1 , i 1 , v 1 e v 1
O modelo em Espaço de Estados tem, então, a seguinte forma:
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 3

O modelo para a componente fundamental resulta de 4a. ordem (duas
equações para +1 e duas para –1)
Sabendo-se que:

O modelo em Espaço de Estados tem, então, a seguinte forma:

s e Vs podem ser consideradas como entradas externas a este modelo.
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 4

Note que
Comparação entre as forma de onda de corrente e tensão e as
componentes de ordem 1:
são as envoltórias de i(t) e v(t) , pelo modelo apresentado.
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 5

Seja o conversor ressonante série mais realista da figura:
As Equações diferenciais que descrevem
A dinâmica do conversor:
(ondesgn () é a funçãosinal)

Fazendo-se a aproximação pelos harmônicos fundamentais de primeira
ordem:
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 6

Os termos não lineares das
Equações Diferenciais anteriores
ficam:

As Equações Diferenciais de
primeira harmônica ficam:
Modelagem de um Conversor Ressonante
(Exemplo de aplicação) 7

Solução em Regime Permanente
componentes harmônicos da corrente
módulo da corrente
freqüência de
operação
tensão no capacitor
do filtro
componentes harmônicos da tensão
Os termos maiúsculos
denotam operação em
Regime Permanente
Modelagem de um Inversor Trifásico
(Exemplo de aplicação)





Os inversores são conversores CC-CA com Modulação de largura
de Pulso.
Eles são largamente utilizados em aplicações de acionamento
CA e em fontes ininterruptas de potência (UPS).
Métodos de Averaging são empregados para a obtenção de
modelos em tempo contínuo.
A diferença fundamental no caso de inversores (com relação aos
conversores CC-CC) é que se deseja uma tensão de saída
senoidal.
Veja a seguir, um sumário da modelagem de inversores
trifásicos.
Modelagem de um Inversor Trifásico 1

O conceito do chaveamento PWM

Circuitos de chaveamento
Qdo Vsin>Vtri a chave fecha
Qdo Vsin>Vtri a chave abre
Modelagem de um Inversor Trifásico 2
Componente fundamental
PWM trifásico
harmônicos
Modelagem de um Inversor Trifásico 3
O inversor trifásico
2
As equações
2
2
S1* , S2* e S3* são as funções de chaveamento
relativas às fases A, B e C
Modelagem de um Inversor Trifásico 4
As funçõesde chaveamento S1* , S2* e S3* são variáveisdiscretas.
Elas podemser aproximadas por seus valoresmédios no tempo:
- razão de modulação
- defasagem angular
• Observe que, na Equação acima, está representada apenas a
componente fundamental da tensão média equivalente.
• Neste caso, as funções de chaveamento podem ser encaradas
como tensões de entrada.
Modelagem de um Inversor Trifásico 5
As Eqs. do sistema trifásico no Espaço
de Estados
Variáveis de Estado
Variáveis de Entrada
Modelagem de um Inversor Trifásico 6
O processode Averagingtransforma as variáveisdiscretas
de chaveamento, Si* , em sinais de modulaçãocontínuos, u.
Variáveis de Estado
Variáveis de Entrada contínuas, obtidas pelo
valor médio das funções de chaveamento Si*.
Modelagem de um Inversor Trifásico 7
A transformação trifásico – bifásica
Variáveis no sistema
de coordenadas dq0
Matrizes de transformação
Modelagem de um Inversor Trifásico 8
As Eqs. de Estado no referencial girante dq0
As Equações de Estado
A Matriz de Estado
As variáveis de estado
As variáveis de entrada
Modelagem de um Inversor Trifásico 9
As Eqs. de Estado em dq0 para o sistema equilibrado
• d e q indicam componentes de
eixo direto e em quadratura e
0 indica as componentes de
seqüência zero do sistema.
• para o sistema equilibrado,
as componentes de seqüência
zero são desacopladas do resto
do sistema e podem ser removidas.
• com isto, obtém-se um sistema
de ordem reduzida (6a. ordem)
invariante no tempo.
O modelo vis-a-vis do controle – 1 –
- Comentários




Para o controle, o modelo deve ser sempre o mais simples
possível.
Entende-se possível como aquele que, a despeito da sua
simplicidade, retém o que é essencial para os objetivos de
controle almejados.
Deve-se buscar a síntese de modelos compatíveis com a lei de
controle empregada.
Os métodos de obtenção de modelos médios (averaged) no
Espaço de Estados são, do ponto de vista do controle, os mais
indicados.
O modelo vis-a-vis do controle – 2 –
- Comentários

Alguns cuidados devem ser observados quanto ao modelo para o
controle:

O conversor em malha fechada pode ter comportamentos dinâmicos
distintos da operação em malha aberta.




Inversores controlados em corrente apresentam comportamentos não lineares.
Leis de controle não linear (a estrutura variável por modos deslizantes, por
exemplo).
Certos conversores requerem aproximações mais finas: os conversores
ressonantes podem requerer a incorporação de termos de segunda ordem
na aproximação.
Modelos em tempo discreto são, em geral, interessantes para aplicações em
controle de conversores pela sua natureza mesma (cíclica, chaveada).
O modelo vis-a-vis do controle – 3 –
- Representação matemática dos fenômenos físicos

Vimos até aqui técnicas para descrever os conversores sob a forma de
sistemas dinâmicos descritos no Espaço de Estados.


Vimos aspectos relevantes dos sistemas chaveados e como harmônicos e
oscilações de corrente e tensão.
Vimos como obter equivalentes contínuos de sistemas chaveados:




Modelando os conversores pelo comportamento médio num período.
Linearizando os elementos não lineares e deduzindo modelos no Espaço de
Estados para pequenos sinais em torno do ponto de operação
Estudamos técnicas de modelagem de conversores onde a aproximação de
primeira ordem não é suficiente: os conversores ressonantes podem
requerer a incorporação de termos de segunda ordem na aproximação.
Vários exemplos foram apresentados da obtenção destes modelos.
O modelo vis-a-vis do controle – 4 –
- Modelo simplificado ou “a dinâmica que interessa”



Os modelos estudados foram simplificados em vários aspectos,
sempre que possível. Reteve-se o que era essencial no modelo,
tendo em conta a sua aplicação em controle e simulação numérica.
Os modelos são elaborados em função da aplicação que visam,
além das suas características inerentes.
Técnicas que ajudam na decisão pelo melhor modelo de conversor:
i) Funções de Descrição, aproximando por harmônicas
modelos complexos de circuitos chaveados;
ii) Teoria das Perturbações e aproximações pela média;
iii) Modelos linearizados de pequenos sinais;
O modelo vis-a-vis do controle – 5 –
- Insights




A partir daqui, os aprimoramentos dos modelos vêm junto com a
técnica de controle escolhida para o conversor.
Discutiremos, na parte final deste mini-curso, alguns aspectos
relevantes e alguns exemplos de controle de conversores estáticos.
A abordagem buscada aqui é sempre no sentido da aproximação
das técnicas de controle e da modelagem do conversor.
Não se pretende aqui apresentar técnicas ou resultados novos de
controle de conversores. O foco é a modelagem.
Técnicas de Controle de Conversores


O primeiro passo para fazer o controle eficiente do conversor já foi
dado: obter de forma apropriada o seu modelo em Espaço de
Estados.
Em muitos casos é apropriado utilizar-se o modelo em tempo
discreto ou modelo de sinais amostrados.


Sendo o conversor na sua essência um circuito discreto (chaveado)
com freqüência de chaveamento controlada, é natural utilizar-se
períodos de amostragem do modelo em tempo discreto intimamente
relacionados com esta freqüência (igual ou múltiplo).
De posse do modelo no Espaço de Estados (discreto ou contínuo)
o projeto do controlador um um procedimento corrente na teoria
de controle.
Técnicas de Controle de Conversores
- Modelo amostrado 1

A partir de modelos contínuos, obtidos pelas técnicas apresentadas
anteriormente, dispõe-se de ferramentas numéricas para a obtenção do
modelo discreto. Exemplo:
dx
 Ax(t )  Bu(t )
dt
y (t )  Cx (t )  Du(t )
Modelo em
tempocontínuo
Obtém-se o modelo amostrado como:
x[k  1]  A x[k ]  B u[k]
Modelo amostrado
y[k] Cx[k ]  Du[k ]
T
onde : A  e
AT
, B   e A(T-  ) B d , C  C , D  D
0
com T  períodode amostragem
Técnicas de Controle de Conversores
- Modelo amostrado 2

Seja o modelo contínuo, linear e invariante no tempo:
dx
 Ax(t )  Bu(t )
dt
y (t )  Cx (t )  Du(t )
 2 -1
A   1 0
 3 - 3
3
1
2 ; B   0
 0
1 
0
1  ; C  1 0 0
0

e D0
Obtém-se o modelo amostrado como:
x[k  1]  A x[k ]  B u[k]
y[k] Cx[k ]  Du[k ]
onde :
1.0002 - 0.0001 0.0003
 1.000 0.000
A  0.0001 1.0000 0.0002 , B  10 4  0.000 1.000 , C  C , D  D
0.0003 - 0.0003 1.0001
 0.000 0.000
com T  10 4
Técnicas de Controle de Conversores
- Modelo amostrado 3

Note que se aproximássemos:
x
 Ax(t )  Bu(t )
t
y (t )  Cx (t )  Du(t )
x(k  1)  I  AT x(k )  BTu(k )
y(k  1)  Cx(k )  Du(k )
com x(k  1 )  x(k) x e t  T
Neste caso, as matrizes são as mesmas até, pelo menos, a 4a. casa decimal:
A  I  AT , B  BT
1.0002 - 0.0001 0.0003
 1.000 0.000
A  0.0001 1.0000 0.0002 , B  10 4  0.000 1.000 , C  C , D  D
0.0003 - 0.0003 1.0001
 0.000 0.000
com T  10 4
Técnicas de Controle de Conversores
- Modelo amostrado 4
- Considere agora um sistema não linear:
dx
 f ( x(t ),u (t ))
dt
y (t )  g ( x(t ),u (t ))
Alguns cuidados especiais devem ser tomados na discretização destes sistemas:




Sistemas não lineares costumas expandir a largura de banda de suas entradas.
Portanto, a escolha da freqüência de amostragem é importante para evitar-se,
entre outras coisas, o fenômeno de aliasing.
Admitindo-se certas condições às não linearidades (deriváveis, sem memória, etc.)
é possível obter-se modelos simples, desde que a freqüência de amostragem seja
grande o suficiente.
Tomando-se os cuidados acima, podemos aproximar o modelo amostrado por:
x(k  1)  x(k )  f ( x(k ),u (k ))T
y(k )  g ( x(k ),u (k ))
Técnicas de Controle de Conversores
- Modelo amostrado 5 (Exemplo)
- Veja o exemplo de duas situações de amostragem e síntese do PWM:
A amostragem se dá sempre no meio do pulso, para minimizar os efeitos de transitório
A atualização se dá
no fim do ciclo
1 - A freqüência de amostragem é a mesma do
chaveamento do PWM
2 - A atualização de Vc se dá uma vez por ciclo
A atualização se dá
no instante da amostragem
1 - A freqüência de amostragem é o dobro do
chaveamento do PWM
2 - A atualização de Vc se dá em dois instantes
de amostragem por ciclo
Técnicas de Controle de Conversores
- Controle Clássico e Controle Avançado

Controle Clássico: aplica-se a sistemas lineares (ou linearizados),
utilizando-se de ferramentas do domínio da freqüência aplicadas
funções de transferência:




Para estabelecer a robustez: margens de fase e de ganho.
Para estabelecer a resposta dinâmica, o parâmetro é a banda passante, a
freqüência de corte, associadas com a alocação dos pólos do sistema em
malha fechada.
A vantagem desta abordagem reside na maturidade das técnicas de
projeto, nos inúmeros exemplos disponíveis e na simplicidade na
interpretação física do sistema.
Aspectos, como o da rejeição a perturbações, são bastante bem
caracterizados pelo controle no domínio da freqüência e, sobretudo,
existe uma familiaridade e boa aceitação deste tipo de controle no meio
industrial.
Técnicas de Controle de Conversores

Estratégias simples


Controle on-off : trata-se de controladores do tipo “liga-desliga” usado
principalmente nas malhas de corrente através da comparação do erro de
corrente (comparador e sample and hold); a freqüência de chaveamento é
variável.
Controle de histerese: traz melhoria ao esquema acima através da modulação
do sinal do erro por uma portadora triangular de freqüência definida e
submetido a um comparador de histerese;



o resultado é uma modulação PWM senoidal de conteúdo harmônico bem definido;
A desvantagem é não alcançar atracamento perfeito à referência.
Controlador PI: nesta estratégia simples e largamente utilizada, a referência
para o PWM senoidal é a soma do erro multiplicado por um ganho
(proporcional) e a sua integral, multiplicada por seu ganho (integral).
Técnicas de Controle de Conversores
- Controle Avançado – Espaço de Estados

Controle no Espaço de Estados: aplica-se a sistemas tanto lineares
quanto não lineares; Existem várias técnicas de projeto de controladores
baseados no modelo de Espaço de Estados:



O mais geral é o controle por realimentação estática de estados e alocação
de pólos.
 Para sistemas não lineares passíveis de linearização por realimentação de
estados, as técnicas usuais de alocação de pólos também se aplicam.
Dada a natureza dos conversores de potência, inerentemente amostrados, é
comum se trabalhar com o modelo discretizado das Equações de Estado.
 Neste bojo, controladores dead-beat, de estrutura variável, dentre outros,
são largamente utilizados.
Técnicas de controle avançado vêm sendo bastante empregadas para
responder a problemas específicas da planta.

controle adaptativo, controle robusto, etc;

o controle repetitivo associado com outros.
Técnicas de Controle de Conversores
- Controle Avançado – Exemplos

Veremos, a seguir, alguns exemplos de controladores (em simulação)
aplicados a uma UPS (Uninterruptable Power Source).



Controle por realimentação de estado e alocação de pólos.
 Sem compensação de atraso.
 Com compensação de atraso.
Controle Deadbeat.
 Sem compensação de atraso.
 Com compensação de atraso.
Controle repetitivo adicional.
Bibliografia
LIVROS:
1. Power Electronics Converters, Application and Design - Moham, N. T., M
Undeland and W.P. Robbins – John Wiley, New York.
2. Fundamentals of Power Electronics – Erikson, R. W., Ed. Chapman & Hall, 1997.
3. Principles of Power Electronics – Kassakian, J. G., Schlecht, M. F e Verghese, G.
C. - Addison – Wesley Publishing Co., 1991.
4. Power Electronics and Variable Frequency Drives Technology and Application –
Bismal K. Bose – IEEE Press.
Bibliografia
Artigos em periódicos e revistas sobre os tópicos do curso:
1. S. R. Sanders, J. M. Noworolski, X. Z. Liu e G. Verghese, Generalized Averaging Method for
Power Conversion Circuits, IEEE Trans. On Power Elecronics, vol. 6, no. 2, pp. 251- 259,
Abril 1991.
2. E. X. Yang, F. C. Lee e M. M. Janovic, Small Signal Modeling of Series and Parallel Resonant
Converters, Power Electronics Specialists Conference, 1992. PESC '92 Record., 23rd Annual
IEEE , 29 June-3 July 1992; Pages:941 - 948 vol.2
3. Krein, P.T.; Bentsman, J.; Bass, R.M.; Lesieutre, B.L., On the use of averaging for the analysis of
power electronic systems, Power Electronics, IEEE Transactions on, Volume: 5 , Issue: 2 ,
April 1990, Pages:182 - 190
4. Witulski, A.F.; Erickson, R.W.; Extension of state-space averaging to resonant switches and
beyond; Power Electronics, IEEE Transactions on ,Volume: 5 , Issue: 1 , Jan. 1990 Pages:98
– 109
5. Sanders, S.R.; Verghese, G.C.; Synthesis of averaged circuit models for switched power converter;
Circuits and Systems, IEEE Transactions on ,Volume: 38 , Issue: 8 , Aug. 1991, Pages:905 –
915.
6. Forsyth, A.J.; Ho, Y.K.E.; Ong, H.M.; Comparison of small-signal modelling techniques for the
series-parallel resonant converter; Power Electronics and Variable-Speed Drives, 1994. Fifth
International Conference on , 26-28 Oct 1994, Pages:268 - 273