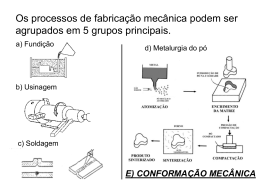
Universidade Federal do Paraná
Setor de Tecnologia
Depto de Engenharia Química
Prof. Dr. Mário José Dallavalli
BIOMATERIAIS E BIOMECÂNICA
TQ-064
Biomateriais Metálicos
PROPRIEDADES MECÂNICAS
Propriedades Mecânicas
de Metais
 Como os metais são materiais estruturais, o
conhecimento de suas propriedades mecânicas
é fundamental para sua aplicação.
 Um grande número de propriedades pode ser
derivado de um único tipo de experimento, o
teste de tração.
 Neste tipo de teste um material é tracionado e se
deforma até fraturar. Mede-se o valor da força e
do elongamento a cada instante, e gera-se uma
curva tensão-deformação.
Curva Tensão-Deformação
Célula de Carga
Carga (103N)
100
50
0
0
Amostra
500
Tensão,  (MPa)
Gage
Length
Tração
5
Normalização para
eliminar influência
da geometria da
amostra
250
0
1
2
3
4
Elongamento (mm)
0
0.02 0.04 0.05 0.08
Deformação,  (mm/mm)
0.10

Curva Tensão-Deformação
(cont.)
Normalização
–  = P/A0 onde P é a carga e A0 é a seção reta da amostra
–  = (L-L0)/L0 onde L é o comprimento para uma dada carga e
L0 é o comprimento original
 A curva  pode ser dividida em duas regiões.
– Região elástica
  é proporcional a  => =EE=módulo de Young
 A deformação é reversível.
 Ligações atômicas são alongadas mas não se rompem.
– Região plástica
  não é linearmente proporcional a .
 A deformação é quase toda não reversível.
 Ligações atômicas são alongadas e se rompem.
Curva Tensão-Deformação
(cont.)
Elástica
Tensão,  (MPa)
500
Limite de escoamento
Plástica
250
fratura

0
0
0.02
0.04
0.05
0.08
Deformação,  (mm/mm)
O Módulo de Young, E, (ou módulo de
elasticidade) é dado pela derivada da
curva na região linear.
0.002 0.004 0.005 0.008 0.010
Deformação,  (mm/mm)
Como não existe um limite claro entre as regiões
elástica e plástica, define-se o Limite de
escoamento, como a tensão que, após liberada,
causa uma pequena deformação residual de
0.2%.
0.10
0
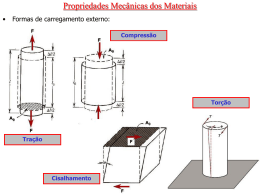
Cisalhamento
 Uma tensão cisalhante causa uma deformação
cisalhante, de forma análoga a uma tração.
– Tensão cisalhante
  = F/A0
 onde A0 é a área paralela a
aplicação da força.
– Deformação cisalhante
 = tan = y/z0
 onde  é o ângulo de
deformação
 Módulo de cisalhamento G
  = G 
Coeficiente de Poisson
 Quando ocorre elongamento ao longo de
uma direção, ocorre contração no plano
perpendicular.
 A Relação entre as deformações é dada
pelo coeficiente de Poisson .
 = - x / z = - y / z
– o sinal negativo apenas indica que uma
extensão gera uma contração e viceversa
– Os valores de  para diversos metais
estão entre
0.25 e 0.35.
E = 2G(1+)
Estricção e limite de
resistência
Tensão, 
Limite de
resistência
estricção
A partir do limite de
resistência começa a ocorrer
um estricção no corpo de
prova. A tensão se
concentra nesta região,
levando à fratura.
Deformação, 
Ductilidade
 Ductilidade é uma medida da extensão da
deformação que ocorre até a fratura.
 Ductilidade pode ser definida como
– Elongamento percentual %EL = 100 x (Lf - L0)/L0
 onde Lf é o elongamento na fratura
 uma fração substancial da deformação se concentra na
estricção, o que faz com que %EL dependa do comprimento
do corpo de prova. Assim o valor de L0 deve ser citado.
– Redução de área percentual %AR = 100 x(A0 - Af)/A0
 onde A0 e Af se referem à área da seção reta original e na
fratura.
 Independente de A0 e L0 e em geral  de EL%
Resiliência
 Resiliência é a capacidade que o material possui de
absorver energia elástica sob tração e devolvê-la
quando relaxado.
– área sob a curva dada pelo limite de escoamento e
pela deformação no escoamento.
– Módulo de resiliência Ur = d com limites de 0 a
y
– Na região linear Ur =yy /2 =y(y /E)/2 = y2/2E
– Assim, materiais de alta resiliência possuem alto
limite de escoamento e baixo módulo de
elasticidade.
– Estes materiais seriam ideais para uso em molas.
Tenacidade
 Tenacidade (toughness) é a capacidade que o material
possui de absorver energia mecânica até a fratura.
– área sob a curva  até a fratura.
Frágil
Tensão, 
Dúctil
O material frágil tem maior
limite de escoamento e maior
limite de resistência. No entanto,
tem menor tenacidade devido a
falta de ductilidade (a área sob a
curva correspondente é muito
menor).
Deformação, 
Resumo da curva  e
propriedades
– Região elástica (deformação reversível) e região plástica
(deformação quase toda irreversível).
– Módulo de Young ou módulo de elasticidade => derivada da
curva na região elástica (linear).
– Limite de escoamento (yield strength) => define a transição
entre região elástica e plástica => tensão que, liberada, gera
uma deformação residual de 0.2%.
– Limite de resistência (tensile strength) => tensão máxima
na curva  de engenharia.
– Ductilidade => medida da deformabilidade do material
– Resiliência => medida da capacidade de absorver e devolver
energia mecânica => área sob a região linear.
– Tenacidade (toughness) => medida da capacidade de
absorver energia mecânica até a fratura=> área sob a curva
até a fratura.
A curva  real
fratura
– A curva  obtida experimentalmente é
denominada curva  de engenharia.
 Esta curva passa por um máximo de
tensão, parecendo indicar que, a partir
deste valor, o material se torna mais
fraco, o que não é verdade.
 Isto, na verdade, é uma consequência
da estricção, que concentra o esforço
numa área menor.
– Pode-se corrigir este efeito levando em
conta a diminuição de área, gerando
assim a curva real.
curva  real
curva  de engenharia
fratura
Sistemas de deslizamento
(rev.)
Estrutura
Cristalin
a
Planos de
Deslizamento
Direções de
Deslizamento
Número de
Sistemas de
Deslizamento
CCC
{110}
{211}
{321}
<111>
6x2 = 12
12
24
-Fe, Mo,
W
CFC
{111}
<110>
4x3 = 12
Al, Cu,
-Fe, Ni
<1120>
3
3
6
Cd, Mg,
-Ti, Zn
HC
{0001}
{1010}
{1011}
Geometria da
Célula
Unitária
Exemplo
s
A tabela mostra os sistemas de deslizamento das 3 redes básicas. Em branco aparecem os
sistemas principais. Em cinza aparecem os secundários. Por exemplo: Como a rede CFC tem 4
vezes mais sistemas primários que a HC, ela será muito mais dúctil.
Deslizamento em monocristais
 A aplicação de tração ou compressão uniaxais
trará componentes de cisalhamento em planos
e direções que não sejam paralelos ou normais
ao eixo de aplicação da tensão.
 Isto explica a relação entre a curva  e a
resposta mecânica de discordâncias, que só se
movem sob a aplicação de tensões
cisalhantes.
 Para estabelecer numericamente a relação
entre tração (ou compressão) e tensão
cisalhante, deve-se projetar a tração (ou
compressão) no plano e direção de
deslizamento.
Tensão cisalhante resolvida
F
Plano de
deslizamento
Direção de
deslizamento
– O sistema de deslizamento
que sofrer a maior R, será
o primeiro a operar.
R =  cos  cos  – A deformação plástica
começa a ocorrer quando a
onde
tração excede a tensão
 = F/A
cisalhante resolvida
crítica (CRSS - critical
resolved shear stress).
F
Deformação plástica em materiais
policristalinos
 A deformação em materiais policristalinos é mais
complexa porque diferentes grãos estarão
orientados diferentemente em relação a direção
de aplicação da tensão.
 Além disso, os grãos estão unidos por fronteiras
de grão que se mantém íntegras, o que coloca
mais restrições a deformação de cada grão.
 Materiais policristalinos são mais resistentes do
que seus mono-cristais, exigindo maiores
tensões para gerar deformação plástica.
Mecanismos de Aumento de
Resistência
 A deformação plástica depende diretamente do
movimento das discordâncias. Quanto maior a
facilidade de movimento, menos resistente é o
material.
 Para aumentar a resistência, procura-se
restringir o movimento das discordâncias. Os
mecanismos básicos para isso são:
– Redução de tamanho de grão
– Solução sólida
– Deformação a frio (encruamento, trabalho a
frio)
Redução de tamanho de grão
 As fronteiras de grão funcionam como barreiras para o
movimento de discordâncias. Isto porque:
– Ao passar de um grão com uma certa orientação para outro
com orientação muito diferente (fronteiras de alto ângulo) a
discordância tem que mudar de direção, o que envolve
muitas distorções locais na rede cristalina.
– A fronteira é uma região desordenada, o que faz com que os
planos de deslizamento sofram descontinuidades.
 Como um material com grãos menores tem mais fronteiras de
grão, ele será mais resistente.
Redução de tamanho de grão
(cont.)
Latão
(70Cu-30Zn)
d-1/2 (mm-1/2)
Limite de escoamento (MPa)
– onde 0 e ky são
constantes para um
dado material
d (mm)
Limite de escoamento (kpsi)
 Para muitos materiais,
é possível encontrar
uma relação entre o
limite de escoamento,
y, e o tamanho médio
de grão, d.
y = 0 + kyd-1/2
Solução sólida
Liga Cu-Zn
Concentração de Zn (%)
Limite de resistência (MPa)
Limite de resistência (kpsi)
 Nesta técnica, a presença de impurezas substitucionais ou
intersticiais leva a um aumento da resistência do material.
Metais ultra puros são sempre mais macios e fracos do que
suas ligas.
Deformação a frio
 O aumento de resistência por deformação
mecânica (strain hardening) ocorre porque:
– o número de discordâncias aumenta com a
deformação
– isto causa maior interação entre as discordâncias
– o que, por sua vez, dificulta o movimento das
discordâncias, aumentando a resistência.
 Como este tipo de deformação se dá a
temperaturas muito abaixo da temperatura de
fusão, costuma-se denominar este método
deformação a frio (cold work).
Deformação a frio (cont.)
%CW=100x(A0-Ad)/A0
Cobre
% Trabalho a frio (%CW)
Ductilidade (%EL)
Latão
Limite de escoamento (MPa)
Limite de escoamento (kpsi)
Aço 1040
Latão
Cobre
Aço
1040
% Trabalho a frio (%CW)
Recuperação e Recristalização
 Como já vimos, a deformação plástica de materiais a
baixas temperaturas causa mudanças microestruturais e
de propriedades.
 Estes efeitos podem ser revertidos, e as propriedades
restauradas, através de tratamentos térmicos a altas
temperaturas.
 Os dois processos básicos para que isto ocorra são
– Recuperação - uma parte das deformações
acumuladas é eliminada através do movimento de
discordâncias, facilitado por maior difusão a altas
temperaturas.
– Recristalização - formação de novos grãos, não
deformados, que crescem até substituir
completamente o material original.
Crescimento de grão
 Como os contornos de grão são regiões
deformadas do material, existe uma energia
mecânica associada a eles.
 O crescimento de grãos ocorre porque desta
forma a área total de contornos se reduz,
reduzindo a energia mecânica associada.
 No crescimento de grão, grãos grandes crescem
às expensas de grãos pequenos que diminuem.
Desta forma o tamanho médio de grão aumenta
com o tempo.
Crescimento de grão (cont.)
dn - d0n =Kt
– onde d0 é o diâmetro
original (t=0)
– K e n são constantes e
em geral n2
Diâmetro de grão (mm)
 Para muitos materiais
poli-cristalinos vale a
seguinte relação para
o diâmetro médio de
grão d, em função do
tempo t.
Tempo (min)
Fim
Até a próxima aula