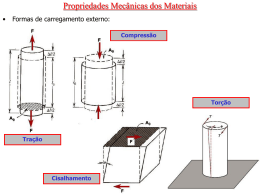
Resistência dos Materiais
Resistência dos Materiais
Relação entre Tensões e Deformações
Resistência dos Materiais
Propriedades Mecânicas dos Metais
•
Um grande número de propriedades pode ser derivado de um único tipo de
ensaio, o ensaio de tração.
No ensaio de tração, um material é tracionado e deforma-se até a ruptura.
Mede-se o valor da força e do alongamento a cada instante, e gera-se uma
curva tensão-deformação.
Resistência dos Materiais
Tensão e Deformação
P
   Tensão Norm al
A


L
 Deform ação


2P P

2A A

L
P
A
2 


2L L

Resistência dos Materiais
Carga (103 N)
Diagrama Tensão - Extensão
Célula de Carga
100
50
0
0
1
2
3
4
5
Alongamento (mm)
corpo de prova
Tensão,  (MPa)
500
Tração
Normalização para
eliminar influência da
geometria da amostra
250
0
0
0.02 0.04 0.05
0.08
Deformação,  (mm/mm)
0.10
Resistência dos Materiais
Curva Tensão - Deformação
•
Normalização
  = P/A0 onde P é a carga e A0 é a área da seção reta do corpo de prova.
  = (L-L0)/L0 onde L é o comprimento para uma dada carga e L0 é o comprimento original
•
A curva  -  pode ser dividida em duas regiões:
 Região elástica
  é proporcional a  =>  = E. onde E = módulo de Young
 A deformação é reversível.
 Ligações atômicas são alongadas mas não se rompem.
 Região plástica
  não é linearmente proporcional a .
 A deformação é quase toda não reversível.
 Ligações atômicas são alongadas e rompem-se.
Resistência dos Materiais
Curva Tensão – Deformação
Elástica
Tensão, σ (MPa)
500
Limite de escoamento
Plástica
250
Fratura
0
0
0.02
0.04
0.05
0.08
Deformação, ε (mm/mm)
O Módulo de Young, E, (ou módulo de
elasticidade) é dado pela derivada da curva na
região linear.
0.10

0
0.002 0.004 0.005 0.008 0.010
Deformação,  (mm/mm)
Como não existe um limite claro entre as regiões
elástica e plástica, define-se o limite de escoamento,
como a tensão que, após a libertação da carga, causa
uma pequena deformação residual de 0.2%.
Resistência dos Materiais
Diagrama Tensão x Deformação: Materiais Dúcteis
Resistência dos Materiais
Diagrama Tensão - Deformação: Materiais Frágeis
Resistência dos Materiais
Módulo de Elasticidade ou Módulo de Young
Lei de Hooke:
=E
Resistência dos Materiais
Estricção e limite de resistência
Tensão, 
Limite de
resistência
Estricção
A partir do limite de resistência
começa a ocorrer uma estricção no
corpo de prova. A tensão concentra-se
nesta região, levando à ruptura.
Deformação, 
Resistência dos Materiais
Fratura dúctil e frágil
• Fratura dúctil
 o material deforma-se substancialmente antes de fraturar.
 O processo desenvolve-se de forma relativamente lenta à medida que a fenda se
propaga.
 Este tipo de fenda é denominado estável porque ela para de se propagar a
menos que haja uma aumento da tensão aplicada no material.
Resistência dos Materiais
Fratura
Fratura frágil
 O material deforma-se pouco, antes de fraturar.
 O processo de propagação da fenda pode ser muito veloz, gerando situações
catastróficas.
 A partir de um certo ponto, a fenda é dita instável porque se propagará mesmo
sem aumento da tensão aplicada sobre o material.
Resistência dos Materiais
Ductilidade
• Ductilidade é uma medida da extensão da deformação que ocorre até a fratura.
• Ductilidade pode ser definida como:
 Alongamento percentual % AL = 100 x (Lf - L0)/L0
 onde Lf é o alongamento na fratura
 uma fração substancial da deformação concentra-se na estricção, o que faz com
que a % AL dependa do comprimento do provete. Assim o valor de L0 deve ser
citado.
 Redução de área percentual %AR = 100 x(A0 - Af)/A0
 onde A0 e Af se referem à área da secção recta original e na fractura.
 Independente de A0 e L0 e em geral  de AL%
Resistência dos Materiais
Resiliência
• Resiliência é a capacidade que o material possui de absorver energia elástica
sob tração e devolvê-la quando relaxado.
 Área sob a curva dada pelo limite de escoamento e pela extensão no
escoamento.
 Módulo de resiliência Ur =   d com limites de 0 a y
 Na região linear Ur =yy /2 =y(y /E)/2 = y2/2E
 Assim, materiais de alta resiliência possuem alto limite de escoamento e
baixo módulo de elasticidade.
 Estes materiais seriam ideais para uso em molas.
14
Resistência dos Materiais
Tenacidade
• Tenacidade (toughness) é a capacidade que o material possui de absorver energia
mecânica até a fratura.
Área sob a curva - até a fratura
Frágil
Dúctil
Tensão, 
O material frágil tem maior tensão de
escoamento
e
maior
tensão
de
resistência. No entanto, tem menor
tenacidade devido à falta de ductilidade
(a área sob a curva correspondente é
muito menor).
Extensão, 
Resistência dos Materiais
Resumo da curva - e Propriedades
 Região elástica (deformação reversível) e região plástica (deformação quase toda
irreversível).
 Módulo de Young ou módulo de elasticidade => derivada da curva na região elástica
(linear).
 Tensão de escoamento (yield strength) => define a transição entre regiões elástica e
plástica => tensão que, libertada, gera uma deformação residual de 0.2 %.
 Tensão de resistência (tensile strength) => tensão máxima na curva - de engenharia.
 Ductilidade => medida da deformabilidade do material
 Resiliência => medida da capacidade de absorver e devolver energia mecânica => área
sob a região linear.
 Tenacidade (toughness) => medida da capacidade de absorver energia mecânica até a
fratura => área sob a curva até a fractura.
Resistência dos Materiais
A curva - real
 A curva  -  obtida experimentalmente é
denominada curva  - ε de engenharia.
Fractura
Esta curva passa por um máximo de tensão,
parecendo indicar que, a partir deste valor, o
material se torna mais fraco, o que não é verdade.
Isto, na verdade, é uma consequência da
estricção, que concentra o esforço numa área
menor.
Pode-se corrigir este efeito levando em conta a
diminuição de área, gerando assim a curva real.
Curva  -  real
Curva σ - ε de engenharia
Fractura
Resistência dos Materiais
Coeficiente de Poisson
•
Quando ocorre alongamento ao longo de uma direcção, ocorre contracção
no plano perpendicular.
•
A Relação entre as deformações é dada pelo coeficiente de Poisson
.
 = - y / x = - z / x o sinal de menos apenas indica que uma
extensão gera uma contracção e vice-versa.
Os valores de  para diversos metais estão entre 0.25 e 0.35.
Resistência dos Materiais
Coeficiente de Poisson
• Para uma barra sujeita a carregamento axial:

x  x  y z  0
E
• O alongamento na direcção ox é acompanhado
da contracção nas outras direcções.
Assumindo o material como isotrópico tem-se:
 y  z  0
• O coeficiente de Poisson é definido por:

y

Extensão Transversal
- - z
ExtensãoLongitudinal
x
x
Resistência dos Materiais
Exercício resolvido 2
Um cilindro de latão com diâmetro de 10 mm é traccionado ao longo do seu eixo.
Qual é a força necessária para causar uma mudança de 2.5 µm no diâmetro, no
regime elástico ?
x = d/d0 = -2.5 x10-3 /10 = -2.5 x10-4
z = - x/-2.5 x10-4 / 0.35 = 7.14 x10-4
 = E. z = 10.1 MPa x 7.14 x10-4 = 7211 Pa
F =  A0 =  d02/4 = 7211 x (10-2)2/4 = 5820 N
Resistência dos Materiais
Distorção
• Uma tensão tangencial causa uma distorção, de forma análoga a uma tracção.
 Tensão tangencial
 = F/A0 onde A0 é a área paralela à aplicação da força.
 Distorção
= tan = y/z0 onde  é o ângulo de deformação
• Módulo de distorção G
=G
Resistência dos Materiais
Distorção
• Um elemento cúbico sujeito a tensões
tangenciais deforma-se num rombóide. A
distorção correspondente é quantificada em
termos da alteração dos ângulos:
 xy  f  xy 
• Lei de Hooke: (Pequenas deformações)
 xy  G  xy  yz  G  yz  zx  G  zx
G é o módulo de distorção.
Resistência dos Materiais
Diagrama Tensão tangencial - Distorção
Com base num ensaio de torção obtêm-se os valores de tensão tangencial e respectivos valores de
distorção. Representando num gráfico os sucessivos valores obtidos no ensaio chega-se ao diagrama
Tensão tangencial - Distorção para o material em consideração.
O diagrama Tensão - Distorção é idêntico ao diagrama Tensão - Extensão obtido a partir de um ensaio
de tracção. No entanto os valores obtidos para a tensão tangencial de cedência, tensão tangencial de
rotura etc. de um dado material, são aproximadamente metade dos valores correspondentes à tracção.
 [MPa]
U
Muitos dos materiais utilizados em engenharia

têm um comportamento elástico linear e assim a  rp
Lei de Hooke para tensões tangenciais pode ser
escrita:
  G
p
p
U
r
 [rad]
Resistência dos Materiais
Relação entre E,ν, e G
G
E
2 1   
Resistência dos Materiais
Exercício resolvido 3
Um bloco rectangular de um material comum módulo de distorção G = 620 MPa é
colado a duas placas rígidas horizontais. A placa inferior é fixa, enquanto a placa
superior é submetida a uma força horizontal P. Sabendo que a placa superior se
desloca 1 mm sob acção da força, determine:
a) a distorção média no material;
b) a força P que actua na placa superior.
60 mm
200 mm
50 mm
Resistência dos Materiais
Solução
a) Distorção média no material
 xy  tan xy 
1 mm
50 mm
 xy  0.020rad
1 mm
50 mm
b) Força P actuante na placa superior
 xy  G xy
 xy  G xy  620* 0,02  12,4 MPa
P   xy A  12,4 * 200* 60  148,8 kN
Resistência dos Materiais
Carregamento Triaxial - Lei de Hooke Generalizada
• Num elemento sujeito a um carregamento multiaxial, as
componentes de extensão resultam das componentes de tensão
por aplicação do princípio da sobreposição. As condições de
aplicação do método são:
1) Cada efeito é directamente proporcional à carga que o produziu
(as tensões não excedem o limite de proporcionalidade do
material).
2) As deformações causadas por qualquer dos carregamentos é
pequena e não afecta as condições de aplicação dos outros
carregamentos.
• Tem-se:
x
x  
E
y  z  -
-
 x
E
 x
E
 y

-
E
-
 z
-
 z
y
E
 y
E

E
E
z
E