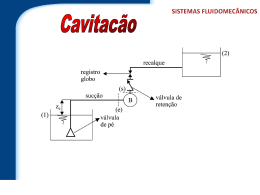
Cavitação

Matéria:







Ocorrência de cavitação em turbomáquinas com
líquidos: filme Examples of Cavitation
Efeitos da cavitação no funcionamento das
turbomáquinas
Altura de aspiração disponível
Altura de aspiração crítica
Velocidade específica de aspiração.
Coeficiente de Thoma.
Exercícios
Cavitação


Cavitação: vaporização, seguida de
condensação (quase instantânea)
Detecção da cavitação:




Alteração das curvas de funcionamento
Observação visual de formação de bolhas
Detecção de ruído e vibrações
Efeitos da cavitação:



Ruído, vibrações
Erosão do material
Redução do desempenho (rendimento, etc.)
Ocorrência de cavitação em bombas

Na situação da figura p1 é inferior à pressão atmosférica
se p1 < pvap (T)
vaporização

Contudo a pressão mínima ocorre no interior da bomba
pmin < pvap (T)
vaporização
cavitação
Ocorrência de cavitação em bombas
pmin  p1  p  pvap
para não ocorrer cavitação
Ocorrência de cavitação em bombas

Para que não ocorra cavitação:
p1  p  pvap
Hs > Hsi
p1  pvap  p
p1 V12 pvap p V12




g 2 g g g 2 g
Instalação (Hs)
po
pvap 
 p0


 es  Z asp 
g 
 g
p0 V12
p1


 es  Z asp
g g 2 g
Bomba (Hsi)
Ocorrência de cavitação em bombas

p1 V12 pvap
Altura de aspiração disponível: H s 


g 2 g g
só depende da instalação
p V12
H si 

g 2 g

Altura de aspiração crítica:
só depende da bomba

Curvas de Hsi são fornecidas pelo fabricante:
Hsi = F(Q,N,D,,, parâmetros geométricos)
Ocorrência de cavitação em bombas

Altura de aspiração
crítica (NPSH) - Hsi
(só depende da bomba)
NPSH – Net Positive
Suction Head

Curvas de H, e Hsi para o
diâmetro original (260 mm) e
após torneamento
p V12
H si 

g 2 g
Ocorrência de cavitação em turbinas

A diferença é que na definição da altura de aspiração
disponível se incluem as perdas de carga no difusor
(parte integrante do fornecimento)
Não há cavitação se
Hs > Hsi
Ocorrência de cavitação

Altura de aspiração crítica:
p V12
H si 

g 2 g
só depende da turbomáquina
Hsi = F(Q,N,D,,, parâmetros geométricos)

 Q ND 2 
H si
Aplicando a análise dimensional:  i 

 f 
,
3
H
 
 ND
Coeficiente de
Thoma crítico

Não há cavitação se:  >
Re desprezável
i
Coeficiente de Thoma  = Hs/H só depende da instalação
Ocorrência de cavitação
S

Velocidade específica de aspiração:

Velocidade específica de aspiração crítica:
Si 
N Q
gH si 3 4
 Q 
 F
3 
ND



Não há cavitação se S < Si

É indiferente utilizar Si ou i
N Q
gHs 
34
Ocorrência de cavitação

Velocidade específica de aspiração crítica:
Si 
N Q
gH si 3 4
 Q 
 F
3 
ND


i 
H si
 Q 
 f
3 
H
 ND 

Coeficiente de Thoma crítico:

Mesma família de máquinas geometricamente
semelhantes tem mesmo (Si)max e (i )max
Ocorrência de cavitação

Valores típicos:


Bombas: 2,5 < (Si)max = F() < 3,5
Turbinas: 3,5 < (Si)max = F() < 5,2
(Si)max = 3
(Si)max = 4
Ocorrência de
cavitação
Exercício 5 e 8
Qual a altura máxima a que pode colocar a bomba para que não ocorra
cavitação em cada caso? (Zasp=0,5 m; pvap=2,45 kPa; patm=101,3 kPa)
Exercícios 5 e 8 a) – Leitura directa no gráfico
1
Exercícios 5 e 8 b)
3
2
Exercícios 5 e 8 c) – leitura directa no gráfico
4
Exercícios 5 e 8 d) – leitura directa no gráfico
5