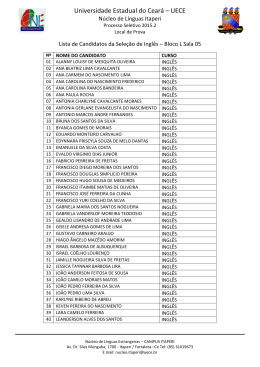
108. (UECE – 2004) Os valores de x e y que satisfazem a equação matricial
x

y

0  1
.
1   x
2  y

y   2x
4
 satisfazem, também, a relação:
6 
a) x2 + y2 = 2
b) x2 + y2 = 4
c) x2 + y2 = 8
d) x2 + y2 = 16
109. (UECE – 2005) Sejam as matrizes
 x 1
1 y 
 1 1
1 1
 , Q  
 , R  
 e S  
 .
P  
1
1
1
1
z
1






1 t 
Sobre a igualdade P.Q = R.S é possível afirmar-se corretamente:
a) nunca se verifica
b) verifica-se somente se x = y = z = t
c) verifica-se sempre que x = z = 1 e y = t
d) verifica-se quando x  z e y  t
110. (UECE – 2006) O valor de k para o qual a equação matricial X² - kX² –
1 0
1 0 
 e Y  
 , é:
k
0

k


igual a matriz identidade, sendo X  
0
a) –2
b) –1
c) 0
d) 1
1
y
111. (UNESP 2004) Considere as matrizes A  
x
1 2
4 5
, B
e C


,
z
1 1
36 45
com x, y, z números reais. Se A× B = C, a soma dos elementos da matriz A é:
a) 9.
b) 40.
c) 41.
d) 50.
e) 81.
112. (UNESP 2006) Uma fábrica produz dois tipos de peças, P1 e P2. Essas peças
são vendidas a duas empresas, E1 e E2. O lucro obtido pela fábrica com a venda de
cada peça P1 é R$ 3,00 e de cada peça P2 é R$ 2,00. A matriz abaixo fornece a
quantidade de peças P1 e P2 vendidas a cada uma das empresas E1 e E2 no mês de
novembro.
 x
 y
A matriz   , onde x e y representam os lucros, em reais, obtidos pela fábrica, no
referido mês, com a venda das peças às empresas E1 e E2, respectivamente, é:
35

20
a) 
90

48
b) 
76

69
c) 
84

 61
 28
e)  
27 
d) 
Determinantes
113. (UFMA 2006) Considere a matriz A = (aij) com i, j  {1, 2, 3,..., 180}, definida por
onde j° significa j graus.
Nessas condições, é correto afirmar que do valor do det(A) + sen
a) 1
b)
1
2

6
é:
c) -1
d) 0
e) 
3
2
x
114. Se o determinante do produto das matrizes 
1

1
1
 e 
x
x 

x
 é igual a – 1,
1 
então dois dos possíveis valores de x são números:
a) positivos
b) negativos
c) primos
d) irracionais
115. (UFMA – 2005) Considere a matriz A = (aij)3×3, definida por
e seja D =
 2 
sen
 é:
 D
3
2
1
b)
2
a)
c) 
2
2
d) 1
e) 0
1 
2 x 3

4  é nulo para um valor
116. (UECE – 2006) O determinante da matriz 1 0

 0 1 x  1
de x situado no intervalo:
a)  1, 0 
b)  0 ,1 
c)  1, 2 
d)  2 , 3 
1 2 3


117. (UECE – 2007) Considere a matriz M =  2 3 2  . A soma das raízes da
3 2 x


equação det(M²) = 25 é igual a
a) 14
b) – 14
c) 17
d) – 17
1 1
 ek
0 1
118. (UECE – 2007) Seja X = M + M² + M³ + ··· + Mk , em que M é a matriz 
é um número natural. Se o determinante da matriz X é igual a 324, então o valor de
k² + 3k – 1 é:
a) 207
b) 237
c) 269
d) 377
1  senx 
 e
1 senx 
119. (UECE – 2008) A matriz M é dada por M = P.Q, em que P = 
 cos x 0 
 . O determinante da matriz M é:
1 
 0
Q = 
a) sen(2x).
b) cos(2x).
c) sen2x.
d) cos2x.
120. (UNESP – 2002) Sejam A e B matrizes quadradas de ordem 3. Se
1 2 3


A = 0  1 1 e B é tal que B–1 = 2A, o determinante de B será:


1 0 2
a) 24.
b) 6.
c) 3.
d) 1/6.
e) 1/24.
Sistemas lineares
121. (UECE – 2007) O valor de h para que o sistema
2x  y  3z  0

x  2y - z  0
 x  hy  6 z  0

tenha a solução não nula é:
a) 5
b) 6
c) 7
d) 8
122. (UECE – 2007) Pedro recebeu a quantia de R$ 2.700,00, em cédulas de R$
10,00, de R$ 20,00 e de R$ 50,00. Sabendo que a quantidade de cédulas de R$ 20,00
é 20 vezes a de cédulas de R$ 10,00, então o número de cédulas de R$ 50,00 que
Pedro recebeu foi:
a) 15
b) 14
c) 13
d) 12
123. (UNESP – 2002) A agência Vivatur vendeu a um turista uma passagem que foi
paga, à vista, com cédulas de 10, 50 e 100 dólares, num total de 45 cédulas. O valor
da passagem foi 1 950 dólares e a quantidade de cédulas recebidas de 10 dólares foi
o dobro das de 100. O valor, em dólares, recebido em notas de 100 pela agência na
venda dessa passagem, foi:
a) 1 800.
b) 1 500.
c) 1 400.
d) 1 000.
e) 800.
124. (UNESP 2007) Uma lapiseira, três cadernos e uma caneta custam juntos, 33
reais. Duas lapiseiras, sete cadernos e duas canetas custam juntos, 76 reais. O custo
de uma lapiseira, um caderno e uma caneta, juntos, em reais, é:
a) 11.
b) 12.
c) 13.
d) 17.
e) 38.
125. (UNESP 2008) Numa campanha de preservação do meio ambiente, uma
prefeitura dá descontos na conta de água em troca de latas de alumínio e garrafas de
plástico (PET) arrecadadas. Para um quilograma de alumínio, o desconto é de R$ 2,90
na conta de água; para um quilograma de plástico, o abatimento é de R$ 0,17. Uma
família obteve R$ 16,20 de desconto na conta de água com a troca de alumínio e
garrafas plásticas. Se a quantidade (em quilogramas) de plástico que a família
entregou foi o dobro da quantidade de alumínio, a quantidade de plástico, em
quilogramas, que essa família entregou na campanha foi
a) 5.
b) 6.
c) 8.
d) 9.
e) 10.