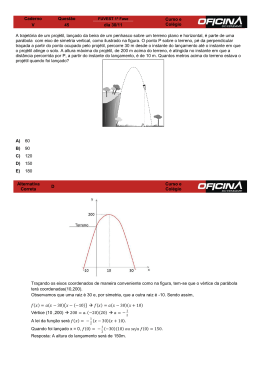
2010-2S MFA - Aula 08: Escoamento Compressíveis e Número de Mach
Breve Revisão de Termodinâmica
Número de Mach
Onda
sonora
se
propagando a partir de
c p =Rc v
uma fonte de ruído com a
cp → calor específico a pressão constante fonte estacionária.
Entalpia: h 2 −h1 =c p⋅ T 2 −T 1 
cv → calor específico a volume constante
k=
cp
cv
R=
Razão entre calores específicos.
Ru
Mm
=
constante universal dos gases
massa molar
R AR =287
[
p=⋅R⋅T
Lei dos gases ideais:
Entropia:  S =∫
]
N⋅m
kg⋅K
 
Q
T
Onda sonora se propagando a partir de
uma fonte de ruído com a fonte em
movimento. O deslocamento da fonte é
menor que a velocidade do som, assim as
ondas sonoras sempre
Fonte
se
propagarão
à
frente
da
fonte,
anunciando assim a
sua aproximação.
reversível
1a. Lei para um gás ideal com calor
específico constante:
No caso de um objeto se deslocando a uma
velocidade superior a do som (por
T
p
exemplos, os aviões caças), a região fora
 S =c p⋅ln 2 −R⋅ln 2
do cone é chamada de zona de silêncio, de
T1
p1
modo que um obejto que se aproxime a uma
velocidade supersônica não poderá ser
Processo isentrópico → caso de processo ouvido até que passe acima do observador
adiabático (Q=0) e reversível (sem perdas),
e o cone de Mach mostrado, intercepte-o.
ou seja, a variação da entropia é zero.
Para o escoamento isentrópico teremos:
T2
T1
=
 
p2
p2
k −1
k
p1
 
2
=
p 1 1
k
Fonte
2010-2S MFA - Aula 08: Escoamento Compressíveis e Número de Mach
Exemplo 01 - Argônio escoa por um
que sua condição inicial é p 1=1,7
ρ1=18 kg/m³ e sua condição final é
tubo tal Exemplo 02 - Um projétil de nariz
MPa e pontiagudo se desloca a uma velocidade de
p 2=248 M = 3 passa 200 m acima do observador.
Calcule a velocidade do projétil e determine
kPa e T2 = 400 K. Avalie (a) a temperatura a que distância do observador o projétil será
inicial, (b) a massa específica final, (c) a ouvido.
variação da entalpia e (d) a variação da
entropia do gás.