OPERAÇÕES COM CONJUNTOS
Operações com conjuntos
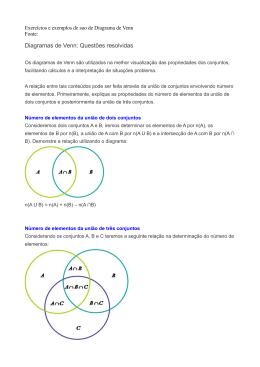
1. União de conjuntos
Dados dois conjuntos, A e B, a
união de A e B é o conjunto
formado por todos os elementos
que pertencem a A ou a B.
14243
A  B = {xx ϵ A ou x ϵ B}
A = {2, 3, 5, 7}
B = {0, 2, 4, 6}
A região hachurada
representa A  B.
A  B = {0, 2, 3, 4, 5, 6, 7}
Operações com conjuntos
2. Intersecção de conjuntos
A = {xx é um número natural menor que 8}
B = {xx é um número natural par menor que 10}
Dados dois conjuntos, A e B, a
intersecção de A e B é o conjunto
formado por todos os elementos que
pertencem a A e a B.
A região hachurada representa A  B.
A  B = {0, 2, 4, 6}
A  B = {x  x ϵ A e x ϵ B}
EXEMPLOS
1. Determinar A  B e A  B sabendo que:
A = {xx é um número natural menor que 8} e
B = {xx é um número natural entre 7 e 11}.
Resolução
Inicialmente, determinamos os elementos dos conjuntos A e B. Assim, temos:
A = {0, 1, 2, 3, 4, 5, 6, 7} e B = {8, 9, 10}
Desse modo: A  B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
AB={
}
EXEMPLOS
2. Considerar os conjuntos representados abaixo.
Resolução
a) Observe que: A = {1, 2, 3, 4}, B = {1, 2, 6, 7} e C = {1, 3, 5, 7}
Agora, determinamos (A  B): A  B = {1, 2, 3, 4, 6, 7}
Então, obtemos: (A  B)  C = {1, 3, 7}
b) Primeiro, determinamos (A  B): A  B = {1, 2}
Determinar:
a) (A  B)  C
b) (A  B)  C
Depois, determinamos a união desse conjunto com C:
(A  B)  C = {1, 2, 3, 5, 7}
EXEMPLOS
3. Sabendo que A  B = {1, 2, 3, 4, 5, 6} e A  B = {4 ,5}, escrever duas
possibilidades diferentes para A e B.
Resolução
Como A  B = {4, 5}, devemos considerar que os elementos
4 e 5 pertencem tanto ao conjunto A quanto ao conjunto B.
Sabemos também que os conjuntos A e B são formados
necessariamente pelos elementos que pertencem a A  B.
Assim, podemos escrever:
A = {1, 4, 5} e B = {2, 3, 4, 5, 6} ou
A = {3, 4, 5, 6} e B = {1, 2, 4, 5}
Há outras possibilidades além dessas.
Operações com conjuntos
3. Diferença de conjuntos
A = {xx é um número natural e está entre 20 e 30}
B = {xx é um número primo menor que 30}
A região hachurada representa A  B.
A – B = {21, 22, 24, 25, 26, 27, 28}
Dados dois conjuntos, A e B, a diferença entre
A e B é o conjunto formado pelos elementos que
pertencem a A, mas não pertencem a B.
A – B = {xx  A e x  B}
Complementar de um conjunto
OBS.: AC = complementar de A em
relação ao Universo.
Dados os conjuntos A e B, o complementar do conjunto B em relação a A é a
parte laranja da figura.
= A – B, com B  A
OBS.: Só vai existir o complementar de B em relação a A se B  A. Caso B  A,
então
= .
EXEMPLOS
1. Determinar A – B sabendo que:
A = {xx é um número natural menor que 10} e
B = {xx é um número natural e está entre 3 e 7}.
Resolução
Enumerando os elementos de A e B, temos:
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} e B = {4, 5, 6}
Como a diferença de A e B é o conjunto formado pelos
elementos que pertencem a A mas não pertencem a B, temos:
A – B = {0, 1, 2, 3, 7, 8, 9}
EXEMPLOS
2. Descrever a parte azul do diagrama por meio
de operações de conjuntos.
Resolução
Observando a figura, vemos que nenhuma parte do conjunto B está colorida, assim
como nenhuma parte do conjunto C.
Devemos observar ainda que somente uma parte do conjunto A está colorida de azul.
Como essa parte representa os elementos de A que não pertencem a B nem a C,
podemos escrever a seguinte operação para representar a parte azul da figura:
A – B – C ou A – C – B ou A – (B  C).
EXEMPLOS
3. Considerar os conjuntos A = {0, 5, 10, 15}, B = {0, 10} e
U = {xx é um número natural menor ou igual a 15}. Determinar:
a) Ac
b)
c)
, com E =
Resolução
a) Como o conjunto U é um conjunto finito, para facilitar a resolução podemos
enumerar seus elementos:
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}
Determinando U – A, encontramos:
Ac = {1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 13, 14}
Resolução
c)
b)
, com E =
b) Nesse caso, devemos determinar A – B se B  A. Assim:
= A – B = {5, 15}
c) Inicialmente, devemos encontrar os elementos do conjunto E.
Como E =
, temos: E = {5, 15}.
Agora, determinamos U – E e encontramos:
= {0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14}.
EXEMPLOS
4. Dados os conjuntos U = {3, 6, 9, 12, 15, 18},
AC = {3, 6, 9} e
BC = {15, 18}, determinar:
a) o conjunto A.
b) o conjunto B.
Resolução
a) Como AC = {3, 6, 9}, os elementos de U que não pertencem
a AC pertencem ao conjunto A; portanto:
A = {12, 15, 18}
b) Como BC = {15, 18}, os elementos de U que não pertencem
a BC pertencem ao conjunto B; portanto:
B = {3, 6, 9, 12}
Aplicação das operações com conjuntos
1. ESPORTES. Em uma pesquisa com uma turma de Ensino Médio, verificou-se
que 15 alunos praticavam basquete como atividade esportiva, 25 alunos
praticavam futebol e 7 alunos praticavam duas atividades: basquete e
futebol. Determinar quantos alunos participaram da pesquisa, sabendo
que todos optaram por pelo menos um dos dois esportes.
Resolução
Como 15 pessoas praticavam basquete e, desse total, 7 também praticavam futebol, a
quantidade de alunos que estão no conjunto A e não estão no conjunto B é: 15 – 7 = 8
n(A  B) = 8 + 18 + 7 = 33
Somente A
Somente B
2. CONSUMIDOR. Após uma pesquisa com os clientes de um supermercado,
verificou-se que 150 pessoas compraram o refrigerante da marca C e
75 compraram o da marca P. Sabendo que 200 pessoas participaram
da pesquisa, determinar quantas compraram refrigerantes das duas
marcas.
Marca C e marca P: x
Marca C: 150 – x
200 = (150 – x) + x + (75 – x)
Marca P: 75 – x
x = 150 + 75 – 200  x = 25
123
Resolução
Assim, concluímos que 25
pessoas compraram
refrigerantes das duas marcas.
3. CULTURA. Uma pesquisa foi realizada com o objetivo de identificar o tipo
de leitura preferida de 145 alunos de Ensino Médio. Nessa pesquisa,
história em quadrinhos teve 60 votos, romance, 85 votos, e ficção
científica, 55. Sabe-se ainda que 20 alunos votaram em história em
quadrinhos e em romance, 30 votaram em romance e em ficção, 10
votaram em história em quadrinhos e em ficção e 5 alunos votaram
nos três tipos. Determinar quantos alunos votaram somente em
romance. HQ (60)
Resolução
R (85)
X = 40
15
35
5
25
5
X = 85 – (15 + 5 + 25)
20
F (55)
AGORA VOCÊS FAZEM!
4. Numa pesquisa feita com 1000 famílias para verificar a audiência dos
programas de televisão, os seguintes resultados foram encontrados:
• 510 famílias assistem ao programa A,
• 305 assistem ao programa B,
• 386 assistem ao programa C,
• 180 assistem aos programas A e B,
• 60 assistem aos programas B e C,
• 25 assistem aos programas A e C, e
• 10 assistem aos três programas.
a) Quantas famílias não assistem aos três programas? 54
b) Quantas famílias assistem somente ao programa A? 315
c) Quantas famílias não assistem nem ao programa A nem ao prgrama B? 365
Resolução
n(U) = 1000
A (510)
B (305)
75
170
315
10
15
50
311
C (386)
X = 54
X = 1000 – (510 + 75 + 50 + 311) = 54
2. Certo dia um proprietário de um restaurante de cozinha italiana perguntou
a 80 dos seus clientes: “ Entre lasanha, canelone e macarronada, de qual(is)
você gosta?” O resultado da pesquisa foi o seguinte:
• 35 gostam de lasanha;
• 39 gostam de canelone;
• 40 gostam de macarronada;
• 15 gostam de lasanha e de canelone;
• 13 gostam de lasanha e macarronada;
• 11 gostam de canelone e macarronada;
• 5 gostam dos três pratos.
a) Quantos clientes gostam somente de:
Lasanha 12 - Canelone 18 - Macarronada 21
b) Quantos clientes gostam somente de lasanha ou somente de canelone ou
de ambos os pratos. 45
Resolução
n(U) = 80
L (35)
C(39)
18
10
12
5
6
8
21
M (40)
0
a)12, 18 e 21
b) 12 + 18 + 10 + 5 = 45
c) 21
5. Roberto pesquisou 34 proprietários de carros bicombustível para saber qual
combustível eles costumam utilizar em seus carros: álcool em gasolina. Dos
entrevistados, 23 utilizam álcool e 19 utilizam gasolina. Sabendo que cada
proprietário usa pelo menos um dos combustíveis,
responda as questões a
seguir.
a) Quantos proprietários utilizam os dois combustíveis?
b) Quantos proprietários utilizam somente gasolina? E apenas álcool?
Resolução
A (23)
23 – X
B (19)
X
19 – X
A (23)
15
0
23 – x + x + 19 – x = 34 → – x = 34 – 42 → x = 8
B (19)
8
11
0