Engenharia Mecânica
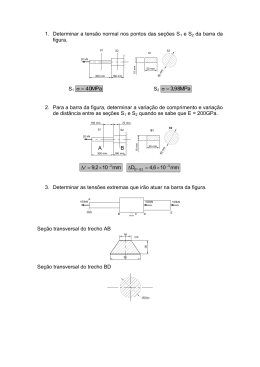
Resistência dos materiais I
LISTA 1
1. Determinar a tensão normal desenvolvida nos pontos A; B, C e D da seção
S da barra.
18cm
Ι y = 13640 cm 4
B
6cm
9,8 cm
y
y
C
2m
20cm
4m
z
A
Seção Transversal
2 tf/m
D
S
z
3tf
σ A = −431,1
6cm 6cm
kgf
kgf
kgf
σ B = −431,1 2 σ C = 0 σ D = 712,6
2
cm
cm
cm 2
2. Repetir o problema anterior quando, além dos esforços indicados, é
aplicada na extremidade esquerda da barra uma força horizontal, para a
direita, igual 20tf. Determinar, também, a posição da linha neutra.
4m
2m
2 tf/m
20tf
S
3tf
σ A = −343,4
kgf
kgf
kgf
kgf
σ D = 800,3
σ B = −343,4
σ C = 87,7
z = −2cm
2
2
2
cm 2
cm
cm
cm
3. Determinar as tensões extremas que ocorrem na barra da figura.
250 mm
20 mm
20 mm
6m
20 mm
σ=12,75MPa
Prof. José Carlos Morilla
Seção
Transversal
300 mm
5 kN/m
Engenharia Mecânica
Resistência dos materiais I
LISTA 1
4. Repetir o problema anterior quando na extremidade da direita atuar uma
força normal de tração com intensidade igual a 10 kN.
σ=13,4MPa
σ=-12,1MPa
Seção
Transversal
240mm
5. Determinar as tensões extremas da barra da figura.
20kN/m
4m
2m
máx{σ} = 83,3
200mm
min{σ} = −46,9
N
mm 2
N
mm 2
6. Determinar as tensões extremas da barra da figura.
60 mm
Seção
Transversal
2 kN
3m
90 mm
4kN/m
3m
máx{σ} = 325
N
mm 2
min{σ} = −300
N
mm 2
7. Sabendo-se que a barra da figura é construída com um material que possui
σe = 120 MPa; σe = -200MPa; σr = 300 MPa e σr = -500MPA, determinar o
máximo valor da carga P que se pode aplicar para que a barra trabalhe com
segurança 2 ao escoamento.
200 mm
250 mm
P
20 mm
3m
15 mm
P=9,7kN
Prof. José Carlos Morilla
15 mm
Seção
Transversal
Engenharia Mecânica
Resistência dos materiais I
LISTA 1
8. Repetir o problema anterior quando se aplica na extremidade livre uma
força normal de compressão de intensidade igual a 10P.
P=9,0kN
9. A barra da figura é construída com um material que possui 120MPa de
tensão admissível à tração e 150 MPa de tensão admissível à compressão.
Determinar as dimensões da seção transversal da barra quando se sabe
que h = 1,6 x b.
Seção Transversal
h
5 kN/m
3m
6m
b
b=120mm
h=192mm
10. Para a barra da figura, determinar:
a. Os módulos de resistência em relação aos eixos y e z.
b. A máxima carga P que se pode aplicar para que se possa trabalhar
com segurança 3 ao escoamento.
c. A máxima força normal de tração que junto com a carga P do item
anterior façam com que a barra trabalhe com segurança 2 ao
escoamento.
40 mm
50 mm
P
30
2m
4m
11. Deseja-se construir a estrutura da figura com barras de mesmo diâmetro.
Determinar o diâmetro destas barras quando se sabe que ela é construída
com um material que possui σ = 80MPa
Prof. José Carlos Morilla
Engenharia Mecânica
Resistência dos materiais I
LISTA 1
1,5 m
3m
2m
6 kN/m
d=95mm
12. A viga de uma pequena ponte rolante, que deve vencer um vão de 3m, foi
obtida a partir da união entre duas cantoneiras de abas iguais, como mostra
a figura que representa a seção transversal. Estas cantoneiras são
fabricadas com um aço que possui σ R = 492 MPa e σe = 352 MPa.
Determinar a capacidade de carga desta ponte rolante quando se deseja
que o coeficiente de segurança à ruptura seja igual a 5.
P
z
1,5m
203 mm
y
40
1,5m
y
Seção transversal
203 mm
y
40
y
Ι y = Ι z = 37 × 10 6 mm 4
Pmáx = 59636N
z
13. A figura representa uma prensa do tipo “C”. A estrutura desta prensa tem a
seção representada e é construída com ferro fundido que possui
σ r = 340MPa e σ r = −620MPa . Determinar para esta situação a
capacidade da prensa quando se deseja que o coeficiente de segurança
seja igual a 5 com relação a ruptura.
Prof. José Carlos Morilla
Engenharia Mecânica
Resistência dos materiais I
LISTA 1
P=237kN
14. Repetir o problema anterior considerando que a prensa é construída com
chapas de aço, soldadas entre si, que possuem σ e = 120MPa .
P=84kN
15. A barra abaixo deve ser construída com um material que possui σ R = 681
MPa, σe = 384 MPa e deve possuir uma seção transversal retangular onde
a relação entre a altura e a base é igual a 1,5. Determinar as dimensões da
seção transversal para que a barra trabalhe com segurança igual a 2,5 em
relação ao escoamento.
10kN
20kN/m
2m
2m
10kN
2m
h min = 105 mm b min = 70 mm
16. A barra abaixo deve ser construída com um material que possui σ R = 540
MPa, σe = 450 MPa e deve possuir seção circular. Determinar o diâmetro
da seção transversal para que a barra trabalhe com segurança igual a 2 em
relação ao escoamento.
Prof. José Carlos Morilla
Engenharia Mecânica
Resistência dos materiais I
LISTA 1
1kN
200 mm
2kN
300 mm
200 mm
d = 25 mm
17. Determinar o diâmetro externo da barra tubular da figura, quando se sabe
que a relação entre o diâmetro externo e o diâmetro interno é 1,5 e quando
se deseja que o coeficiente de segurança seja igual a 3 em relação ao
escoamento.
σ R = 300 MPa e σe = 120 MPa
σ R = -500 MPa e σe = -200 MPa
1m
1m
10 kN
d externo = 146 mm
Prof. José Carlos Morilla
1m
10 kN