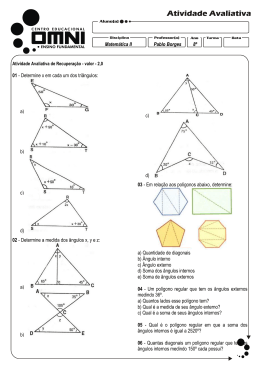
1A estrela de Davi, de seis pontas, ou selo de Salomão, também chamada de Magen
Davi, tornou-se um símbolo dos judeus no fim da Idade Média. Em tempos anteriores, ela
figurava também em símbolos cristãos e islâmicos. Foi, mais tarde, adotada pelo movimento
sionista e na bandeira de Israel. Em 1948, depois de quase 2000 anos de exílio, o Estado de
Israel foi restabelecido como o Lar Nacional Judaico. A nova bandeira foi apresentada na ONU
em 1949. A bandeira é símbolo do orgulho do retorno da Nação Judaica ao seu lar.
A
D
E
fˆ
â
b̂
ê
d̂
ĉ
B
C
F
Bandeira de Israel
As faixas horizontais e o contorno da
estrela são azuis sobre fundo branco.
Representação
Esquemática
da
Estrela de Davi, destacando-se alguns
de seus ângulos.
Dois triângulos eqüiláteros ABC e DEF idênticos entre si, são utilizados para
confeccionar a figura geométrica que representa a estrela de Davi. Nessa figura
geométrica, representada acima, foram destacados alguns ângulos. Resolva as
questões a seguir:
A)
Calcule a soma dos ângulos aˆ , bˆ , cˆ , dˆ , eˆ , fˆ indicados na figura acima.
B)
Escreva o nome do polígono formado no interior da estrela.
2O Pentágno é também o nome da sede do Departamento de Defesa dos Estados
Unidos. O Pentágono foi inaugurado no dia 15 de janeiro de 1943 e continua sendo um dos
edifícios mais famosos do mundo. Sempre foi parte das forças armadas dos Estados Unidos
desde sua construção durante a segunda guerra Mundial. Durante a primeira
metade de 1941 o departamento de guerra encontrou cada vez mais dificuldade de
fornecer um espaço para a equipe de funcionários das matrizes de seu exército em
expansão. O presidente pediu para o Congresso construir edifícios adicionais. O chefe
da construção, o brigadeiro general Brehon B. Somervell do departamento de guerra
teve uma ideia melhor, um esquema de abrigar todas as forças armadas sob um
telhado. Assim surgiu o conceito atual da sede do Pentágono.
Resolva o que se pede a seguir:
a) Calcule o valor, em graus, do ângulo interno da sede
do Pentágono nos Estados Unidos.
b) Seria possível construir diversas sedes, idênticas ao
Pentágono, encostadas no mesmo através deseus lados,
(forma de um mosaico), sem que existisse espaço ou
superposição entre elas? Justifique sua resposta por
escrito utilizando argumentos matemáticos.
3-
Fonte: brasilescola.com
A soma dos ângulos internos de um polígono regular é 2880°. Determine:
a) O número de lados do polígono.
b) A medida do ângulo interno do polígono.
c) A medida do ângulo externo do polígono.
d) O número de diagonais do polígono.
4Um polígono regular tem 20 diagonais. Determine a medida, em graus, de um de seus
ângulos internos. Um polígono regular tem 20 diagonais. Determine a medida, em graus, de um
de seus ângulos internos.
5-
O polígono regular convexo em que o número de lados é igual ao número de diagonais é o:
a) dodecágono.
c) decágono.
b) pentágono.
d) hexágono.
e) heptágono.
6Uma região de uma cidade possui o formato de um setor circular. Os pontos A, B e C
são esquinas, a distância entre os pontos A e B é de 1 km e o ângulo formado pelas ruas 1 e 2
é de 120°, conforme mostra a figura abaixo. João e Marcos desejam ir do ponto B para o ponto
C. Para tanto, João percorreu as ruas 1 e 2, passando inicialmente por A, enquanto Marcos
seguiu o trajeto da rua 3. Podemos afirmar, considerando o valor de  como 3,1 que João e
Marcos percorreram, respectivamente, uma distância aproximada de:
a)
b)
c)
d)
e)
2 km e 2,09 km
2 km e 2 km
1 km e 2 km
2,09 km e 2,09 km
2 km e 1 km
7“Os primeiros Jogos Olímpicos da Era Moderna, em 1896, já incluíam o ciclismo em seu
programa oficial - com uma prova de 87 km entre Atenas e Marathon. Os Jogos PanAmericanos também incluem o esporte desde sua primeira edição, em Buenos Aires-1951.”
(fonte: Globo Esporte)
Um ciclista percorre uma pista circular de 15 metros de raio, para cumprir esta prova
de 87 km. Considerando   3,14 , o número aproximado de voltas a serem dadas por
esse ciclista é equivalente a;
a)
b)
c)
d)
675.
923.
1.087.
776.
8a)
b)
c)
d)
e)
O nome do polígono, cuja soma dos ângulos internos é 2340°, é:
decágono.
dodecágono.
undecágono.
pentadecágono.
icoságono.
9O apótema do quadrado inscrito numa circunferência é igual a 2 cm. Determine a área do
hexágono regular inscrito nessa mesma circunferência.
10Um triângulo equilátero e hexágono regular está inscritos em uma mesma circunferência. Se o
lado do triângulo equilátero mede 12cm, determine o apótema do hexágono regular.
a  5 2cm e os ângulos indicados valem A = 30º e B = 45º. Calcule b.
11-
. No triângulo,
12-
Na figura mostrada, determine:
a) o cosseno do ângulo α.
b) a medida do segmento AD.
13-
a)20
O perímetro de o triângulo a seguir é:
b)30 c) 40
d)36 e)18
14- (UNICAMP) – A água utilizada na casa de um sítio é captada e bombeada do
rio para uma caixa-d’água a 50m de distância. A casa está a 80m de distância da
caixa-d’água e o ângulo formado pelas direções caixa-d’água-bomba e caixad’água-casa é de 60º. Se se pretende bombear água do mesmo ponto de captação
até a casa, quantos metros de encanamento são necessários?
15- Os irmãos André, Paulo e Vitor moram em casas localizadas na mesma fazenda. Sabe-se que a
casa de André dista 500 m da casa de Paulo e 800 m da casa de Vitor, e que o ângulo formado entre
essas direções é 60°. Pode-se concluir que a distância entre a casa de Paulo e a casa de Vitor é de: