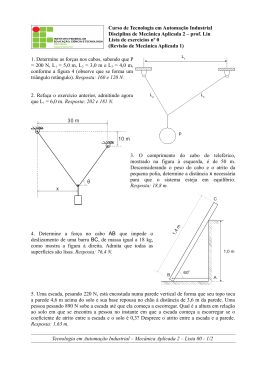
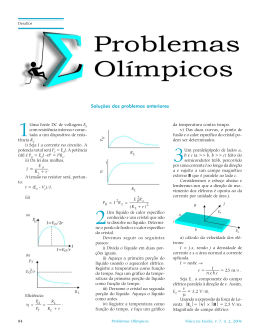
PROJETO CIÊNCIA NA BAGAGEM
Roteiro para estudo de vídeo
Prof.:
Patrocínio:
FINEP
Curso:
Data: _____/_____/_____
Aluno:
Sala :
n°:
Turma:
Aluno:
n°:
Roteiro elaborado por Luiz André Mützenberg para o filme vt_cb_20.mpg - Projeto Ciência na Bagagem - http://gaia.liberato.com.br/ciencianabagagem
CILINDRO DESOBEDIENTE
Objetivo: estudar as condições necessárias para que um cilindro comece a rolar em um plano inclinado.
O cilindro permanece em equilíbrio no plano inclinado quando ele satisfaz a condição de equilíbrio de translação também chamada de equilíbrio da partícula,
n 
Eq. 1
 Fi  0 ,
i 1
e a condição de equilíbrio de rotação, também conhecida
como equilíbrio do corpo rígido:
n

Eq. 2
 i  0
i 1
Entre o cilindro e o plano inclinado ocorre atrito estático, assim, o valor da força de atrito anula a componente
da força peso, paralela ao plano inclinado, para que seja
satisfeita a primeira condição de equilíbrio. A condição de
equilíbrio de translação deve ser analisada quando o coeficiente de atrito for muito pequeno ou quando o centro de
massa do cilindro estiver muito afastado do eixo. Estas
situações não ocorrem nas experiências folmadas.
1. O que poderia acontecer com o cilindro se não existisse
atrito com o plano inclinado? Explique.
m1
R
d
m2
•
CM
R2
C
r

•eixo

Para que o cilindro permaneça em equilíbrio, o centro de
massa (CM) deve estar à esquerda da linha vertical que passa
pelo ponto de contato entre o cilindro e o plano inclinado (eixo). Para analisar se esta condição é satisfeita você deve seguir
os passos a seguir.
2. Mostre que os ângulos  e  são iguais.
3. Mostre que:
d .m2
Eq. 3
r
m1 .m2
4. Como pode calcular a inclinação limite, isto é na maior inclinação em que ainda é possível manter o cilindro em equilíbrio
sobre o plano inclinado. Explique.
a)
b)
Fig. 2. – Inclinação necessária para que o cilindro comece a se mover: a) quando o centro de massa coincide com o eixo; e b) quando o
centro de massa não coincide com o eixo.
5. O que acontece com a inclinação limite quando a distância d
entre os centros de massa da casca cilíndrica e do cilindro aumenta? Justifique a resposta.
6. A distância d pode ser igual ao raio R da casca esférica?
Explique.
A casca cilíndrica que aparece no vídeo “cilindro desobediente” possui raio R=100 mm e massa m1=775 g. O cilindro
fixado no interior da casca cilíndrica possui massa m2=197 g.
7. Determine a inclinação limite. Tome como base a Fig 2b.
8. Use o resultado do item anterior para determinar a distância r
entre o eixo da casca cilíndrica e o centro de massa do sistema.
9. Qual é a distância entre os centros de massa da casca cilíndrica e do cilindro que aparecem no vídeo.
10. É possível construir um sistema, idêntico ao representado
na Fig. 1, capaz de permanecer em equilíbrio em planos inclinados com ângulo maior que 45°? Justifique a resposta.
Fig. 1. – Condição limite, o cilindro está prestes a rolar.
Conclusão: ___________________________________________________________________________________________