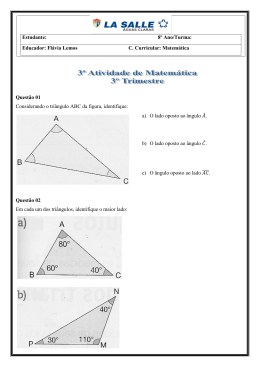
 RESUMO TEÓRICO 
a 2  b 2  c 2  2  b  c  cos 
a
ˆ
sen A

b
c

 2R
ˆ sen C
ˆ
sen B
Ângulos Notáveis

30o
45o
60o
120o
135o
150o
sen 
1
2
3
2
3
2
1
2
3
2
1

2
2
2
2

2
1
2
cos 
2
2
2
2

3
2
1
 ATIVIDADES 
 PARTE A 
1) Calcule a medida do lado BC a seguir:
2) Um paralelogramo tem lados 4cm e 6 cm e um dos ângulos internos medindo 60o .
a) Desenhe o paralelogramo indicando todas as medidas dos lados e dos ângulos internos.
b) Calcule a medida da diagonal menor.
c) Calcule a medida da diagonal maior.
3) (CFTRJ - 2014) Considerando que ABC é um triângulo tal que AC  4 cm, BC  13 cm e   60,
calcule os possíveis valores para a medida do lado AB.
4) Considere um triângulo de lados medindo 4cm, 5cm e 6cm.
a) Calcule a medida do cosseno do ângulo formado pelos lados de medidas 4cm e 6cm.
b) Calcule a medida da mediana relativa ao lado maior.
 PARTE B 
5) Na figura abaixo, os ângulos do triângulo medem a  = 60o e Ĉ = 45o e o lado AB mede 2 cm.
Determine a medida: a) do lado CB
b) do raio da circunferência.
A
B
C
6) No triângulo da figura o ângulo  mede 60o, o ângulo Ê mede 45o e o lado EO mede 4 3 cm.
Calcule: a) A medida do lado AO
b) a medida do raio da circunferência.
2
7) (UFSM 2005) Na instalação das lâmpadas de uma praça de alimentação, a equipe necessitou
calcular corretamente a distância entre duas delas, colocadas nos vértices B e C do triângulo, segundo
a figura. Assim, a distância "d" é
a) 50 2 m
b) 50
( 6)
m
3
c) 50 3 m
d) 25 6 m
e) 50 6 m
 PARTE C 
8) Sabendo que num paralelogramo um dos ângulos mede 60o e que os lados medem 5 cm e 8 cm,
podemos dizer que a diagonal menor mede:
a) 3 3 cm
b) 4 3 cm
c) 6 3 cm
d) 6,4 cm
9) Em um triângulo ABC, os lados AB e AC medem respectivamente 2 cm e
e) 7 cm
3 cm e formam um
ângulo de 30o. Calcule a medida do lado BC .
a) 1 cm
b)
2 cm
c) 2 cm
d) 3 cm
e) 5 cm
10) (UFSM 2013) A caminhada é uma das atividades físicas que, quando realizada com frequência,
torna-se eficaz na prevenção de doenças crônicas e na melhora da qualidade de vida.
Para a prática de uma caminhada, uma pessoa sai do ponto A, passa pelos pontos B e C e retorna ao
ponto A, conforme trajeto indicado na figura.
Quantos quilômetros ela terá caminhado, se percorrer todo o trajeto?
a) 2,29.
b) 2,33.
c) 3,16.
d) 3,50.
e) 4,80.
11) (UFRGS 2013) Os lados de um losango medem 4 e um dos seus ângulos 30°. A medida da
diagonal menor do losango é
a) 2 2  3 .
b)
2  3.
c) 4 2  3 .
d) 2 2  3 .
e) 4 2  3 .
12) (G1 - IFSP 2014) A base de um triângulo isósceles mede 3 3 cm e o ângulo oposto à base mede
120°. A medida dos lados congruentes desse triângulo, em centímetros, é
a) 3.
b) 2.
c) 3.
d) 1  3.
e) 2  3.
3
13) (UFPR 2014) Dois navios deixam um porto ao mesmo tempo. O primeiro viaja a uma velocidade de
16 km/h em um curso de 45° em relação ao norte, no sentido horário. O segundo viaja a uma
velocidade 6 km/h em um curso de 105° em relação ao norte, também no sentido horário. Após uma
hora de viagem, a que distância se encontrarão separados os navios, supondo que eles tenham
mantido o mesmo curso e velocidade desde que deixaram o porto?
a) 10 km.
b) 14 km.
c) 15 km.
d) 17 km.
e) 22 km.
14) (UNESP 2013) Um professor de geografia forneceu a seus alunos um mapa do estado de São
Paulo, que informava que as distâncias aproximadas em linha reta entre os pontos que representam as
cidades de São Paulo e Campinas e entre os pontos que representam as cidades de São Paulo e
Guaratinguetá eram, respectivamente, 80km e 160km. Um dos alunos observou, então, que as
distâncias em linha reta entre os pontos que representam as cidades de São Paulo, Campinas e
Sorocaba formavam um triângulo equilátero. Já um outro aluno notou que as distâncias em linha reta
entre os pontos que representam as cidades de São Paulo, Guaratinguetá e Campinas formavam um
triângulo retângulo, conforme mostra o mapa.
Com essas informações, os alunos determinaram que a distância em linha reta entre os pontos que
representam as cidades de Guaratinguetá e Sorocaba, em km, é próxima de
a) 80  2  5  3
b) 80  5  2  3
c) 80  6
d) 80  5  3  2
e) 80  7  3
15) (UNICAMP2013) Na figura abaixo, ABC e BDE são triângulos isósceles semelhantes de bases 2a e
ˆ  30. Portanto, o comprimento do segmento CE é:
a, respectivamente, e o ângulo CAB
a) a
5
3
b) a
8
3
c) a
7
3
d) a 2
4
16) (UNESP 2012) No dia 11 de março de 2011, o Japão foi sacudido por terremoto com intensidade
de 8,9 na Escala Richter, com o epicentro no Oceano Pacífico, a 360 km de Tóquio, seguido de
tsunami. A cidade de Sendai, a 320 km a nordeste de Tóquio, foi atingida pela primeira onda do tsunami
após 13 minutos. (O Estado de S.Paulo, 13.03.2011. Adaptado.)
Baseando-se nos dados fornecidos e sabendo que cos   0,934 , onde  é o ângulo Epicentro-TóquioSendai, e que 28  32  93,4  215 100 , a velocidade média, em km/h, com que a 1ª onda do tsunami
atingiu até a cidade de Sendai foi de:
a) 10.
b) 50.
c) 100.
d) 250.
e) 600.
17) (PUCRJ 2012) Seja um hexágono regular ABCDEF. A razão entre os comprimentos dos segmentos
AC e AB é igual a:
a)
2
b)
3
2
c)
1 5
2
d)
3
e) 2
18) (UFTM 2012) Na figura estão posicionadas as cidades vizinhas A, B e C, que são ligadas por
estradas em linha reta. Sabe-se que, seguindo por essas estradas, a distância entre A e C é de 24 km,
e entre A e B é de 36 km.
Nesse caso, pode-se concluir que a distância, em km, entre B e C é igual a
a) 8 17.
b) 12 19.
c) 12 23.
d) 20 15.
e) 20 13.
19) (G1 - IFAL 2011) Num paralelogramo, cada ângulo agudo mede 30° e os lados que formam cada
um desses ângulos medem 3 3 cm e 5 cm. Calcule a medida da menor das diagonais desse
paralelogramo.
a) 6 cm
b) 3 cm
c) 3 3 cm
d) 7 cm
e) 15 3 cm
5
20) (G1 - CFTCE 2007) Na figura a seguir, determine o valor de x e o perímetro do triângulo.
21) (UFSCAR 2006) Se os lados de um triângulo medem x, x + 1 e x + 2, então, para qualquer x real e
maior que 1, o cosseno do maior ângulo interno desse triângulo é igual a
a) x / (x + 1).
b) x / (x + 2).
c) (x + 1) / (x + 2).
d) (x - 2) / 3x.
e) (x - 3) / 2x.
22) (Ufrgs 2004) Na figura a seguir, os ângulos u e v medem, respectivamente,
OQ =
π
2π
e
, OP =
4
3
2e
3.
Então, (PQ)2 é
a) 2 + 3 .
b) 3 + 2 .
c) 2 + 2 .
d) 3 + 3 .
e) ( 2 ) +
3.
23) (UFPI 2000) Em um triângulo, um dos ângulos mede 60° e os lados adjacentes a este ângulo
medem 1cm e 2cm. O valor do perímetro deste triângulo, em centímetros, é:
a) 3 + 5
b) 5 + 3
c) 3 + 3
d) 3 + 7
e) 5 + 7
 PARTE D 
24) Dado o triângulo a seguir:
O valor de x é:
a) 4 2
b)
3
c) 2 3
d) 4 6
e) 6 6
6
25) Uma circunferência é circunscrita ao triângulo ABC. Sabendo que o lado AC mede 4cm e que o
ângulo oposto a AC mede 30o a medida do raio da circunferência é:
a) 4 cm
b) 4 3 cm
c) 4 2 cm
d) 2 cm
e) 1 cm
26) (UFJF 2012) Uma praça circular de raio R foi construída a partir da planta a seguir:
Os segmentos AB, BC e CA simbolizam ciclovias construídas no interior da praça, sendo que
AB  80 m. De acordo com a planta e as informações dadas, é CORRETO afirmar que a medida de R é
igual a:
a)
160 3
m
3
b)
80 3
m
3
c)
16 3
m
3
d)
8 3
m
3
e)
3
m
3
27) (UFSM 2011) A figura a seguir apresenta o delta do rio Jacuí, situado na região metropolitana de
Porto Alegre. Nele se encontra o parque estadual Delta do Jacuí, importante parque de preservação
ambiental. Sua proximidade com a região metropolitana torna-o suscetível aos impactos ambientais
causados pela atividade humana.
A distância do ponto B ao ponto C é de 8 km, o ângulo A mede 45° e o ângulo C mede 75°. Uma
maneira de estimar quanto do Delta do Jacuí está sob influência do meio urbano é dada pela distância
do ponto A ao ponto C. Essa distância, em km, é
a)
8 6
3
b) 4 6
c) 8 2  3
d) 8( 2  3 )
e)
2 6
3
28) (UFPB 2010) A prefeitura de certa cidade vai construir, sobre um rio que corta essa cidade, uma
ponte que deve ser reta e ligar dois pontos, A e B, localizados nas margens opostas do rio. Para medir a
distância entre esses pontos, um topógrafo localizou um terceiro ponto, C, distante 200m do ponto A e
7
na mesma margem do rio onde se encontra o ponto A. Usando um teodolito (instrumento de precisão
para medir ângulos horizontais e ângulos verticais, muito empregado em trabalhos topográficos), o
topógrafo observou que os ângulos B Ĉ A e C Â B mediam, respectivamente, 30º e 105º, conforme
ilustrado na figura a seguir.
Com base nessas informações, é correto afirmar que a distância, em metros, do ponto A ao ponto
B é de:
a) 200 2
b) 180 2
c) 150 2
d) 100 2
e) 50 2
29) (UFG 2012) Observe a figura a seguir, em que estão indicadas as medidas dos lados do triângulo
maior e alguns dos ângulos.
O seno do ângulo indicado por α na figura vale:
a)
4 3 3
10
b)
4 3
10
c)
43 3
10
d)
43 3
10
e)
4 3 3
10
30) (UFPE 2004) Uma ponte deve ser construída sobre um rio, unindo os pontos A e B, como ilustrado
na figura a seguir. Para calcular o comprimento AB, escolhe-se um ponto C, na mesma margem em
que B está, e medem-se os ângulos CBA = 57° e ACB = 59°. Sabendo que BC mede 30m, indique, em
metros, a distância AB. (Dado: use as aproximações sen(59°) ≈ 0,87 e sen(64°) ≈ 0,90)
8
31) (UNESP 2003) Cinco cidades, A, B, C, D e E, são interligadas por rodovias, conforme mostra a
figura.
A rodovia AC tem 40 km, a rodovia AB tem 50 km, os ângulos x, entre AC e AB, e y, entre AB e BC, são
3
3
tais que senx =
e seny = . Deseja-se construir uma nova rodovia ligando as cidades D e E que,
4
7
dada a disposição destas cidades, será paralela a BC.
a) Use a lei dos senos para determinar quantos quilômetros tem a rodovia BC.
b) Sabendo que AD tem 30 km, determine quantos quilômetros terá a rodovia DE.
32) (UNESP 1997) Para calcular a distância entre duas árvores situadas nas margens opostas de um
rio, nos pontos A e B, um observador que se encontra junto a A afasta-se 20m da margem, na direção
da reta AB, até o ponto C e depois caminha em linha reta até o ponto D, a 40m de C, do qual ainda
pode ver as árvores.
Tendo verificado que os ângulos DCB e BDC medem, respectivamente, cerca de 15° e 120°, que valor
ele encontrou para a distância entre as árvores, se usou a aproximação
6 = 2,4?
33) (CESGRANRIO 1994) No triângulo ABC, os lados AC e BC medem 8 cm e 6 cm, respectivamente,
e o ângulo A vale 30°. O seno do ângulo B vale:
a) 1/2
b) 2/3
c) 3/4
d) 4/5
e) 5/6
34) (UNICAMP 1999) Sejam A, B e C pontos de uma circunferência tais que, AB =2km, BC =1km e a
 C seja de 135°.
medida do ângulo A B
a) Calcule o raio dessa circunferência.
b) Calcule a área do triângulo ABC.
9
 RESPOSTAS / SOLUÇÕES 
 PARTE C 
8) Alternativa: e) 7 cm
9) Alternativa: a) 1 cm
10) Alternativa: D
Solução: Pela Lei dos Cossenos, obtemos:
2
2
2
BC  AC  AB  2  AC  AB  cosBAC
 (0,8)2  12  2  0,8  1 cos150

3

 0,64  1  2  0,8   
 2 
 1,64  0,8  1,7
 3.
Logo, BC  1,7 e, portanto, o resultado é 1  0,8  1,7  3,5.
11) Alternativa: C
Solução: Considere a figura.
Como AB  AD  4 u.c. e BAD  30, pela Lei dos Cossenos, obtemos
2
2
2
BD  AB  AD  2  AB  AD  cosBAD
 42  42  2  4  4 
3
2
 2  16  16 3.
Portanto, BD  4 2  3 u.c.
12) Alternativa: A
Solução:
Aplicando o teorema dos cossenos, temos:
10
3 3 
2
 x 2  x 2  2  x  x  cos120
 1
27  2x 2  2x 2    
 2
27  3x 2
x2  9
x  3
Logo, a medida dos lados congruentes desse triângulo, em centímetros, é 3 cm.
13) Alternativa: B
Solução: Depois de uma hora de viagem o navio 1 (N1) terá percorrido 16 km e o navio 2 (N2) terá
percorrido 6 km. Temos, então, a seguinte figura:
Sendo d a distância entre os navios, temos:
d2  162  62  2  16  6  cos60
 1
d2  256  36  192   
2
d2  196
d  14km
14) Alternativa: B
Solução: Sejam S, P, G e C, respectivamente, os pontos que representam as cidades de Sorocaba,
São Paulo, Guaratinguetá e Campinas.
  60 e CPG
  150. Logo, aplicando a Lei dos Cossenos no triângulo
  90, vem SPG
Sabendo que SPC
SPG, encontramos
2
2
2

SG  SP  PG  2  SP  PG  cosSPG
 802  1602  2  80  160  cos150

3

 6400  25600  2  12800   
 2 


 6400  (5  2  3 )
Portanto, SG  80  5  2  3 km.
11
15) Alternativa: C
Solução:
No ΔCMB : cos30° 
a
3 a
2a

 x
x
2
x
3
a
3
a
a
No ΔENB : cos30°  2 

y
y
2
2y
3
ˆ  180  30  30  120
CBE
Aplicando o teorema dos cossenos no triângulo CBE, temos:
CE2  x 2  y 2  2.x.y.cos120
CE2 
4a2 a2
2a a  1 

 2

 
3
3
3
3  2
CE2 
5a2 2a2

3
3
CE2 
7a2
3
CE  a.
7
3
16) Alternativa: E
Solução: Considere a figura.
Sabendo que ET  360km, ST  320km, cos   0,934 e que 28  32  93,4  215100, pela Lei dos
Cossenos, vem
2
2
2
ES  ET  ST  2  ET  ST  cos  
2
ES  3602  3202  2  360  320  0,934 
2
ES  129600  102400  2  22  32  25  93,4 
2
ES  232000  28  32  93,4 
2
ES  232000  215100 
ES  16900  ES  130km.
12
Portanto, como 13min 
130
13
 600km h.
h, temos que a velocidade média pedida é dada por
13
60
60
17) Alternativa: D
Solução:
AC2  a2  a2  2  a  a  cos120  AC  a 3
Logo,
AC a 3

 3.
AB
a
18) Alternativa: B
Solução:
Aplicando a Lei dos Cossenos, obtemos
2
2
2
BC  AB  AC  2  AB  AC  cosBAC 
2
 1
BC  362  242  2  36  24     
 2
2
BC  1296  576  864 
BC  2736  12 19 km.
19) Alternativa: D
Solução: Aplicando o teorema dos cossenos, temos:
d2 = 52 + ( 3 3 )2 – 2.5. 3 3 .cos30o
d2 = 25 + 27 -30 3.
3
2
d2 = 52 – 45
d=
20) Resposta: x =
21) Alternativa: E
7
3
e o perímetro vale 2P = 7,5 cm
2
22) Alternativa: A
23) Alternativa: C
13
 PARTE D 
24) Alternativa: E
25) Alternativa: A
26) Alternativa: B
Solução: Pela Lei dos Senos, segue que:
AB
80
80 3 80 3
 2R  2R 
R


m.
sen60
3
3
3 3
2
27) Alternativa: B
Solução:
α= 180o  75o  45o  60o
Aplicando o teorema dos senos, temos:
AC
sen60
o

8
sen45o
2
3
 8.
2
2
AC  4 6
AC.
28) Alternativa: D
Solução:
x
sen30o
x
x

200
sen45o
2
1
 200 
2
2
200
2
x  100 2m
14
29) Alternativa: A
Solução: Considere a figura, na qual AB  6, AC  10 e BC  8.
Do triângulo retângulo ABD, obtemos
tgBAD 
BD
AB
 BD  AB  tg30
3
3
 BD  6 
 BD  2 3.
Além disso, pelo Teorema do Ângulo Externo, segue que

ADC  DAB  ABD
 30  90
 120.
Portanto, pela Lei dos Senos, vem
CD
senDAC
30) Resposta: 29 metros.

AC

sen ADC
82 3
10

sen 
sen120
 sen  
4 3
 sen60
5
 sen  
4 3 3

5
2
 sen  
4 3 3
.
10
31) Respostas:
a) BC = 70 km
b) DE = 42 km
32) Resposta: A distância entre as duas árvores é de 28 metros.
33) Alternativa: B
34) Respostas:
a) R =
52 2
km
2
b) S =
2
km2
2
15