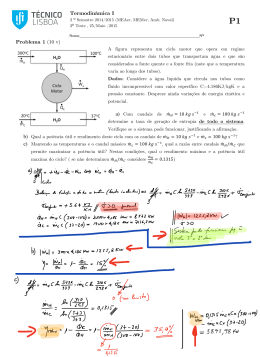
P1
Termodinâmica I
Ano Lectivo 2007/08
1º Ciclo-2ºAno/2º semestre (LEAmb LEAN MEAer MEMec)
2º Exame , 11/Julho /2008
Nome:
Nº
Sala
Problema 1 (2v+2v+1v)
900
300
T (K)
T (K)
Considere um sistema fechado constituído por um êmbolo e com ar no seu interior (modelado como gás perfeito com Cp =1 kJ/kg
K) e que pode executar dois ciclos reversíveis representados nos seguintes diagramas T-s:
b
c
a
200
d
400 S (kJ/kg K)
B
900
300
A
200
C
300
400 S (kJ/kg K)
a) Calcule o trabalho específico produzido por cada ciclo?
b) Indique nos dois diagramas T-s os percursos ao longo do quais é recebido calor . Calcule o calor específico recebido e o
trabalho específico associado a esses troços, para cada ciclo.
c) Qual é o rendimento termodinâmico de cada ciclo? Compare com o máximo rendimento termodinâmico para este tipo de
ciclos reversíveis e comente.
NOTA: A massa molar do ar é 28.97 kg/kmol.
R = 8,314kJ/kmol.K
P2
Termodinâmica I
Ano Lectivo 2007/08
1º Ciclo-2ºAno/2º semestre (LEAmb LEAN MEAer MEMec)
2º Exame , 11/Julho /2008
Nome:
Nº
Sala
Problema 2 (2v+2v+1v)
Considere um ciclo de Rankine ideal com sobreaquecimento constítuido por um gerador de vapor, uma turbina, um condensador e
uma bomba. A pressão no condensador e no gerador de vapor é respectivamente igual a 0.08 bar e 80 bar. À saída do condensador
(secção 3) a água está na fase de liquido saturado e à saída do gerador de vapor a temperatura é T1 = 600º C .
a) Represente o ciclo no diagrama T-s, calcule a entalpia nas quatro secções e a eficiência térmica do ciclo
b) Para melhorar a eficiência térmica sugeriu-se a utilização no gerador de vapor de uma pressão igual a 240 bar. Mantendo
c)
inalterados os restantes dados ( T1 = 600º C , pressão no condensador igual a 0.08 bar, 3 liquido saturado), represente o
novo ciclo no diagrama T-s, calcule a entalpia nas quatro secções e a nova eficiência térmica.
Utilizando o método das áreas mostre que a diminuição de entalpia na saída do gerador de vapor (secção 1) da alínea a)
para a alínea b) implica que β T > 1 , sendo β o coeficiente de dilatação a pressão constante.
1
Saída
vapor
Ciclo a)
h (kJ/kg)
Ciclo b)
h (kJ/kg)
2
gerador Saída da turbina
3
Saída condensador
4
Saída da bomba
Termodinâmica I
P3
Ano Lectivo 2007/08
1º Ciclo-2ºAno/2º semestre (LEAmb LEAN MEAer MEMec)
2º Exame , 11/Julho /2008
Nome:
Nº
Sala
Problema 3 (2v+0.5v+0.5v+1v+1v)
O aquecimento da água de uma piscina é feito com recurso a uma bomba de calor. A bomba de calor usa refrigerante 22 como
fluido frigorífico e extrai energia da água do subsolo que está a 8ºC. O compressor é accionado por um motor eléctrico com um
rendimento de quase 100%. A piscina pode ser considerada como adiabática e os 150m3 de água da piscina estão inicialmente a
10ºC. O objectivo é aquecer a água da piscina até aos 18ºC.
O refrigerante, com um caudal de 1 Kg/s, entra no compressor como vapor saturado a 0ºC (estado 1) e sai a 1MPa e 60ºC (estado
2). O refrigerante sai do condensador líquido saturado (estado3).
a) Complete a tabela 1.
b) Qual o rendimento isentropico do compressor?
c) Qual a eficiência do ciclo?
d) Durante quanto tempo deve a bomba de calor funcionar para a água da piscina passar dos 10 ºC para os 18ºC?
e) Se o aquecimento da água fosse feito através de resistências eléctricas, quanto mais energia eléctrica era necessário gastar,
comparada com o uso da bomba de calor? Justifique.
Nota: Calor especifico da água 4.18 KJ/kg K, massa especifica da água 1000kg/m3
a)
Estado
1- Entrada
compressor
2-saida compressor
real
2i- saída do
compressor ideal
3- saida condensador
4- entrada
evaporador
T
(ºC)
0
60
P(Pa)
106
s (KJ/kg K)
h (KJ/Kg)
Solução
a)
Estado
1- Entrada
compressor
2- saída
compressor
2i- saida
compressor ideal
3- saída
condensador
4- Entrada
Evaporador
T (ºC)
0
P(Pa)
s (KJ/kg K)
4.98x105 0.9271
h (KJ/Kg)
249.92
106
0.9902
287.15
Xxxxx
106
xxxxx
23.49 106
0.9271
267.22
0.2748
73.30
4.98x105 0.2823
73.30
60
0
H4=h3=73.30=x4 hg-(1-x4)hf
x4= (73.30-45.12)/204.81=0.14
S4=0.14*0.9271+(1-0.14)*0.1773=0.2823 kj/kg K
b)s2i=s1= 0.9271 kj/kg K h2i=267.22kJ/kg
rendiemnto isentropico compressor= (267.22-249.92)/(287.15-249.92)= 0.46
c) e=(h2-h3)/(h2-h1)=(287.15-73.30)/(287.15-249.92)=5.75
d) Calor necessário para aquecer a água = m C (Tf-Ti) =
150000 *4.18 * (18-10)=5016000 kJ
t= 5016000/(m*(h2-h3))= 5016000(1*(287.15-73.30))/3600=6.5horas
e)5016000/(1*(287.15-249.92)*6.5*3600)=5.75
valor igual à eficiência do ciclo, a energia obtida é igual a 5.75 vezes a energia gasta
no compressor.
P4
Termodinâmica I
Ano Lectivo 2007/08
1º Ciclo-2ºAno/2º semestre (LEAmb LEAN MEAer MEMec)
2º Exame , 11/Julho /2008
Nome:
Nº
Sala
Problema 4 (1v+2v+2v)
Patm = 1 bar
Tamb = 300K
10 kg Água
x=0,3
Êmbolo B
Êmbolo A
5 kg Ar
320 kg Ar
P = 0,5 bar
Considere o seguinte sistema termodinâmico em equilíbrio. O cilindro A
permite trocas de calor e está ligado ao cilindro B por um tubo onde existe
uma válvula. Este tubo tem um volume desprezável e é adiabático.
Inicialmente o êmbolo A está fixo e a válvula está fechada. No cilindro B
existe um êmbolo móvel que separa água de ar. As paredes exteriores do
cilindro B também permitem trocas de calor. Os êmbolos têm massas
desprezáveis e o atrito entre os êmbolos e as paredes dos respectivos
cilindros é desprezável. O sistema está inicialmente em equilíbrio.
a)
Caracterize o estado de equilíbrio inicial dando o valor da
temperatura do ar em A, a temperatura e a pressão do ar em B e a
temperatura e a pressão da água.
b) Suponha que o êmbolo A é solto e a válvula é aberta. Qual o novo estado de equilíbrio do sistema (indique valores de
pressão e temperatura para o ar em A, o ar em B e a água). Justifique. Represente qualitativamente o estado inicial e o
estado final do ar no cilindro A, do ar no cilindro B e da água no cilindro B em diagramas temperatura – volume específico.
c) Qual a quantidade de energia transferida sob a forma de calor entre o compartimento A e o exterior?
NOTA: A massa molar do ar é 28.97 kg/kmol.
R = 8, 314kJ/kmol.K
a) Ar em A
Ti = 300K (equilíbrio com a atmosfera)
Água em B
Ti = 300K (equilíbrio com a atmosfera)
Pi = Psat(300K)=0.03567 bar
Ar em B
Ti = 300K (equilíbrio com a atmosfera)
Pi = 0.03567 bar (equilíbrio com a água)
b) Ar em A
Tf = 300K (equilíbrio com a atmosfera)
Pf = 1 bar (equilíbrio com a atmosfera)
Vi =miRTi/Pi=551m3
vi = 1.72 m3/kg
Ar em B
Tf = 300K (equilíbrio com a atmosfera)
Pf = 1 bar (equilíbrio com o ar em A)
Vi = miRTi/Pi=120.68m3
vi = 24.14 m3/kg
Água em B
Tf =300K (equilíbrio com a atmosfera)
Pf =1 bar (equilíbrio com o ar em B)
Àgua está no estado de liquido comprimido
Vi =mi(xvg+(1-x)vf)=116 m3
vi = 11.6 m3/kg
Vf = mivf = 0.01 m3
vf = 0.001 m3/kg
VB= Vi (ar em B) + Vi (água em B) = 237.01 m3
Ar em B
Vf = VB – Vf(água em B) = 237 m3
mf = PfVf / (RTf )=275.28kg
vf = 0.86 m3/kg
mar total = mi (ar em B) + mi (ar em A) = 325 kg
Ar em A
mf = mar total – mf (B) = 49.72 kg
Vf =mfRTf/Pf = 42.81 m3
vf = 0.86 m3/kg
NOTA: A representação nos diagramas T-v é qualitativa e portanto não era
calcular os volumes específicos
Vf
W = − ∫ PdV = − Patm (V f − Vi ) = 50821kJ
Vi
c)
∆U = u (300) ( m f − mi ) = −57858kJ
∆U = W + Q + ( m f − mi ) hout ⇒
Q = −27544kJ
necessário