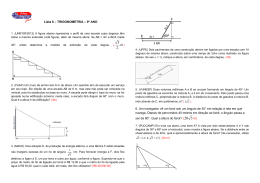
3º
EM
LISTA 04
Fabio Henrique
1) Um topógrafo foi chamado para obter a altura de um edifício. Para fazer isto, ele colocou um teodolito a
300 metros do edifício e mediu um ângulo de 30°, como indicado na figura a seguir.
A luneta do teodolito está a 1 metro do solo. Considerando √3 = 1,73, a altura do edifício, em metros, é:
A) 150
B) 151
C) 173
D) 174
E) 200
2) Do quadrilátero ABCD da figura a seguir, sabe-se que: os ângulos internos de vértices A e C são retos; os
ângulos CDB e ADB medem, respectivamente, 45° e 30°; o lado CD mede 2dm.
Então, os lados AD e AB medem, respectivamente, em dm:
A) √6 e √3
B) √5 e √3
C) √6 e √2
D) √6 e √5
E) √3 e √5
3) Uma escada de 2m de comprimento está apoiada no chão e em uma parede vertical. Se a escada faz 30°
com a horizontal, a distância do topo da escada ao chão é de:
A) 0,5 m
B) 1 m
C) 1,5 m
D) 1,7 m
E) 2 m
4) Considere os triângulos retângulos PQR e PQS da figura a seguir. Se RS = 100, quanto vale PQ?
A) 100√3
B) 50√3
C) 50
D) (50√3)/3
E) 25√3
1
5) Duas circunferências são tangentes entre si e aos lados de um ângulo. Se R é o raio da maior, r é o raio da
menor e o ângulo mede 60°, então R vale:
A) (3√3)r/2
B) 2√3r
C) 3√3r
D) 2r
E) 3r
6) A seguir está representado um esquema de uma sala de cinema, com o piso horizontal.
De quanto deve ser a medida de AT para que um espectador sentado a 15 metros da tela, com os olhos 1,2
metros acima do piso, veja o ponto mais alto da tela, que é T, a 30° da horizontal? Considere √3 = 1,7.
A) 15,0 m
B) 11,7 m
C) 10,0 m
D) 9,7 m
E) 8,5 m
7) Em uma rua plana, uma torre AT é vista por dois observadores X e Y sob ângulos de 30° e 60°com a
horizontal, como mostra a figura a seguir.
Se a distância entre os observadores é de 40m, qual é aprox. a altura da torre? (Utilize √2 = 1,4 e √3 = 1,7).
A) 30 m
B) 32 m
C) 34 m
D) 36 m
E) 38 m
8)Uma pessoa encontra-se num ponto A, localizado na base de um prédio, conforme mostra afigura adiante.
Se ela caminhar 90 metros em linha reta, chegará a um ponto B, de onde poderá ver o topo C do prédio, sob
um ângulo de 60°. Quantos metros ela deverá se afastar do ponto A, andando em linha reta no sentido de A
para B, para que possa enxergar o topo do prédio sob um ângulo de 30°?
A) 150
B) 180
C) 270
D) 300
E) 310
9)Observe a bicicleta e a tabela trigonométrica.
Os centros das rodas estão a uma distância PQ igual a 120 cm e os raios PA e QB medem, respectivamente,
25 cm e 52 cm.De acordo com a tabela, o ângulo AÔP tem o seguinte valor:
A) 10°
B) 12°
C) 13°
D) 14°
2
10) Um barco navega na direção AB, próximo a um farol P, conforme a figura a seguir.
No ponto A, o navegador verifica que a reta AP, da embarcação ao farol, forma um ângulo de 30° com a
direção AB. Após a embarcação percorrer 1.000 m, no ponto B, o navegador verifica que a reta BP, da
embarcação ao farol, forma um ângulo de 60° com a mesma direção AB. Seguindo sempre a direção AB, a
menor distância entre a embarcação e o farol será equivalente, em metros, a:
A) 500
B) 500√3
C) 1.000
D) 1.000√3
11) Um foguete é lançado com velocidade igual a 180 m/s, e com um ângulo de inclinação de 60°em relação
ao solo. Suponha que sua trajetória seja retilínea e sua velocidade se mantenha constante ao longo de todo o
percurso. Após cinco segundos, o foguete se encontra a uma altura de x metros, exatamente acima de um
ponto no solo, a y metros do ponto de lançamento. Os valores de x e y são, respectivamente:
A) 90 e 90√3
B) 90√3 e 90
C) 450 e 450√3
D) 450√3 e 450
12) De dois observatórios, localizados em dois pontos X e Y da superfície da Terra, é possível enxergar um
balão meteorológico B, sob ângulos de 45° e 60°, conforme é mostrado na figura abaixo.
Desprezando-se a curvatura da Terra, se 30 km separam X e Y, a altura h, em quilômetros, do balão à
superfície da Terra, é:
A) 30 - 15√3
B) 30 + 15√3
C) 60 - 30√3
D) 45 - 15√3
E) 45 + 15√3
13) Observe a figura a seguir e determine a altura h do edifício, sabendo que AB mede 25 m e cos = 0,6 .
A) 22,5 m
B) 15 m
C) 18,5 m
D) 20 m
14) Em certa hora do dia, os raios do Sol incidem sobre um local plano com uma inclinação de 60o em relação
à horizontal. Nesse momento, o comprimento da sombra de uma construção de 6m de altura será,
aproximadamente:
A) 10,2m
B) 8,5m
C) 5,9m
D) 4,2m
E) 3,4m
15) Um barco atravessa um rio num trecho onde a largura é 100m, seguindo uma direção que forma um
ângulo de 30o com uma das margens. A distância percorrida pelo barco para atravessar o rio é:
A) 100m
B) 200m
C) 200/√3m
D) 150m
E) 250m
3
16) Um observador, no ponto A, vê o topo de um poste (B) e o topo de um prédio (C), conforme a figura.
Se as alturas do poste e do prédio são, respectivamente, 6√3 m e 30 m, então a distância x é, em metros:
A) 15√3 − 18
B) 15√3 −10
C) 30√3 – 24
D) 30√3 – 20
E) 30√3 −18
17) A figura representa um barco atravessando um rio, partindo de A em direção ao ponto B. A forte
correnteza arrasta o barco em direção ao ponto C, segundo um ângulo de 60o. Sendo a largura do rio de
120m, a distância percorrida pelo barco até o ponto C, é:
A) 240√3m
B) 240m
C) 80√3m
D) 80m
E) 40√3m
18) Uma torre vertical é presa por cabos de aço fixos no chão, em um terreno plano horizontal, conforme
mostra a figura. Se A está a 15m da base B da torre e C está a 20m de altura, comprimento do cabo AC é:
A) 15m
B) 20m
C) 25m
D) 35m
E) 40m
19) Uma escada que mede 4m tem uma de suas extremidades aparada no topo de um muro, e a outra
extremidade dista 2,4m da base do muro. A altura do muro é:
A) 2,3m
B) 3,0m
C) 3,2m
D) 3,8m
20) Um observador, no ponto O da figura, vê um prédio segundo um ângulo de 75°. Se esse observador está
situado a uma distância de 12m do prédio e a 12m de altura do plano horizontal que passa pelo pé do prédio,
então a altura do prédio, em metros, é:
A) 4(3 + √3)
B) √3
C) √3/2
D) 6(√2 + 2)
E) 1/2
Gabarito
1D 2C 3B 4B 5E 6D 7C 8C 9C 10B 11D 12D 13D 14E 15B 16E 17B 18C 19C 20A
4