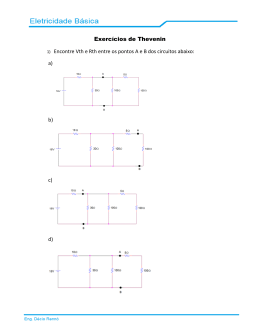
Eletricidade A - ENG04474
AULA V
Equivalentes de Thevenin e Norton
i
R1
R1
+
v
-
Circuito de um bipolo linear
v=i+ ou i =  v + 
 Um bipolo é equivalente a outro quando a
relação entre tensão e corrente em seus
terminais é exatamente a mesma.
Circuito qualquer
Que outro
circuito teria a
equação v=i+
Teorema de Thevenin
 Um circuito linear qualquer visto por quaisquer dois terminais
onde a relação entre tensão e corrente é determinada por uma função
linear algébrica é equivalente a um bipolo constituído por uma fonte
de tensão (Vth) em SÉRIE com um resistor (Rth).
 Vth é a tensão a circuito aberto entre A e B.
 Rth é a resistência equivalente entre A e B com as
FONTES INDEPENDENTES mortas
v=i+
i
R1
R1
Circuito resistivo contendo fontes
dependentes e independentes
+
v
-
Rth
A

+
Vth
-
B
v=Rthi+Vth
i
+
v
-
A
B
Bipolo Equivalente - Teorema de Thevenin
 Equivalente Thevenin é um bipolo equivalente a outro bipolo
 Pode ser empregado para representar um circuito linear em que
não se está interessado em suas correntes e tensões
 Pode ser empregado para simplificar um circuito linear maior
 Exemplo

R1
R2
Rth
+
V1
I1
R4
3i
ix
100ix
R3
-
+
-
i
R7
R6
+
vx
-

R5
ix
+
100ix
R3
Vth
R6
+
vx
-
R5
Bipolo Equivalente - Teorema de Thevenin
 Determinando Vth
 Determinar a TENSÃO a CIRCUITO ABERTO entre os
terminais do bipolo
R1
i =A 0
3
 Exemplo - Vth
i
R1
3
A
+
R3
1
-
A
+
V1
10V
R2
2
-
Rth
+
v
-B
i
A
+
-
Vth
4V
+
v
-B
V1
10V
R4
4
+
vz
-
B
Vth =
R2
R1+R2
Rth
R4
4
-
ABERTO
Bipolo a circuito aberto
R3
1
+
vz
-
R2
2
+
vCIRC. = Vth
V1 =
-
3+2
10 = 4V
i=0
A
A
+
2
Vth
4V
B
+
vCIRC. = Vth
-
ABERTO
Bipolo Equivalente - Teorema de Thevenin
 Exemplo - Vth?
R3
4
R1
5
+
R4
3
iz
V1
25V
I1
3A
R2
20
-
R3
4
R1
5
+
-
V1
25V
R2
20
I1
3A
+
R5
10
V2
10V
+

-
-
i=0
B
iz
Vth
R5
10
32V
+
I2
5A
R1
5
R2
20
I1
3A
V2
10V
-
R3
4
R3
4
A
+
Vth 
-
R4
3
Rth

- vR3 +
Ieq
8A
5A
Req
4
+
vReq
-
i=0
A
+
Vth
B
Vth = vR3 + vReq
Vth = R3 i + Req(i + Ieq)
Vth = 4.0 + 4.(0 + 8) = 32V
Bipolo Equivalente - Teorema de Thevenin
 Como determinar o valor de um Resistor???
idf
Amperímetro
+
vs
I
f
+
Rx
Voltímetro
V
Rx
-
-
Rx =
vsf
I
Rx =
V
idf
Bipolo Equivalente - Teorema de Thevenin
 Determinando Rth
 Matar TODAS as FONTES INDEPENDENTES do bipolo
 Alimentar os terminais A-B do bipolo com uma fonte de
tensão (V) ou corrente (I) de valor conhecido (qualquer valor).
• Se Fonte de Tensão (V)
– Determinar a corrente (idf) que a fonte fornece ao bipolo
Rth =
V
idf
bipolo
idf
+
V
Rth
-
• Se Fonte de Corrente (I)
– Determinar a tensão (vsf) sobre o bipolo
vsf
Rth =
I
bipolo
Rth
 Caso Particular
+
vsf
-
• Em circuitos onde existem apenas fontes independentes
– Matar todas as fontes independentes
– Determinar o resistor equivalente entre A-B usando equivalentes
série, paralelo e estrela-triângulo.
Rth = Resistor
Equivalente
I
Bipolo Equivalente - Teorema de Thevenin
 Exemplo - Rth
Método Geral - Fonte de Tensão Vx
i
R1
3
R1
3
R3
1
iR2 A
A
+
V1
10V
-
R2
2
+
v
-B
-
Vth
4V
+
v
-B
+
 Vx
R2
1
+
iR2 =
-
R4
4
Vx
R1
Vx
R2
idf = iR1 + iR2
Rth =
Vx
idf
=
1
1
R1
R3
1
A
+
1
iR1 =
Vx
B
R1
i
R2
2
V1 = 0
R4
4
idf = 
Rth
1,2
Rth
idf
iR1
+
1
= 1,2
R2
Somente Fontes Independentes
Caso Particular
R1
3
 Rth = R1//R2 =
R2
2
B



V1 = 0
A
Req
1
1
R1
+
1
R2
= 1,2
Bipolo Equivalente - Teorema de Thevenin
 Exemplo - Rth
 Caso Particular - Apenas Fontes Independentes
R3
4
R1
5
+
iz
V1
25V
I1
3A
R2
20
-
-
+
V2
10V
+

-
-
R2
20
I1I1
=0
3A
 Rth = R1//R2 + R3 =



V1 = 0
V1
25V
R5
10
R4
3
Rth
8
Vth
32V
iz
R5
10
R3
4
R1
5
+
R4
3
Req
1
1
R1
+
1
R2
+ R3 = 8 
+
-
V2
10V
Bipolo Equivalente - Teorema de Thevenin
 Exemplo - Rth
 Com Fontes Dependentes
• É necessário utilizar o Método Geral
 FONTES DEPENDENTES NÃO PODEM SER MORTAS
V2
8V2
i
V2
8V2
i
+
+
+ vz I1
4A
V1
10V
iV2
R3
10
R1
2
R2
2
-
+
+
-
V1= 0
V1
10V
iR1
iR2
I10
I1 =
+
Vx
R2
2
4A
-
-
-
i
iR2 =
R3
10
+ vz Vth
7,34V
idf
R1
2
+
V2
10V
i
Rth
1,6
+
2i
2i
+
-
Vx
R2
-idf + iR2 - i = 0  idf =
V2 = Vx = 8i
V2
10V
V
i= x
8
Rth =
Vx
idf
=
Vx
V
- x
8
R2
1
1
8
+
1
R2
= 1,6
Teorema de Norton
 Um circuito linear qualquer visto por quaisquer dois terminais
onde a relação entre tensão e corrente é determinada por uma função
linear algébrica é equivalente a um bipolo constituído por uma
fonte de Corrente (IN) em PARALELO com um resistor (RN).
 IN é a corrente de curto circuito entre A e B.
 RN é a resistência equivalente entre A e B com as
FONTES INDEPENDENTES mortas (IGUAL a Rth)
i
i
R1
R1
Circuito resistivo contendo fontes
dependentes e independentes
+
v
-
A

B
+
IN
RN
A
v
-
B
Bipolo Equivalente - Teorema de Norton
 Equivalente Norton é um bipolo equivalente a outro bipolo
 Pode ser empregado para representar um circuito linear em que
não se está interessado em suas correntes e tensões
 Pode ser empregado para simplificar um circuito linear maior
 Exemplo

R1
R2
Rth
+
V1
I1
R4
3i
ix
100ix
R3
-
+
-
i
R7
R6
+
vx
-

R5
ix
+
Vth
IN
-
100ix
R3
RN
R6
+
vx
-
R5
Bipolo Equivalente - Teorema de Norton
 Determinando IN
 Determinar a CORRENTE de CURTO CIRTUITO entre os
terminais do bipolo
R1
3
 Exemplo - IN
A
A
i
R1
3
+
R3
1
A
+
V1
10V
R2
2
-
+
v
-B
i
Rth
A
+
IN
Vth
4V
3,33A
-
RN
+
v
-B
R4
4
+
vz
-
-
V1
10V
+
v=0
-
R2
2
= IN
Circuito
B
Bipolo em curto circuito
IN =
V1
=
R1
R3
1
+
vz
-
iCurto.
10
3
= 3,33A
A
R4
4
A
+
IN
3,33A
RN
v=0
B
iCurto.
= IN
Circuito
Bipolo Equivalente - Teorema de Norton
 Exemplo - IN?
R3
4
R1
5
+
R4
3
iz
V1
25V
I1
3A
R2
20
-
R3
4
R1
5
+
-
V1
25V
R2
20
I1
3A
+
R5
10
V2
10V

Vth
IN
20V
4A
3,33A
-
-
R3
4
B
I2
5A
R1
5
R2
20
iz
+
A
+
v=0 IN
-
R4
3
Rth
I1
3A
RN
8
R5
10
+
V2
10V
-
R3
4
A

Ieq
5A
8A
Req
4
B
Req
(Req+R3)
4
IN = 8
=4A
(4+4)
IN = Ieq
A
IN
B
Relação entre os Equivalentes de
Thevenin e Norton
i
A
R1
R1
+
v
-

i
i
Rth
A
A
+
v
-
+
Vth
-
B
Circuito resistivo contendo fontes
dependentes e independentes

+
IN
B
RN
v
-
B
Rth=RN
 Se i=0 (circuito aberto)
 v=Vth=INRN ou Vth=INRth
 Se v=0 (curto circuito)
 -i=IN=Vth/Rth ou IN=Vth/RN
Logo Rth ou RN também podem ser determinados a partir de Vth e IN
RTh  RN 
VTh
IN