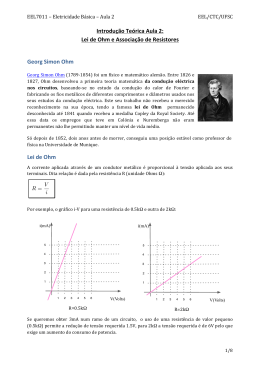
TIPOS DE CORRENTE ELÉTRICA
O modo como os eletrões se movem
determina o tipo de corrente
+
CORRENTE ELÉTRICA CONTÍNUA 
o fluxo de eletrões passa pelo fio
sempre no mesmo sentido
E
I
 sentido não convencional
ddp =(VA – VB)
1
CORRENTE ELÉTRICA ALTERNA
é aquela cuja sentido e a intensidade variam periodicamete
60 ciclos/ segundo
f = 60 Hz
2
Formas de onda de corrente contínua e corrente alterna
a) A corrente contínua (DC) é a
corrente que passa através de um
condutor ou de um circuito somente
num sentido.
V (t )  V0  diferença de potencial constante
I (t )  I 0
 corrente elétrica constante
b) Uma fonte de tensão alternada (tensão CA)
inverte ou alterna periodicamente a sua
polaridade.
 consequentemente, o sentido da corrente
alterna resultante também é invertido
periodicamente
V (t )  V0 sint
I t  
V t  V0 sin t


R
R
I t   I 0 sin t
(V0 tensãomáxima)
( I 0 correnteelétricamáxima)
3
VALOR EFICAZ
O calor desenvolvido numa resistência é independente do sentido de circulação da
corrente.
O valor eficaz corresponde à mesma quantidade de corrente ou tensão contínua capaz
de produzir a mesma potência de aquecimento
Os valores indicados nos aparelhos de medida de intensidade de corrente
(amperímetro) e de tensão (voltímetro) são os respetivos valores eficazes
Corrente elétrica eficaz
I0
I ef 
2
Tensão elétrica eficaz
V0
Vef 
2
Valor eficaz da corrente elétrica  é o
mesmo valor de corrente contínua capaz de
produzir a mesma quantidade de calor que a
corrente alterna e no mesmo recetor e
mesmo intervalo de tempo
I ef
4
ENERGIA ELÉTRICA E POTÊNCIA
Vimos que uma bateria é usada para criar uma corrente elétrica num condutor, há uma
transformação contínua da energia química na bateria em energia cinética dos eletrões e em
energia interna no condutor, tendo como consequência um aumento na temperatura do condutor

Análise da transferência de energia dum circuito
E
em que uma bateria é ligada a um resistor de
b
resistência R :
Supomos que uma carga positiva Q, sai do ponto a,
passando através da bateria e do resistor, e volta ao
ponto a
Ponto a  ponto de referência em que o potencial é zero
ab
V
Q
a
A energia potencial elétrica do sistema aumenta U  QV 
a energia química da bateria diminui da mesma quantidade.
c  d atravessa o resistor, e o sistema perde energia potencial elétrica durante colisões com os
átomos no resistor. A energia é transformada em energia interna  aumento do
movimento vibracional dos átomos no resistor e da temperatura.
ac ecd
nenhuma transformação ocorre porque desprezamos a resistência dos fios de
ligação.
Resultado líquido quando a carga retorna ao ponto a: parte da energia química da bateria
foi para o resistor e permanece nele como energia interna associada a vibração molecular.
5
O sistema perde energia potencial elétrica quando a carga Q atravessa o resistor:
dU d
dQ
 QV  
V  IV
dt dt
dt
Posteriormente o sistema recupera essa energia potencial, à custa da energia química da bateria,
quando a carga atravessa novamente a bateria
P  IV

representa a POTÊNCIA  taxa de energia fornecida ao resistor
 ou a qualquer outro dispositivo que transporte uma corrente elétrica I, e tem uma diferença
de potencial entre os seus terminais V.
Utilizando V=RI pode-se expressar a potência entregue ao resistor nas formas
PI R
2
ou
2

V 
P
R
 transformação de energia elétrica em energia
térmica . Energia perdida.
A potência fornecida a um resistor é frequentemente chamada de uma perda I 2 R
 a energia dissipada no condutor é o calor Joule ou o efeito é o efeito Joule
Unidade SI: watt (W) que corresponde a J/s
6
EXEMPLO DE UM CIRCUITO ELÉTRICO
sentido convencional da
corrente
7
ELEMENTOS DE UM CIRCUITO ELÉTRICO
I
Chave
+
-
Bateria
8
Exemplo: Uma lâmpada é classificada como sendo de 120 V / 75 W, o que significa que
a sua tensão de funcionamento pretendida de 120 V, tem uma potência de 75 W.
O brilho da lâmpada está relacionado com a tensão em que se liga a lâmpada. A
tensão nominal corresponde ao brilho normal. Com menor tensão que a nominal , o
brilho da lâmpada é mais fraco, e com maior tensão, ela pode queimar. Supomos que a
lâmpada é alimentada por uma fonte de 120 V em corrente contínua.
Qual é a corrente na lâmpada e a sua resistência?
Resolução
A corrente elétrica na lâmpada:
Sabemos que
P  IV

P
75 W
I

 0.625 A
V 120 V
A resistência elétrica da lâmpada:
V  RI

V
120 V
R

 192 
I
0.625 A
9
AS FONTES DE TENSÃO DE CORRENTE CONTÍNUA (DC) PODEM SER DIVIDIDAS EM
TRÊS CATEGORIAS:
Baterias  utilizam reações químicas
Geradores  transformam energia mecânica em elétrica
Fontes de alimentação:
 obtêm corrente contínua retificando a corrente alternada
 convertem a tensão variável numa tensão com valor fixo
FONTES DE FORÇA ELETROMOTRIZ (fem)
O dispositivo que mantém a tensão constante num circuito DC é chamado de fem
Símbolo 
Potencial
maior
A fonte deve realizar um trabalho dW sobre um
elemento de carga dq para que esta se desloque do
terminal (–) para o terminal (+)
dW

dq
Unidade da fem no SI: V
Potencial
menor
J
C
Na realidade a fonte tem uma resistência interna 
11
CÁLCULO DA CORRENTE DO CIRCUITO
Tensão nos terminais da fonte
V    rI
V  RI
e
  V  rI  RI  rI 
I
Se a fonte não tiver resistência interna (r=0) 
I

Rr

R
12
a) Diagrama do circuito com uma
fonte de fem  de resistência interna r
ligado a um resistor externo R .
(a)
b) Representação gráfica que mostra
como o potencial varia quando o
circuito é percorrido por uma
corrente.
(b)
13
RESISTORES EM SÉRIE
Uma mesma corrente passa através dos resistores ligados em série. A soma das
diferenças de potencial entre as extremidades dos resistores é igual diferença de
potencial aplicada:
V  R1 I  R2 I  I R1  R2 

V  Req I
Req  R1  R2
A resistência equivalente de três ou mais resistores em série é
Req  R1  R2  R3  ...   Ri
i
14
RESISTORES EM PARALELO
Os resistores ligados em paralelo estão submetidos a mesma diferença de potencial:
 1 1  V
V V
I  I1  I 2 

 V    

R1 R2
 R1 R2  Req
1
1
1
 
Req R1 R2
A resistência equivalente de três ou mais resistores em paralelo é
1
1
1
1
1



 ...  
Req R1 R2 R3
1 Ri
15
Exemplo 1
Um aquecedor de 1250 W é construído para operar sob uma tensão de 115 V.
(a) Qual será a corrente no aquecedor?
(b) Qual é a resistência da bobina de aquecimento?
(c) Que quantidade de energia térmica é gerada pelo aquecedor em 1 hora?
16
Exemplo 2
U
U
17
Exemplo 3
18
Exemplo 3 (continuação)
(i  q / t )

19
Exemplo 3 (continuação)
20
Exemplo 4. Calcular a resistência equivalente e a corrente que passa no circuito.
Temos: R3 em serie com R4 e com R5. Resulta em:
R6  R3  R4  R5
 (20  30  50)   100
No circuito resultante R6 ficou em paralelo com R2:

1
1
1
1
1




 R7  60 
R7 R6 R2 100 150
R7 está em série com R1, e é a
última simplificação:
Req  R1  R7
 (30  60)   90 
A corrente que passa no circuito 
V  Req I  I 
V 18 V

 0.2 A
Req 90 
REGRAS DE KIRCHOFF
Os resistores podem estar ligados de maneira que os circuitos formados não possam
ser reduzidos a um único resistor equivalente.
Para analisar tais circuitos mais complexos convém utilizar duas regras simples 
as duas Leis de Kirchhoff.
Estas leis são baseadas em princípios de conservação de energia e de carga
1ª LEI DE KIRCHOFF (OU LEI DOS NÓS) – a soma das correntes que entram em
qualquer nó é igual à soma das correntes que saem desse nó.
I
n
0
n
22
2ª LEI DE KIRCHOFF - a soma das diferenças de potencial em todos os elementos de
uma malha fechada do circuito é igual à zero, pois os pontos inicial e final são iguais.
 V
n
0
n
As regras seguintes mostram como cada queda de
potencial é usada nesse somatório.
Chama-se “queda de
potencial”, a diferença
de potencial entre dois
pontos de um circuito
sentido convencional da corrente para a fonte
I
V  
V  
V   IR
V   IR
23
Exemplo 1: Um circuito é constituído de três resistências, dois recetores e um
gerador. Determine:
a) o sentido da corrente elétrica;
b) a resistência elétrica equivalente do circuito;
c) a intensidade da corrente elétrica no circuito;
d) a ddp entre os pontos A e B.
Resolução:
a) Qual dos três dispositivos elétricos é o
gerador? É aquele com maior fem:  3  18 V
A corrente elétrica, portanto, vai do terminal negativo para o positivo. Isso faz
com que a corrente se movimente no sentido anti-horário pelo circuito e 1 e  2
representem recetores:
b) Como as resistências estão
associadas em série, a resistência
equivalente é dada por:
Req  R1  R2  R3  2 1  2  5 
24
c) a intensidade da corrente elétrica no circuito;
i
 3  1,   2,
Req
18  5  3

2A
5
d) a ddp entre os pontos A e B.
V   3  R3i   1,
 18  2  2i  5  9 V
V3  R3i
V
25
Exemplo: Circuito de várias malhas
26