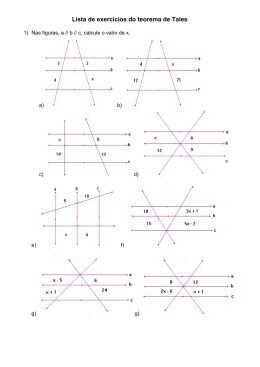
INSTITUTO DE APLICAÇÃO FERNANDO RODRIGUES DA SILVEIRA
Professor: Marcello Amadeo
Aluno(a): _______________________________________________ Turma: _______
LISTA 3 – Teorema de Tales
Teorema de Tales
Chamamos de feixe de paralelas um conjunto de retas paralelas de um plano,
B
ou seja, 𝐴𝐵 //
D
A
𝐶𝐷 // 𝐸𝐹 // 𝐺𝐻 .
F
C
H
E
G
Retas paralelas cortadas por uma transversal:
Considere que as distâncias entre duas retas consecutivas do feixe
acima seja iguais; se as duas transversais traçadas são paralelas
entre si, então as medidas dos segmentos determinados sobre cada
uma delas são congruentes.
Razão entre segmentos:
Dados dois segmentos AB e CD, chama-se razão entre AB e
CD , a razão dos
números que expressam a medida desses segmentos na mesma unidade.
Considere agora o caso em que as retas transversais
não são paralelas entre si. Na figura, representamos duas
retas paralelas r, s e t, e duas oblíquas m e n em relação ao
feixe de paralelas
Observando a figura, vemos que os segmentos
determinados sobre a transversal m são congruentes (iguais
a u) , e aqueles determinados sobre a transversal n são
iguais a u’.
A partir da figura acima, é possível compreender o
Teorema de Tales, enunciado a seguir:
TEOREMA DE TALES
Quando duas transversais interceptam um feixe de paralelas, os segmentos determinados nas
transversais são respectivamente proporcionais.
Na figura anterior, temos: AB = 3u e PQ = 3u’; AC = 5u e PR = 5u’; BC = 2u e QR = 2u’, isto nos mostra que:
AB AC BC
u


 . . . 
PQ PR QR
u'
1
CONSEQUÊNCIA
Toda paralela a um lado de um triângulo determina sobre os outros lados (ou seus prolongamentos) segmentos
proporcionais.
A
S
R
AR
S
B
AS

BR
CS

R
A
AB
AC
B
C
C
PROPRIEDADES
1) Toda paralela a um dos lados de um triângulo determina, nos outros dois lados, segmentos que são
proporcionais.
2) Se uma reta intercepta dois lados de um
então
ABC
nos pontos M e N, tais que
AM
AN
=
,
MB
NC
MN é paralelo ao lado BC.
TEOREMA DA BISSETRIZ INTERNA (TBI)
Em todo triângulo, a bissetriz interna relativa a um dos lados determina sobre ele segmentos proporcionais aos
outros dois.
A

AB
BD
B

AC
CD
C
D
TEOREMA DA BISSETRIZ EXTERNA (TBE)
Em todo triângulo, com a exceção do triângulo isósceles, a bissetriz externa a qualquer ângulo divide o lado
oposto, prolongado, em dois segmentos proporcionais aos outros lados.
A


AB
BD
B
C
D
2

AC
CD
EXERCÍCIOS:
01) A razão entre dois segmentos que medem,
respectivamente,
(A)
7
(B)
5
35 cm e
06) Um feixe de quatro paralelas determina, sobre uma
transversal, três segmentos que medem 5dm, y dm
e 11dm e sobre outra transversal, segmentos que
medem 10dm, 14dm e x cm. Os valores de x e y
são, respectivamente:
(A) 7dm e 22dm
7 cm é:
1
5
1
(D)
7
(B) 2,2dm e 2,8dm
(C)
(C) 22dm e 7dm
(D) 2,8dm e 2,2dm
07) Um feixe de três retas paralelas determina, sobre
uma transversal, os pontos M, N e O e, sobre
outros pontos M’, N’ e O’. Sabendo-se que MN =
3cm, NO = 2cm e M’O’ = 10cm,
M’N’ e N’O’
medem, respectivamente:
02) Sejam x e y as medidas de dois segmentos. A
razão do primeiro para o segundo é 2 .
5
Adicionando-se uma unidade a cada comprimento,
obtém-se dois segmentos cuja razão é 3 .Quais as
7
medidas dos segmentos, em centímetros?
(A) 6cm e 4cm
(B) 4cm e 6cm
(C) 7cm e 3cm
(D) 3cm e 7cm
08) São dados três segmentos AB, CD e EF que
medem, respectivamente, 4cm, 9cm e 24cm. Um
quarto segmento GH, que forma com os três uma
proporção nessa ordem, medirá:
03) Quais são as medidas, em metros, de dois
segmentos a e b cuja razão é 0,5, sabendo-se que,
se subtraímos uma unidade de cada uma das
medidas obtemos dois segmentos cuja razão é 0,4?
(A) 27cm
(B) 54cm
(C) 18cm
(D) 45cm
04) Na figura abaixo, as retas a, b e c são paralelas e r
 
 =
09) Na figura abaixo, as retas a, b, c e d são paralelas
e as retas u e v, trans-versal. Então, x e y
valem:
e s, transversais. Se med AB = 7cm, med BC
 
 
14cm e med A' B' = 10cm e med B'C ' = x cm, então
x é igual a:
r
(A) 10cm
(B) 12cm
(C) 15cm
(D) 20cm
A
B 7
C 14
a
(A) 12 e 5.
s
A’
10 B’
x C’
a
(B) 12 e 3.
b
(C) 12 e 4.
c
(D) 8 e 4.
8
b
c
4
x
u
v
y
6
2
10) Na figura abaixo, r // s // t e A’C’ = 15.
y valem, respectivamente:
05) Para determinar a altura de um edifício, seu zelador
usou um artifício. Mediu a sombra do prédio, que 6
metros, e mediu sua sombra, que deu 0,20 metros.
Como sua altura é de 1,60 metros, ele obteve, para
altura do prédio, o valor
(A) 24 m
(B) 36 m
(C) 42 m
(D) 48 m
d
Então, x e
a
b
(A) 3 e 5.
A’
A
(B) 9 e 6.
(C) 8 e 6.
(D) 6 e 9.
C
3
2
B
3
x
B’
y
C’
11) A figura abaixo mostra r // s // t. Sendo a e b
duas transversais, então x é igual a:
a
b
(A) 5.
r
(B) 4.
(C) 3.
(B) 8 e 12.
(C) 8 e 10.
(D) 9 e 10.
16) Na figura abaixo, a // b // c.
respectivamente:
x+5
x+ 1
s
(D) 2.
(A) 6 e 12
x+3
x
Então, x e y valem,
t
a
2
(B) 12 e 36
9
x
b
(C) 36 e 6
12) Na figura abaixo, a // b // c // d. Os valores
respectivos de x e y são:
r
(D) 6 e 36
c
s
(A) 2 e 10.
a
(B) 10 e 2.
x
4
17) Na figura abaixo, as retas a, b, c são paralelas e r
b
(C) 4 e 8.
(D) 5 e 10.
y
24
8
8
x+2
y5
c
6
BC = 14, A' B'
e s são transversais. Se AB = 7,
=
10
e
y
B'C ' = x,
então x é
igual a:
12
d
a
(A) 20
13) Duas transversais são cortadas por um feixe de
quatro paralelas. A primeira, nos pontos A, B, C e
D; a segunda, em A’, B’, C’ e D’. Sabendo que AB
= 3cm, CD = 8cm, B’C’ = 10cm e AD = 16cm, então
s
A’
(B) 15
C
B
A
r
c
b
B’
C’
(C) 12
(D) 10
A' B' e C ' D' medem, respectivamente:
(A) 16cm e 6cm.
18)
Na
figura
abaixo, se
(B) 5cm e 10cm.
(C) 6cm e 16cm.
AD
GH ,
(D) 8cm e 16cm.
A
x
(A) 7,5.
BC = 9cm e AD = 4cm,
x
5
//
vale:
14) Duas transversais partem de um mesmo ponto A e
encontram duas paralelas. A primeira corta as
paralelas em B e C, enquanto a segunda corta em
D e E. Se AB = 6cm,
F
D
5,2
4
H
G
(B) 5,0.
então AE mede:
(A) 6cm
(C) 4,5.
(B) 8cm
(D) 6,5.
(C) 9cm
(D) 10cm
19) No triângulo FGH (figura), sendo DE // GH, x é
igual a:
15) Num triângulo ABC, marcam-se os pontos D em
F
(A) 4,0.
AD
AB e E em AC , tais que DE // BC . Sendo
DB
4
=
e AC = 18, então AE e EC medem,
5
(B) 4,5.
x+3
(C) 5,0.
D
x
respectivamente:
(A) 10 e 8.
(D) 5,54.
G
4
10
E
6
H
26) No triângulo ABC da figura seguinte,
bissetriz do ângulo interno Ĉ . Se AD = 3cm, DB =
2cm e AC = 4cm, o lado BC do triângulo mede:
20) No triângulo da figura abaixo, AD // BC e EF é a
bissetriz do ângulo Ê . Então, y é igual a:
A
D
2
(C) 7
5
cm
2
7
c)
cm
2
8
d)
cm
3
b)
x
6
(B) 6
3
B
y
F
4
(D) 8
C
21) Os lados de um  ABC são AB = 4cm, AC = 5cm e
A
D
B
27) Na figura abaixo, ABCD é um retângulo e E é o
ponto médio de AD. O segmento FG passa pelo ponto
médio M de CE. Determine a razão entre os
comprimentos de GM e MF.
BC = 6cm. Sendo AD a bissetriz interna do ângulo
A, determine BD e
C
a) 3cm
E
(A) 5
CD é a
DC .
22) Na figura abaixo, AD é bissetriz de Â. Sendo BD
= 6 e CD = 7, então o valor de x é:
A
(A) 6,5.
(B) 5.
2x
x+5
(C) 6.
(D) 7.
B
C
D
∠𝐴𝐵𝐹 = ∠𝐹𝐵𝐶 = 45° e 𝐴𝐶𝐷𝐸
2
é um quadrado. Se 𝐴𝐵 = ∙ 𝐵𝐶 , determine
23) O perímetro de um triângulo é de 100m.
A
bissetriz do ângulo interno  divide o lado oposto
em dois segmentos de 16m e 24m. Então, os lados
desse triângulo medem, em metros:
28) Na figura abaixo,
a razão
(A) 24, 40 e 36.
𝐸𝐹
𝐹𝐷
3
.
(B) 20, 40 e 40.
(C) 25, 30 e 45.
(D) 40, 30 e 30.
24)Na figura abaixo, AD é bissetriz de Â.
vale:
Então, x
A
(A) 5,6.
(B) 6,4.
12
8
(C) 4,2.
x
9,6
C
(D) 7,1.
B
D
29) Na figura abaixo, há três quadrados de lados 9, 6 e
x. Determine o valor de x.
25) No triângulo da figura abaixo, AD é bissetriz.
Então, BC vale:
B
(A) 11,0
A
(B) 15,4
6,3
9
(C) 10,5
(D) 11,9
C
8
D
5