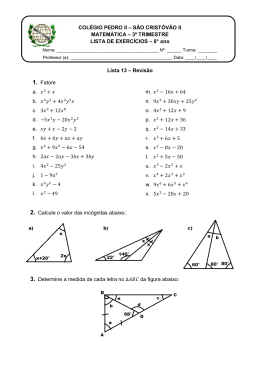
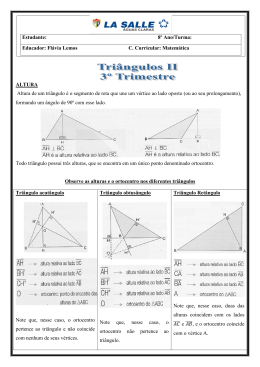
EF
8º
RECUPERAÇÃO
ALMIR
Ficha de exercícios de recuperação – 2º Trimestre
1) Observe a imagem e complete:
X
a) ̅̅̅̅, ̅̅̅̅ e ̅̅̅̅ são __________________________ do ΔXYZ.
b) ̂ , ̂ e ̂ são ______________________________ do ΔXYZ.
c) X, Y e Z são ______________________________do ΔXYZ.
Y
Z
2) Complete, usando mediana, bissetriz ou altura:
3) Observe a figura e complete:
a) A altura relativa a ̅̅̅̅ é _________________________ .
b) A altura relativa a ̅̅̅̅ é _________________________ .
c) A altura relativa a ̅̅̅̅ é _________________________ .
4) O segmento ̅̅̅̅é uma mediana do ΔEFG. Calcule o perímetro do triangulo.
FOLHA REC 2 TRI
5) Os ângulos ̂ e ̂ do ΔABC medem respectivamente, 80° e 60°. Sabendo que I é o
incentro do ΔABC, qual é a medida de IÂB?
6) Calcule a, sabendo que:
a) ̅̅̅̅ é uma altura e ̅̅̅̅ bissetriz de FÊG.
b) I é o incentro do ΔMNP.
7) Um triângulo equilátero tem 45 cm de perímetro. Qual o comprimento de cada lado?
Quanto mede cada ângulo?
8) Um triângulo isósceles tem 150 cm de perímetro. A base mede 30 cm. Qual é o
comprimento de cada um dos outros lados?
FOLHA REC 2 TRI
9) Determine as medidas dos ângulos de um triângulo retângulo isósceles.
10) Nas figuras, os ΔABC são isósceles de base ̅̅̅̅. Calcule o perímetro de cada um.
a)
b)
11) O ΔABC é isósceles e o ângulo do vértice oposto a base é ̂. Calcule x e y.
12) O ângulo externo adjacente a base de um triângulo isósceles mede 126°. Quais são as
medidas dos ângulos do triângulo?
13) Na figura, o ΔDEF é isósceles de base ̅̅̅̅, e ̅̅̅̅ é uma bissetriz. Calcule x, y e z.
FOLHA REC 2 TRI
14) Num triângulo retângulo, os ângulos agudos são congruentes. Quais as medidas dos
ângulos desse triângulo?
15) Na figura, o ΔABC é congruente ao ΔRST. Calcule o perímetro de cada um.
16) Na figura, o triângulo ABO é congruente ao triângulo DEO. Determine os valores de x e
y.
17) Usando as designações LLL, ALA, LAL, LAAo, indique qual o caso de congruência.
FOLHA REC 2 TRI
18) Dado que o ΔABV é isósceles de base ̅̅̅̅ e ΔVAC ≡ ΔVBC, calcule o perímetro do
ΔABC.
19) Prove a congruência dos triângulos na figura abaixo.
20) No quadrado, M é o ponto médio de ̅̅̅̅. Prove que ̅̅̅̅̅ ≡ ̅̅̅̅̅.
21) Determine a medida de cada um dos ângulos no ∆ABC.
22) O ângulo interno ̂ mede 56º e o ângulo interno ̂ mede 76º. O segmento ̅̅̅̅ é bissetriz
do ângulo interno ̂ e o segmento ̅̅̅̅ é a bissetriz do ângulo ̂ . Determine as medidas x e
y indicadas.
FOLHA REC 2 TRI
23) N afigura seguinte, ̅̅̅̅ é altura relativa ao lado ̅̅̅̅ do triângulo ABC. Nessas condições,
determine as medidas x e y indicadas na figura.
24) O triângulo da figura é isósceles, com ̅̅̅̅
determine as medidas x e y indicadas.
̅̅̅̅ . Se ̅̅̅̅ é a bissetriz do ângulo ̂ ,
25) Em um triângulo isósceles, o ângulo oposto à base corresponde aos
ângulo da base. Determine as medidas dos três ângulos desse triângulo.
da medida do
26) Na figura seguinte, temos r / / s. Sabendo que o triângulo AMN é isósceles, determine as
medidas x e y indicadas.
FOLHA REC 2 TRI