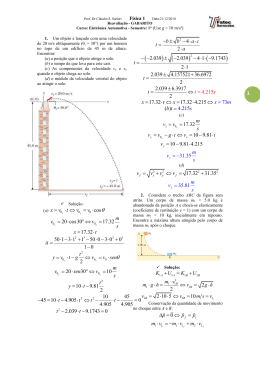

Ao lançarmos um corpo horizontalmente, a partir de
uma certa altura do solo, notamos que ele descreve
uma curva, onde se a resistência do ar for desprezível,
esta curva será um arco de parábola.

V

g
Sy
Sx
Movimento Horizontal : Movimento Uniforme
Movimento Vertical: Movimento Uniformemente Variado.
QUAL CHEGARÁ PRIMEIRO AO SOLO?

V
1
2
3

V
1
2
3

Pense!!!
I) Se no local do lançamento não
houvesse gravidade e nem
resistência do ar, o corpo
seguiria horizontalmente em
movimento uniforme.
II) Como há gravidade, o corpo
cairá simultaneamente em
queda livre, ou seja, realizará
um MUV na vertical, e ao
mesmo tempo, um MU na
horizontal.

Ao ser disparado de uma altura h, com uma velocidade
v0 , sob a ação exclusiva da gravidade g, o objeto toca
o solo após um tempo de queda (t) atingindo um
alcance horizontal (D ou A).
Queda Livre (eixo y)
Movimento Uniforme (eixo x)

Atenção!!!
Para calcular a velocidade que o móvel atinge em seu vôo
parabólico depois de um certo instante (t), basta fazer
a adição vetorial das componentes da velocidade (vy e
vx).
Lançamento oblíquo no vácuo
O lançamento oblíquo é uma composição de dois
movimentos:
•Movimento horizontal: Movimento Uniforme.
•Movimento Vertical: Movimento
Uniformemente Variado, sujeito a
aceleração gravitacional (g).
De acordo com o princípio de independência
dos movimentos (Galileu), cada um dos
movimentos ocorre independente do outro.
REVISANDO PROJEÇÃO DE VETORES
y
Vy

V

Vx
Vx  V . cos( )
Vy  V .sen( )
x
g
V0
Voy
SY
θ
V0x
SX
V0 x  V0 . cos
Voy  V0 .sen
PROPRIEDADES
Vy
Vy
V0x
g
V0x
V0x
Voy
V0x
V0x
Vy
V0x
V0x
Vy
Vy
•A componente horizontal da velocidade
permanece constante.
•A componente vertical da velocidade
diminui até atingir a altura máxima e
aumenta da altura máxima até voltar ao
solo.
•Na altura máxima a velocidade da
partícula é mínima, mas não é nula.
Qual corpo terá maior alcance?
60º
30º
•Para ângulos complementares (α + β = 90º)
o alcance será o mesmo.
g
α
45º
β
•Para ângulo de lançamento de 45 º o alcance
será máximo (com a mesma velocidade
inicial).