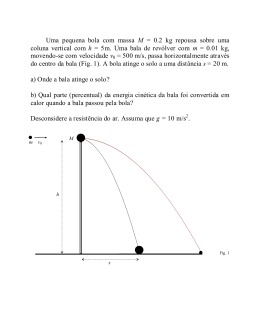
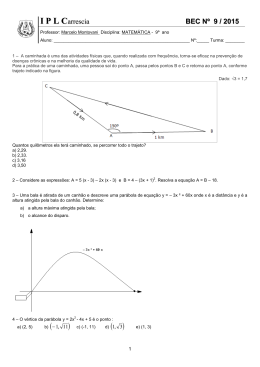
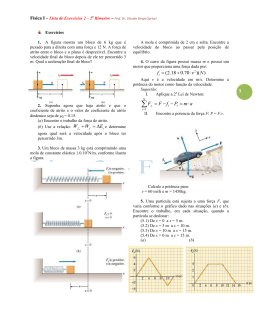
Prof. Dr Cláudio S. Sartori
Física 1
Data:21/12/2010
Reavaliação - GABARITO
Curso: Eletrônica Automotiva - Semestre: 1° (Use g = 10 m/s²)
1. Um objeto é lançado com uma velocidade
de 20 m/s obliquamente (θi = 30°) por um homem
no topo de um edifício de 45 m de altura.
Encontrar:
(a) a posição que o objeto atinge o solo.
(b) o tempo de que leva para este cair.
(c) As componentes da velocidade vx e vy
quando o objeto chega ao solo.
(d) o módulo da velocidade vetorial do objeto
ao atingir o solo.
t
t
b  b 2  4  a  c
2a
  2.039  
 2.039 
2
 4 1  9.1743
2 1
2.039  4.157521  36.6972
t
2
2.039  6.3917
t
 t  4.215s
2
x  17.32  t  x  17.32  4.215  x  73m
(b)t  4.215s
(c)
m
s
vy  v0 y  g  t  vy  10  9.81 t
vx  v0x  17.32
vy  10  9.81 4.215
v y  31.35
m
s
(d)
v f  vx2  vy2  v f  17.322  31.352
v f  35.81

(a)
Solução:
x  v0x  t  v0x  v0  cos 
v0x  20  cos30  v0x  17.32
m
s
m
s
2. Considere o trecho ABC da figura sem
atrito. Um corpo de massa m1 = 5.0 kg é
abandonado da posição A e choca-se elasticamente
(coeficiente de restituição e = 1) com um corpo de
massa m2 = 10 kg, inicialmente em repouso.
Encontre a máxima altura atingida pelo corpo de
massa m1 após o choque.
x  17.32  t
50 1  3 12  13  50  0  3  02  03
a
1 0
2
t
y  v0 y  t  g  v0 y  v0  sen
2
 Solução:
m
v0 y  20  sen30  v0 y  10
K
1 A  U1 A  K1B  U1B
s
m1  v12B
t2
m

g

h

 v1B  2 g  h
y  10  t  9.81
1
2
2
v  2 10  5  v1B  10 m s  v1
10
45
45  10  t  4.905  t 2  t 2 
t 
 0 1B
Conservação da quantidade de movimento
4.905
4.905
no
choque
entre A e B:
t 2  2.039  t  9.1743  0
 


p  0  p f  pi
i
m1  v1i  m1  v1f  m2  v2 f
1
Prof. Dr Cláudio S. Sartori
Física 1
Data:21/12/2010
Reavaliação - GABARITO
Curso: Eletrônica Automotiva - Semestre: 1° (Use g = 10 m/s²)
5 10  5  v1f  10  v2 f
2.5  0.008
10
2
0.008
2 1
m
km
km
vi  1402.01  1.4
 389
s
s
h
 vi 
10  v1 f  2  v2 f
v1 f  v2 f
e 1
10
v1 f  v2 f  10
1
v1 f  2  v2 f  10

 v1 f  v2 f  10
20
3v2 f  20  v2 f  m s
3
v1 f  10  v2 f  v1 f  10 
m1  g  h f 
hf 
10 3
2
20
10
 v1 f  m s
3
3
m1  v 2f1
2
4. Um bloco de 6 kg é abandonado do alto de
uma rampa como ilustra a figura a seguir. Não há
atrito entre o bloco e o plano.
 hf 
2
 hf 
2 10
h f  0.556m
v 2f1
2g
10
m
18
3. Uma bala de 8 g é atirada na direção de um
bloco de massa 2.5 kg, como mostra a figura:
Encontre a componente centrípeta e
tangencial da aceleração do bloco no ponto P
indicado e o módulo da aceleração resultante.

Solução:
Fazendo a conservação da energia, temos:
K A  U A  KP  U P
m g h 
m  vP2
 m g  R
2
2
m
  vP
m
  g  R  vP  2 g   h  R 
2
m
vP  2 10   5  2   vP  60
s
m
  g h 
O bloco está sobre uma mesa de 1 m de
altura e não há atrito sobre a mesa. A bala se aloja
no bloco e o conjunto bloco-bala cai a 2.00 m da
mesa. Determine a velocidade que o bloco chega
ao chão e a velocidade inicial da bala.
 Solução:
O bloco está sobre uma mesa de 1 m de altura e não há
atrito sobre a mesa. A bala se aloja no bloco e o conjunto blocobala cai a 2.00 m da mesa. Determine a velocidade inicial da
bala.
mM
m  vi   m  M   v f  vi 
vf
m
1
d  vf t  h  g t2
2
2h
d
g
t
 vf   vf  d 
g
t
2h
 vi 
M m
g
d 
m
2h
acpP
v2
 P  acp 
r

60

2
2
 acp  30
m
s2
No ponto P o bloco é liberado do contato
com a rampa; portanto, a aceleração tangencial é g.
aT   g
m
s2