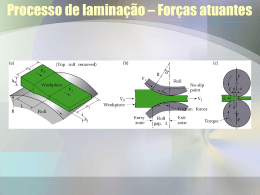
PUC-GO
ENGENHARIA DE PRODUÇÃO
Disc.: Processos de Fabricação II
Prof. Jorge Marques
Aulas 8
Processos de Conformação Mecânica
LAMINAÇÃO – parte 1
Referências:
CHIAVERINI, V. Tecnologia Mecânica. Vol. II
Telecurso 2000. Processos de Fabricação.
BRESCIANI, E. F. et. al. ; Conformação plástica dos metais.
CONCEITOS
 Laminação é um processo de conformação que
consiste na passagem de um corpo sólido entre
dois cilíndricos que giram à mesma velocidade
periférica, mas em sentido contrário, forçando-o a
reduzir espessura.
 Para se obter uma determinada dimensão do
corpo, deve-se submeter a peça a sucessivos
passes através dos cilindros, com distâncias entre si
decrescentes.
ILUSTRAÇÃO
FORÇAS E RELAÇÕES
 Na laminação a passagem da peça pelos cilíndricos
ocorre através da ação da força de atrito que atua
na superfície de contato entre peças e os
cilíndricos. Essa força é proporcional ao ângulo de
contato.
 O volume do material se mantem praticamente
constante; pois, a variação de volume por
eliminação de “microbolhas” é desprezível;
Volume Entrada = Volume de Saída
FORÇAS E RELAÇÕES
FORÇAS E RELAÇÕES
• O arraste ocorre por atrito. Então, caso o ângulo de
ataque (α) seja demasiadamente grande, o cilindro
desliza sobre a peça e não haverá laminação.
• É preciso que:
tgα < µ
α < arctgµ
µ = coeficiente de atrito entre o material a ser
laminado e o cilindro de laminação
RELAÇÕES E FORÇAS
Volume de entrada = Volume de Saída
ℎ𝑒𝑏𝑒𝑙𝑒 = ℎ𝑠𝑏𝑠𝑙𝑠
𝒉, 𝒃 e 𝒍 são, respectivamente a altura (espessura), a
largura e o comprimento. Os índices ees referem-se a
posição (entrada e saída, respectivamente) de um
determinado volume do material em laminação.
Sendo o comprimento 𝒍 por unidade de tempo igual a
velocidade (v) e desprezando-se a variação da largura,
tem-se:
ℎ𝑒𝑣𝑒 = ℎ𝑠𝑣𝑠
Nota: a largura é geralmente controlada e mantida constante.
RELAÇÕES E FORÇAS
FORÇAS E RELAÇÕES
FORÇAS E RELAÇÕES
Desenho Esquemático do sistema de acionamento de um laminador
Fonte: http://www.maxwell.lambda.ele.puc-rio.br/10090/10090_3.PDF
Força de Laminação
A determinação exata das forças necessárias para a laminação
é muito complexa. Modelos matemáticos foram desenvolvidos
para isso. Uma das Fórmulas é a de Dieter (1976):
2
𝑏 𝑄
𝜇𝑅𝛼
𝐹=
𝜎𝑒𝑠𝑐
𝑒 − 1 𝑅(∆ℎ)
𝑄=
𝑄
∆ℎ
3
𝑇 = 𝐹 𝑅(∆ℎ)
𝑃 = 2𝜋𝑛𝑇
𝐹 = força média de laminação (N).
𝜎𝑒𝑠𝑐 = tensão de escoamento do material laminado(N/mm²).
𝑏 = largura da placa (mm).
𝑅 = raio do cilindro de laminação.
𝜂 = rendimento do sistema de transmissão.
𝑇 = torque de laminação.
𝑃 = potência da laminação.
Exercícios
1) Num passe de laminação, deseja-se reduzir de 50 mm
para 38 mm a espessura de uma placa, cujo comprimento
inicial é 1200 mm. Sendo µ = 0,28 o coeficiente de atrito
entre o cilindro e o metal a ser laminado e 𝑣𝑒 = 5 m/s a
velocidade de entrada nos laminadores.
Pede-se para determinar:
a) O máximo ângulo de ataque possível.
b) O diâmetro mínimo dos cilindros de laminação.
c) A velocidade de saída.
d) O comprimento final do produto laminado.
Exercícios
2) Reconsidere o exercício anterior e determine a força
necessária de laminação; dados:
• Largura da placa = 200 mm
• 𝜎𝑒𝑠𝑐 = 350 N/mm²
• 𝛼 = 0,8𝛼𝑚á𝑥 (em radianos)
• 𝑅 = 𝑅𝑚𝑖𝑛 (calculado no exercício anterior)