Introdução ao
ensino das funções:
Gráficos
Autores: Rosana Maria Mendes
Karine Angélica de Deus
Iara Letícia Leite de Oliveira
Simone Uchôas Guimarães
Ricardo de Almeida Souza
Colaborador:
José Antônio Araújo Andrade
O recurso gráfico é muito utilizado para
representar relações entre grandezas.
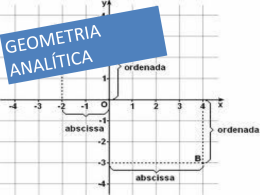
Para construirmos gráficos utilizamos
o sistema cartesiano ortogonal.
Para construirmos gráficos utilizamos
o sistema cartesiano ortogonal.
Eixo das abscissas
Para construirmos gráficos utilizamos
o sistema cartesiano ortogonal.
Eixo das ordenadas
O gráfico de uma função é o conjunto de
todos os pares ordenados (x, y) onde x
pertence D e y pertence a Im.
É lido na reta
graduada
horizontal, ou
seja, no eixo das
abscissas.
(x, y)
É lido na reta
graduada
vertical, ou seja,
no eixo das
ordenadas.
Chamamos de par ordenado porque a
ordem deles é importante.
Exemplo 1
Construir o gráfico da função
por
, onde
x
f(x) = x+2
(x,y)
, dada
.
Exemplo 2
Construir o gráfico da função
, dada por
Podemos observar um gráfico e identificar se ele
representa ou não uma função.
Para isso basta termos em mente que:
Uma relação será uma função se todos
elementos do domínio tiver um único
correspondente no contradomínio, ou seja, a
imagem.
Considerando que o D(f)= R e CD(f)=R então
analisemos alguns gráficos:
Cada elemento
do domínio
possui uma
única imagem.
Logo, esse
gráfico
representa
uma função.
Há um elemento
no domínio,
x = 3,
que não possui
uma imagem.
Logo, o gráfico
não representa
uma função.
Existem elementos no domínio que possuem mais
de um correspondente no contradomínio. Logo, o
gráfico não representa uma função
Representa uma função pois, cada elemento do
domínio possui uma única imagem.
As abscissas desses
pontos são o
{-2, -1, 0, 1, 2 e 3}.
Logo, o
D(f) = {-2, -1, 0, 1, 2, 3}.
O gráfico é constituído por
seis pontos.
As ordenadas desses
pontos são o
0, 1, 2, 3 e 4, logo, a
Im(f) = {0, 1, 2, 3, 4}.