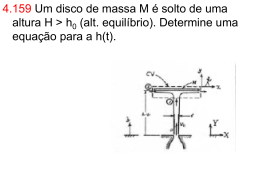
• -Uma bomba retira água de um resevatório
através de um tubo de aspiração de 150 mm
de diâmetro. A extremidade do tubo de
aspiração está 2 m abaixo da superfície livre
do reservatório. O manômetro no tubo de
descarga (2m acima da superfície do
reservatório) indica 170 kPa. A velocidade
média no tubo de descarga é de 3 m/s. Se a
eficiência da bomba for de 75% , determine
a potência necessária para acioná-la.
EM 461 – Prof. Eugênio Rosa
Qual é a potência
necessária para
bombear uma vazão Q?
d1=
150mm
170kPa
d2=
75mm
Z1=2 m
wshaft
Considerações:
1. D reserv. >> d tubulação
2. Vel. Reserv.  0
EM 461 – Prof. Eugênio Rosa
V~0
V2=3m/s
Exemplo.– Um tanque
grande contendo um
fluido incompressível
tem sua válvula aberta
para atmosfera em t = 0.
Considere a altura de líquido constante , que a
velocidade no interior do tanque é desprezível
e o escoamento se dá sem atrito. Modele o
escoamento no trecho reto de tubo que liga o
tanque a atmosfera.
EM 461 – Prof. Eugênio Rosa
Eq. Energia x Q. Movimento
• Para escoamentos incompressíveis, sem
transferência de calor (adiabáticos) e em
regime permanente, a Equação da
Energia e a Equação de Quantidade de
Movimento são Linearmente
dependentes.
• Consequência: pode-se usar tanto uma
quanto outra para resolver os problemas.
EM 461 – Prof. Eugênio Rosa
Ex– O carro de massa M parte do repouso propelido pelo jato
(Vj, Aj e r). O jato atinge o carro e é defletido num ângulo de 180o.
A) Determine a velocidade em função do tempo e a aceleração.
S.C.
2
U
Z
Vj
Aj
r
1
M
X
S.C. não deformável, Vb =0, mas que se desloca com
velocidade U(t)
Resposta:
A) U/Vj = t*/(1+t*) onde t* =t/t e t = (M/2)/(rAjVj)
EM 461 – Prof. Eugênio Rosa
Velocidades Relativas x Absolutas
S.C.
2
U
Vj
Aj
r
Z
1
M
X
Velocidade de um referencial que se move com o carro:
r
Vr1 
 V  U  ˆi
j
Relação entre Vr e VI
e
r
Vr2    Vj  U  ˆi
VI = Vr + U
r
V1   Vj  U   U  ˆi  Vjˆi e
r
V2     Vj  U   U  ˆi   2U  Vj  ˆi
EM 461 – Prof. Eugênio Rosa
  
VI2
VI2
VI2
d 
P 
P 
& W
&
& Q
 gz     u 
 gz     u 
 gz    m
r  u 
shaft
dt  
2
2
r
2
r


  
2 
1 
Isotérmico (u=0), P = Patm sem transferência de calor e
trabalho na S.C.:
d  VI2   VI2   VI2  
& 0
   
 
 m
r
dt  2   2  2  2 1 
d  VI2 
dU
r


MU
dt  2 
dt
Variação E.K.
dentro do V.C.:
Fluxo E.K.
cruza a S.C.
  2U  V
 V   V  
j

&

m


 


2
 2 2  2 1 

2
I
2
I
EM 461 – Prof. Eugênio Rosa
Vj2 
 r  Vj  U  A j

2 

dU
2r  Vj  U  A j  M
dt
2
Eq. Final

2
• Ex. – Determine a freqüência natural de oscilação de um
tubo em U. Considere a altura média do líquido em h0; a
área da seção transversal do tubo A e a distância entre
pernas de L.
z2
Vb
n
n
• Volume do sistema:
S.C.
V = (2h0+L)A
Vb
z1
h0
• Velocidade do fluido:
V = dz/dt = Vb
Re sposta:
L
d 2Z
Z

g
0
2
dt
h0
Z( 0 )  Z 0
EM 461 – Prof. Eugênio Rosa
dZ / dt t  0  0
Exemplo 3 – Um jato de água emerge de um orifício com
área A e possui uma velocidade Vo. A componente
horizontal do jato permanece constante a medida que o
jato é defletido pela gravidade. Determine a velocidade
resultante do jato, a distância h e a sua área transversal
numa seção com 45º de inclinação.
EM 461 – Prof. Eugênio Rosa
Exemplo I – Um carro com massa inicial M0 é feito por um tubo de
área A com um comprimento horizontal L e uma altura h0. Na sua
extremidade tem uma válvula de abertura rápida e a água está
armazenada numa altura h0.
A) determine a equação para movimento do carro ao abrir a
válvula.
B) faça uma análise do movimento considerando que após os
instantes iniciais de abertura da válvula o nível de água varia
linearmente com o tempo (observação experimental)
h(t)
h0
L
V
EM 461 – Prof. Eugênio Rosa
Resposta:
A) -rALd2h/dt2 = -MdU/dt