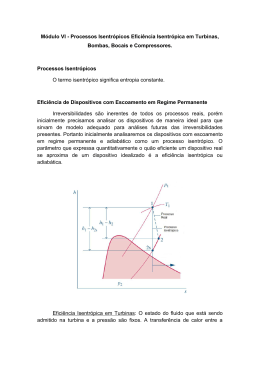
Cap. 8 – Sistemas de potência a vapor
8.1 – Modelando sistemas de potência a vapor
Central de Pego – Portugal – 584 MW
8.2 – Análise de sistemas de potência a vapor
8.2.1 – Trabalho e transferência de calor
Equação da cons. da energia :
2
2


V

V
E
S



0  Qv.c.  Wv.c.  m.(hE  hS ) 
 g( zE  zS )
2


Turbina

W
t
 h1  h2

m
expansão adiabática
Condensador:
Bomba

Q
sai
 h 2  h3

m

W
b
 h 4  h3

m
compressão adiabática
Caldeira:

Q
ent
 h1  h4

m
Eficiência ou rendimento do ciclo:

 W

W
 (h  h2 )  (h 4  h3 ) 
W
liq
t
b
 
 
 1

(
h

h
)
Q ent
Q ent
1
4


 Q

Q
(h2  h3 )
ent
sai

 1

(h1  h4 )
Qent
Razão de trabalho reversa:

W
(h4  h3 )
b
bw r   
Wt (h1  h2 )
Ciclo de Rankine ideal:
Processso 1-2 : Expansão isentrópica do fluido de trabalho => vapor saturado (1) a mistura (2)
Processso 2-3 : Rejeição de calor a pressão constante => mistura (2) a liquido saturado (3)
Processso 3-4 : Compressão isentrópica do fluido => liquido saturado (3) a líquido comprimido (4)
Processso 4-1 : Transferência de calor a pressão constante => liquido comprimido (4) a
vapor saturado (1)
Turbina a vapor multi-estágios
Exemplo 8.1 :
Calcular:
Potência líquida = 100 MW
a) Eficiência térmica:
b) razão de trabalho reversa
c) vazão de vapor em kg/h
d) taxa de transferência de calor que entra
e) taxa de transferência de calor que sai
f) vazão de água de arrefecimento (Tent = 15 oC e Tsai = 35 oC)
Ponto 1 do ciclo:
Vapor saturado a 8 MPa
tabela A-3 => h1 = 2758 kJ/kg
=> s1 = 5,7432 kJ/kg.K
Ponto 2:
1-2
Mistura líquido-vapor a 0,008 MPa
Expansão isoentrópica => s2 = 5,7432 kJ/kg.K
s2  sf 5,7432  0,5926

 0,6745
sg  s f
7,6361
Título x2
x2 
Entalpia h2
h2  hf  x2.hfg  173,88  (0,6745) 2.403,1  1.794,8 kJ / kg
Ponto 3:
líquido saturado a 0,008 MPa
Ponto 4:
líquido saturado a 8 MPa
h3 = 173,88 kJ/kg

W
h4  h3  b  h3  v 3 .(p 4  p3 )

m
h4 = 173,88+1,008x10-3 . (8-0,008)x106 / 103 kJ/kg = 173,88 + 8,06 kJ/kg
h4 = 181,94 kJ/kg
Trabalho líquido por kg de fluido
h1 = 2.758 kJ/kg


W
W
t
 b  (h1  h2 )  (h4  h3 )


m
m

W
líq
 [(2.758  1.795)  (181,9  173,9)]

m

W
líq
 963  8  955 [kJ / kg]

m
h4 = 181,9 kJ/kg
h3 = 173,9 kJ/kg
h2 = 1.795 kJ/kg
  100x1.000 [kJ / s]  1x105 [kW ]
W
líq
a)

W
 (h  h2 )  (h4  h3 ) 
955
955
   liq   1


 0,37  37%

(h1  h4 )
2
.
758

181
,
9
2
.
576
,
1
Qent 

b)

W
(h  h3 )
8
bw r   b  4

 0,0083  0,83%  1%
Wt (h1  h2 ) 963
d)
  100.000  104,7 [kg / s]  3,76x105 [kg / h]  376 [ t / h]
m
955
 m
 (h  h )  104,7 (2.758  182)  104,7 (2.576)  269,7 MW
Q
e)
 m
 (h2  h3 )  104,7 (1.795  174)  104,7 (1.621)  169,7 MW
Q
sai
c)
ent
1
4
8.2.3 – Efeitos da pressão na caldeira e no condensador
Comparação com ciclo de Carnot
8.2.4 – Irreversibilidades e perdas principais
Eficiência isentrópica da turbina
T
 m

W
h h
t
t  
 1 2
 s h1  h2s
Wt m


Eficiência isentrópica da bomba
b
s
 m


W

b
 m

W
b
s

h4s  h3
h4  h3
Exemplo 8.2 :
Calcular:
Ciclo com irreversibilidades
Eficiência da turbina e da bomba = 85%
Potência líquida = 100 MW
a) Eficiência térmica:
b) razão de trabalho reversa
c) vazão de vapor em kg/h
d) taxa de transferência de calor que entra
e) taxa de transferência de calor que sai
Ponto 1 do ciclo:
Vapor saturado a 8 MPa
tabela A-3 => h1 = 2758 kJ/kg
=> s1 = 5,7432 kJ/kg.K
Ponto 2:
1-2
Mistura líquido-vapor a 0,008 MPa
Expansão isoentrópica => s2 = 5,7432 kJ/kg.K
Entalpia h2s
Entalpia h2
h2s  hf  x2.hfg  173,88  (0,6745) 2.403,1  1.794,8 kJ / kg
h2  h1  t (h1  h2s )  2.758  (0,85)(2.758  1.794,8)  1.939 kJ / kg
h2  hf 1.939  174 1.765


 0,73
hfg
2.577  174 2.403
Título x2
x2 
Ponto 3:
líquido saturado a 0,008 MPa
Ponto 4:
h3 = 173,88 kJ/kg
líquido saturado a 8 MPa
 
W
 b   h4 s  h3  v 3 .(p 4  p3 )  8,06 [kJ / kg ]
 m

  s
 


W
W
W
8,06
b
 b   b .b 

 9,48 [kJ / kg ]
 m




m
m
0
,
85

s
h4 = 173,88+9,48 =183,36 kJ/kg
Trabalho líquido por kg de fluido


W
W
t
 b  (h1  h2 )  (h4  h3 )


m
m
h1 = 2.758 kJ/kg

W
líq
 [(2.758  1.939)  (183,4  173,9)]

m

W
líq
 819  9,5  809,5 [kJ / kg]

m
h4 = 183,4 kJ/kg
h3 = 173,9 kJ/kg
h2 = 1.939 kJ/kg
  100x1.000 [kJ / s]  1x105 [kW ]
W
líq

W
 (h  h )  (h4  h3 ) 
809,5
809,5


 0,314  31,4%
a)    liq   1 2

(h1  h4 )
2
.
758

183
,
4
2
.
574
,
6
Qent 

b)
c)
d)

W
(h  h3 ) 9,5
bw r   b  4

 0,0116  1,16%
Wt (h1  h2 ) 819
  100.000  122,1 [kg / s]  4,39x105 [kg / h]  439 [ t / h]
m
819
 m
 (h  h )  122,1(2.758  183,4)  122,1(2.574,6)  314,3 MW
Q
ent
1
4
 m
 (h2  h3 )  122,1(1.939  174)  122,1(1.765)  215,5 MW
e) Q
sai
8.3 – Superaquecimento e reaquecimento
Exemplo 8.3 :
Ciclo sem irreversibilidades
Potência líquida = 100 MW
Eficiência do ciclo = 40,3 %
  2,363x105 [kg / h]  236 [t / h]
m
Transferência de calor na caldeira = 248 MW
Transferência de calor no condensador = 148 MW
Exemplo 8.4 :
Ciclo com irreversibilidades
Eficiência isentrópica da turbina = 85%
Potência líquida = 100 MW
Eficiência do ciclo = 35,1 %
  2,782x105 [kg / h]  278 [t / h]
m
Transferência de calor na caldeira = 285 MW
Transferência de calor no condensador = 185 MW
8.4 – Ciclo de potência a vapor regenerativo
8.4.1 – Aquecedores de água abertos (misturador)
Exemplo 8.5 :
Eficiência do ciclo = 36,9 %
  3,69x105 [kg / h]  369 [t / h]
m
Ciclo com irreversibilidades
Eficiência isentrópica da turbina = 85 %
Potência líquida = 100 MW
Transferência de calor na caldeira = 271 MW
Transferência de calor no condensador = 171 MW
8.4.2 – Aquecedores de água de alimentação fechados
8.4.3 – Aquecedores de água de alimentação múltiplos
Exemplo 8.6 :
Ciclo sem irreversibilidades
Potência líquida = 100 MW
Eficiência do ciclo = 43,1 %
Sétima lista de exercícios
8.12 - 8.16 - 8.26