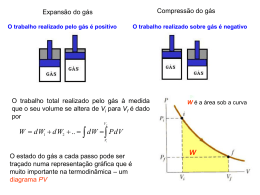
Ambiente & Energia
Ciclos Térmicos de Conversão de
Energia
Valentim M B Nunes
Unidade Departamental de Engenharias
Instituto Politécnico de Tomar, Setembro, 2014
Introdução
O desenvolvimento da máquina a vapor, uma invenção que garantiu os dois
primeiros séculos da revolução industrial, precedeu a descoberta dos princípios
científicos envolvidos, nomeadamente a produção de trabalho mecânico numa
máquina que utiliza a combustão com o ar.
O conhecimento cientifico que explica a
produção de trabalho (energia) a partir de
diferentes tipos de combustão deriva das
Leis da Termodinâmica.
James Watt (1736 – 1819)
Vamos rever como as leis da termodinâmica determinam o funcionamento
destas fontes de energia mecânica e particularmente como aquelas limitam a
quantidade de trabalho mecânico que pode ser obtido a partir da combustão de
uma dada quantidade de fuel.
Trabalho
A Termodinâmica estuda a interacção entre um dado sistema material e a sua
vizinhança ou exterior. É através destas interacções que somos capazes de
produzir trabalho mecânico ou outros efeitos úteis sobre o exterior. Existem
duas formas de interacção entre um sistema e o seu exterior, chamados
trabalho e calor. Cada um destes é um processo em que o sistema e o seu
exterior sofrem modificações químicas ou físicas relacionadas com o tipo de
interacção, calor, trabalho ou ambos simultaneamente.
Existem muitos exemplos de interacção por realização de trabalho. Considerese um gás contido num cilindro, fechado numa extremidade e equipado com
um pistão móvel.
Calor
A outra forma de interacção de um sistema com o exterior é por transferência de
calor. A uma variação de temperatura, ΔT, corresponde uma transferência de
calor Q dada por
Q  CT
em que C é a capacidade calorífica.
Usualmente designamos esta interacção por transferência de calor, embora seja
a energia que é trocada num processo deste tipo.
Lei zero da Termodinâmica
A lei zero da Termodinâmica é uma lei de equilíbrio térmico. A energia térmica
flui de uma região de alta temperatura para outra de temperatura mais baixa,
havendo uma parede diatérmica entre as duas regiões.
T/K = t/°C + 273.15
A 1ª Lei da Termodinâmica
Uma das leis fundamentais da natureza é a lei da conservação da energia. A
energia de um sistema pode assumir várias formas (por exemplo, cinética,
potencial, calor, luz), mas não pode ser criada nem destruída.
Etotal  EC  EP  U
Para sistemas fechados macroscopicamente em repouso e sem alterações do
campo gravítico
U  Q  W
A energia interna de um sistema isolado é constante. Num sistema fechado só
pode ser transferida pelo fluxo de calor ou trabalho realizado.
A 2ª Lei da Termodinâmica
Quando se projecta uma central térmica o objectivo é criar um sistema que
converta a energia de um combustível em trabalho. Se considerarmos a
combustão de um combustível fóssil, então o objectivo é converter toda a
energia do fuel em trabalho, tal como a 1ª Lei permite.
No entanto, a 2ª Lei da Termodinâmica estabelece que não é possível existir
um processo cíclico em que o calor proveniente de uma única fonte seja
inteiramente convertido em trabalho. Ao invés, apenas parte do calor pode ser
convertido em trabalho; o restante tem de ser rejeitado para um reservatório
de calor a mais baixa temperatura que a fonte de calor.
A 2ª Lei da Termodinâmica
A 2ª Lei da termodinâmica reconhece que há assimetrias fundamentais na natureza.
Por exemplo, corpos mais quentes que o ambiente arrefecem espontaneamente, mas
objectos á temperatura ambiente não se tornam espontaneamente mais quentes.
O calor transfere-se espontaneamente de corpos quentes para corpos frios.
Q
A transformação de calor em trabalho é obrigatoriamente
transferência de parte do calor para uma fonte fria.
acompanhada da
Formulações da 2ª Lei
A formulação de Kelvin da 2ª Lei afirma que não é possível haver um processo em que
o único resultado seja a absorção de calor de um reservatório e a sua conversão
completa em trabalho.
A segunda Lei diz pois que a transformação de
calor
em
trabalho
é
obrigatoriamente
acompanhada pela transferência de parte do calor
para uma fonte fria. Mais uma assimetria da
Natureza: é impossível converter calor totalmente
em trabalho, mas não há restrição na conversão de
trabalho em calor.
Combustão de combustíveis fósseis
A fonte de energia que é utilizada nos sistemas de combustão de combustíveis
fósseis é a energia química que é libertada quando o fuel é oxidado por queima
com o ar. Os combustíveis fósseis mais comuns são hidrocarbonetos, misturas
de moléculas compostas por carbono e hidrogénio. Após a combustão
completa, o fuel é oxidado a dióxido de carbono e vapor de água, libertando
energia.
Designando as moléculas de combustível por CnHm, onde n e m são o
número de átomos de carbono e hidrogénio na molécula de fuel, o rearranjo
molecular que acompanha a oxidação completa pode ser representado pela
reacção:
Poder calorífico dos combustíveis
Quando uma mistura de fuel e ar é queimada, a temperatura dos produtos de
combustão formados é muito maior que a da mistura. Em muitos casos, o calor
pode ser transferido dos produtos de combustão quentes para um fluido mais
frio; por exemplo, num vaporizador o calor aquece água e depois leva-a à
ebulição convertendo-a em vapor de água. A quantidade de calor disponível
para este processo é designado poder calorífico do combustível (fuel heating
value) e é normalmente expresso em unidades de energia por unidade de
massa do combustível.
Ciclos térmicos ideais
Para compreender as implicações das leis da Termodinâmica para a
conversão da energia dos combustíveis em trabalho mecânico, é conveniente
analisar dispositivos ideais, nos quais um fluido é aquecido e arrefecido e
produz ou consome trabalho, à medida que completa um ciclo. Um dispositivo
deste tipo pode ser chamado uma máquina térmica, uma vez que troca calor
com o seu exterior enquanto produz trabalho num processo cíclico. A
combustão do fuel é representada neste ciclo ideal pela adição de calor a
partir de uma fonte quente. Algumas máquinas práticas, como a turbina a gás
e os motores automóveis, não são aquecidos por uma fonte externa. Estes são
designados motores de combustão interna. No entanto muito do seu
funcionamento pode ser modelado como máquinas térmicas ideais para
compreendermos o seu funcionamento.
Eficiência termodinâmica
Particularmente importante é a quantidade de trabalho produzida (W) em
relação à quantidade de calor adicionado (Q) para representar a combustão
do fuel. A esta razão chamamos eficiência termodinâmica:
w

Q
O ciclo de Carnot
O ciclo de Carnot é o protótipo de um ciclo que tem pouca importância prática
mas é elegantemente ilustrativo das limitações da 2ª Lei na conversão de calor
em trabalho. Trata-se do mais simples ciclo de uma máquina térmica. Consiste
de dois reservatórios térmicos , um reservatório quente à temperatura Th e um
reservatório frio à temperatura Tc. (podemos imaginar a fonte quente mantida a
essa temperatura por transferência de calor a partir da queima de um
combustível fóssil e a fria como a atmosfera)
Considere-se então a máquina térmica como sendo um cilindro equipado com
um pistão móvel e contendo um fluido de massa unitária. O ciclo consiste em
quatro passos: uma expansão isotérmica, durante a qual uma quantidade de
calor Qh é adicionada à máquina (1 → 2 na Figura); uma expansão adiabática
isentrópica durante a qual a temperatura do fluido decresce de Th para Tc (2 →
3); uma compressão isotérmica enquanto o sistema transfere uma quantidade
de calor Qc para o reservatório frio (3 → 4); e finalmente um compressão
isentrópica para o estado inicial(4 → 1). Para este ciclo o trabalho do pistão
por ciclo é:
Combinando as duas relações anteriores podemos calcular a eficiência
termodinâmica do ciclo de Carnot:
O aspecto mais importante deste resultado é que a eficiência termodinâmica
depende das temperaturas dos dois reservatórios e não depende de todo de
qualquer das propriedades do fluido utilizado na máquina térmica.
Princípios de Carnot
A segunda Lei impõe limites ao funcionamento de dispositivos cíclicos: Uma máquina
térmica não pode funcionar através da troca de calor com uma única fonte!
Podemos retirar duas conclusões (princípios de Carnot)
1. O rendimento de uma máquina térmica irreversível é sempre inferior ao de uma
máquina térmica reversível que funciona entre as mesmas fontes (temperaturas)
2. Os rendimentos de todas as máquinas térmicas reversíveis que funcionam entre as
mesmas duas fontes são iguais.
O rendimento máximo de uma central térmica a vapor
que funcione entre TH = 750 K e TC = 300 K é de 60 %. A
eficácia térmica real ronda os 38 – 40%.
O ciclo de Rankine
O ciclo de Carnot é um processo importante para compreendermos como
funciona uma máquina térmica simples, mas não é util em termos práticos.
Desde o início da revolução industrial até ao séc XX (e ainda actualmente), a
maior parte da potência mecânica gerada pela queima de combustíveis
fósseis utiliza um ciclo a vapor, chamado ciclo de Rankine. Numa central
térmica com ciclo de vapor, o combustível misturado com o ar é queimado
para num vaporizador converter água em vapor, que depois alimenta uma
turbina. Este é um sistema de combustão externa onde o fluido de trabalho,
água-vapor, é aquecido em tubos que estão em contacto com os gases
quentes formados na câmara de combustão. Numa central térmica eficiente,
praticamente todo o valor calorífico do fuel é transferido para o vaporizador,
mas apenas uma parte é convertida em trabalho na turbina.
Ciclo de Rankine
Esquema de Central Termoelétrica
de Produção de Energia
Numa central térmica a vapor, água à temperatura ambiente é bombeada a alta
pressão e injectada no vaporizador (1 → 2 na Figura), sendo aquecida até ao
seu ponto de ebulição(3), completamente convertida em vapor(4), e depois
normalmente aquecida até uma temperatura mais elevada(5). Este aquecimento
no vaporizador ocorre a pressão constante, pb. A corrente de vapor flui através
de uma turbina (5 → 6) onde sofre uma redução de pressão para um valor muito
mais baixo, pc, enquanto a turbina produz potencia motor. O vapor a baixa
pressão que deixa a turbina é arrefecido a um liquido à temperatura ambiente
no condensador (6 → 1) e bombeada para o vaporizador onde completa o ciclo.
No ciclo ideal de Rankine, o trabalho adiabático em fluxo contínuo por unidade de
massa de vapor, wt produzido na turbina é igual à variação de entalpia h5 − h6
através da turbina, em virtude da primeira lei. Como se trata de um processo
isentrópico, a variação de entalpia pode ser expressa através de:
Existe uma expressão similar para calcular o trabalho necessário para operar a
bomba. O trabalho total w produzido no ciclo pode ser expresso por:
onde vs e vw são os volumes específicos do vapor na turbina e da água na
bomba e pb e pc são as pressões no vaporizador e no condensador. Uma vez
que o volume específico da água liquida é muitíssimo menor que o do vapor, a
potência da bomba é uma pequena fracção da potencia produzida na turbina, o
que é um dos grandes atributos do ciclo de Rankine. Uma vez que os passos de
aquecimento e arrefecimento do ciclo ideal de Rankine (2 → 5, 6 → 1) ocorrem
a pressão constante, enquanto o passo na turbina é isentrópico a eficiência
térmica pode ser expressa por:
Convém realçar alguns aspectos relativos ao ciclo de Rankine. Primeiro, ao
contrário do ciclo de Carnot, a eficiência térmica depende das propriedades do
fluido de trabalho, a água. Segundo, a eficiência do ciclo aumenta se a pressão
no vaporizador (e temperatura do vapor) aumentarem. Ao mesmo tempo,
elevadas pressões no vaporizador aumentam a quantidade de trabalho
produzida por unidade de massa de água fluindo no sistema, e reduzindo os
custos da turbina por unidade de potencia produzida. O ciclo pode ainda ser
melhorado com ganhos de eficiência pela utilização de permutadores de calor
as níveis de pressão intermédios.
Para os ciclos de Rankine que usam água como fluido de trabalho as
temperaturas do vaporizador raramente excedem os 550 ◦C. Um ciclo de mais
alta pressão e mais altas temperaturas é aquele para o qual a pressão e
temperatura do vapor excedem o ponto crítico da água.
A eficiência termodinâmica do ciclo ideal de Rankine varia no intervalo de 30 a
45%, dependendo dos detalhes e complexidade do ciclo. As actuais centrais a
ciclo de vapor têm eficiências mais baixas por vários motivos. As turbinas e
bombas não são 100% eficientes, resultando em menos potencia produzida.
Ciclo de Otto
O mais comum dos motores movidos a combustíveis fósseis é o motor
automóvel. Ao contrário das centrais a vapor, os motores automóveis não
dependem da transferência de calor de um fluido de trabalho a partir de uma
fonte de combustão. Em vez disso, o fuel é queimado adiabaticamente
dentro do motor, e os produtos de combustão produzem mais trabalho
durante o passo de expansão, do que aquele que é utilizado no passo de
compressão. Os produtos de combustão que são despejados na atmosfera
são substituídos por uma mistura de ar-fuel para dar inicio ao novo ciclo. Isto
é designado por ciclo aberto, ao contrário do ciclo a vapor que é fechado.
Ciclo de Otto
O ciclo de Otto é o ciclo ideal para motores a gasolina. Na maior parte dos motores a
gasolina o êmbolo realiza quatro cursos completos no interior do cilindro. A cambota
realiza duas rotações completas por cada ciclo termodinâmico.
1-2: Compressão adiabática; 2-3:Adição de calor a volume constante
3-4: Expansão adiabática; 4-1: rejeição de calor a volume constante.
A eficiência do ciclo de Otto aumenta em função da razão de compressão,
ve/vc, e depende das propriedades termodinâmicas do fluido de trabalho. Pode
ser expressa por:
Para um motor a gasolina típico o ratio de compressão é cerca de 9 e cp/cv =
1.26, logo η = 43.5%.
As eficiências dos motores automóveis são bastante menores que aquele valor.
A fricção nos pistões, potencia necessária para operar as válvulas, bomba de
arrefecimento, sistema de fornecimento do combustível, perdas de pressão nos
sistemas de admissão e exaustão e perdas de calor durante os passos de
compressão e expansão, tudo contribui para reduzir a eficiência. As melhores
eficiências térmicas de motores automóveis variam entre 28% e 39% para os
motores a gasolina e a diesel.
Ciclo de Brayton
Desde meados do séc XX, a turbina a gás tornou-se a tecnologia dominante
para motores de grandes aeronaves, por causa da sua adequação a altas
velocidades de propulsão, leveza, economia de combustível e fiabilidade.
Também tem aplicação em propulsão de grandes navios e mais recentemente
em centrais térmica de produção de electricidade.
O ciclo ideal que modela o processo de combustão do gás através de uma
central a turbina de gás é o ciclo de Brayton. Consiste numa compressão
isentrópica do ar num compressor à pressão de entrada pi para a pressão de
saída do compressor, pc (1 → 2 na Figura), seguido de um aquecimento a
pressão constante (2 → 3) que sobe a temperatura do gás para a temperatura
T3 à entrada da turbina. Os gases expandem isentropicamente enquanto
fluem através da turbina, sendo a pressão reduzida de pc para pi (3 → 4).
Por unidade de massa do fluido, o trabalho resultante , w, na central a turbina
de gás é a diferença entre o trabalho na turbina e o trabalho no compressor:
O calor adicionado ao fluido proveniente do compressor , q, que é devido à
subida de temperatura causada pela combustão adiabática, é igual à variação
de entalpia no processo a pressão constante:
Assim, a eficiência η do ciclo de Brayton é:
A eficiência do ciclo depende da razão entre as duas pressões p2/p1 = p3/p4
e das propriedades termodinâmicas do ar e dos gases de combustão. Esta
eficiência é expressa por:
O que mostra que a eficiência aumenta com a razão de compressão. Como
exemplo p2/p1 = 10 e cp/cv = 1.3, então η = 41.2%. Para o ciclo de Brayton as
melhores eficiências rondam os 33%.
Ciclo combinado
Os gases de combustão que saem de uma turbina a gás transportam parte
do pode calorífico do fuel que não foi convertido em trabalho. Esta corrente
gasosa quente pode ser utilizada para produzir vapor num vaporizador e
produzir trabalho adicional sem queimar mais combustível. A utilização de
uma turbina a gás e central a vapor para produzir mais trabalho a partir de
uma dada quantidade de fuel é chamado ciclo combinado.
A eficiência termodinâmica, ηcc de uma central térmica de ciclo combinado pode
ser determinada em função das eficiências , ηg e ηs , da turbina a gás e do ciclo
de vapor. Para a turbina a gás, o trabalho wg é igual a ηg × qf , onde qf é o calor
adicionado por unidade de massa dos produtos de combustão. A quantidade de
calor que pode ser utilizada no ciclo a vapor é qf −wg = qf (1−ηg). O trabalho
produzido no ciclo a vapor ws é então ηs vezes este calor, ou ηs qf (1 − ηg).
A eficiência do ciclo combinado é sempre inferior à soma das eficiências dos
dois ciclos (Brayton e Rankine). No entanto a combinação é sempre mais
eficiente que qualquer um dos componentes. Por exemplo se ηg = 30% e ηs =
25%, então ηcc = 47.8%.
As centrais térmica de ciclo combinado que queimam gás natural ou jet fuel
são muitas vezes uma boa escolha, em vez de centrais térmicas a carvão,
apesar do preço favorável do carvão. As razões são financeiras e
ambientais, incluindo uma menor emissão de poluentes gasosos, incluindo
o CO2.
Problema
1
São necessários 2.2 milhões de toneladas de carvão por ano para alimentar
uma central termoeléctrica de 1000-MW que opera com um factor de
capacidade de 70%. Se o poder calorífico do carvão for 12 000 Btu/lb,
calcular a eficiência térmica da central.
Problema
2
Dada uma razão de compressão p2/p1 = 12 ao longo de uma turbina a gás e
uma razão entre calores específicos de cp/cv = 1.35 relativos ao fluido de
trabalho, calcular a eficiência térmica do ciclo de Brayton. Explicar porque
motivo a centrais com turbina a gás atingem eficiências térmicas de apenas
25% a 35%.
Problema 3
Uma central termoeléctrica de ciclo combinado possui uma turbina a gás com
eficiência de 30% e um ciclo a vapor com eficiência de 30%. Calcular a
eficiência do ciclo combinado.
Problema 4
Uma central termoeléctrica de 1000-MW com uma eficiência térmica de 35%,
durante 100% do tempo, usa carvão com a fórmula CH e um poder calorífico
de 30 MJ/kg. Quanto CO2 emite esta unidade em toneladas/ano?
Bibliografia
Fay, J., Golomb, D.S., Energy and the Environment, Oxford University Press
and Open University, Oxford, UK, 2004
Azevedo, E.G., Termodinâmica Aplicada, 3ºed., Escolar Editora, Lisboa, 2011