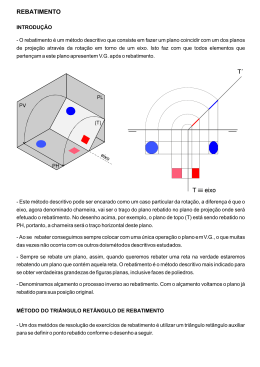
GEOMETRIA DESCRITIVA A
11.º Ano
Axonometrias Ortogonais - Dimetria
© antónio de campos, 2010
PERSPECTIVA DIMÉTRICA
Se dois dos três ângulos do triedro com o plano axonométrico forem iguais, será uma
perspectiva dimétrica, com o triângulo fundamental a ser um triângulo isósceles.
Os ângulos serão sempre ângulos obtusos.
A pirâmide axonométrica é uma pirâmide recta, mas não regular.
z
z
y
x
zp
αº
βº
αº
O
βº
α
yp
O ≡ Op
y
αº
xp
αº
x
REBATIMENTO DOS PLANOS PROJECTANTES DOS EIXOS
Através do processo de rebatimento dos planos projectantes dos eixos, é possível obter
graficamente o coeficiente de redução, sem recorrer a tabelas e a cálculos matemáticos.
Tal como a perspectiva isométrica, é possível obter os coeficientes de redução sem rebater
todos os três planos projectantes dos eixos, mas no caso da perspectiva dimétrica, através
de dois rebatimentos de um plano projectante de um eixo.
z
Para uma perspectiva dimétrica de um ponto P (3;
4; 5); com a perspectiva do eixo z a fazer um
ângulo de 110º com a perspectiva do eixo x, e a
perspectiva do eixo y a ter um coeficiente de
redução isolado.
C
pr
Começa-se pela representação de um triângulo
fundamental [ABC], que é um triângulo isósceles.
Or
Para determinar a abcissa do ponto P, é
necessário rebater o plano projectante do eixo x,
com o eixo x como charneira.
Q é o ponto de intersecção da charneira com o
segmento [BC].
[AQ] é a hipotenusa do triângulo [AOQ].
pr é a recta projectante do ponto O em
rebatimento.
O triângulo [AOrQ] é o triângulo [AOQ] em
rebatimento.
ir é a recta de intersecção do plano projectante
do eixo x (plano π) com o plano yz.
O segmento [OrRr] representa a V.G. de abcissa.
A seguir é possível obter a cota, utilizando o eixo
xr, pois os eixos x e z têm o mesmo coeficiente
x
de redução.
Já para o afastamento será necessário rebater o
eixo y.
i’r
Q’
p’r
R’
O’r
P2
P3
Rr
P
Q
R’r
O
R’’r
R
ir
R’’
A
P1
B
xr
yr
y
Considera uma
perspectiva
dimétrica, em
que a perspectiva
do eixo x faz um
ângulo de 130º
com a
perspectiva do
eixo z, e a
perspectiva do
eixo y a ter um
coeficiente de
redução isolado.
z
zr
Or
S2
R3
S3 ≡ S
R2 ≡ R
Desenha a
perspectiva do
triângulo [RST],
via o
rebatimento dos
planos
projectantes do
eixo, sendo R (4;
0; 5), S (0; 2; 6)
e T (2; 5; 2).
T2
O
O’r
S1
R1
T3
T
T1
y
yr
x
REBATIMENTO DOS
PLANOS COORDENADOS –
Definidos por um par de
eixos
z’r
Através do processo de rebatimento
dos planos coordenados, é possível
obter graficamente o coeficiente de
redução, sem recorrer a tabelas e a
cálculos matemáticos.
Or
z
Para uma perspectiva dimétrica de
um ponto P (3; 4; 5); com a
perspectiva do eixo z a fazer um
ângulo de 110º com a perspectiva do
eixo x, e a perspectiva do eixo y a
ter um coeficiente de redução
isolado.
P2
zr
O’r
P3
P
Começa-se pela representação
de um triângulo fundamental.
O
O rebatimento do plano xz
rebate dois eixos.
O rebatimento do plano xy
rebate o outro eixo.
P1
x
xr
yr
y
É dado um prisma
quadrangular regular, com
7 cm de altura, situado no
1.º tiedro.
z
A base inferior do prisma é
o quadrado [ABCD] e a
base superior o quadrado
[A’B’C’D’]. As bases estão
contidas em planos
fν
horizontais.
A (1; 5; 0) e C (7; 5; 0)
são dois vértices opostos
do quadrado [ABCD], sendo
D o vértice de maior
afastamento do quadrado.
B’3
A’2
B’2 ≡ D’2
A’1 ≡ A’
B’1 ≡ B’
C’2
D’3
pν
D’1 ≡ D’
C’1 ≡ C’
A2
xr
O
B3
B2 ≡ D2
C2
C1 ≡ C
Or
A3≡ C3
A1 ≡ A
B1 ≡ B
Considera que a
perspectiva do eixo x faz
ângulos de 130º com as x
perspectivas dos outros
dois eixos.
Desenha a perspectiva
dimétrica do prisma, via o
rebatimento dos planos
coordenados.
A’3 ≡ C’3
D1 ≡ D
D3
yr
y
MÉTODO DOS CORTES
Semelhante ao processo de rebatimento dos planos coordenados, é outro método para obter
graficamente o coeficiente de redução, sem recorrer a tabelas e a cálculos matemáticos. A
diferença entre os dois métodos é que neste método dos cortes, o rebatimento dos planos
coordenados se processa para o interior da pirâmide axonométrica.
zr
z
zr
Para uma perspectiva
dimétrica de um ponto P
(3; 4; 5); com a perspectiva
do eixo z a fazer um ângulo
de 110º com a perspectiva
do eixo x, e a perspectiva
do eixo y a ter um
coeficiente de redução
isolado.
P2
Começa-se pela
representação de um
triângulo fundamental.
P3
P
O rebatimento do plano
xz rebate dois eixos.
O
O’r
O rebatimento do plano
xy rebate o outro eixo.
Or
P1
xr
x
yr
y
PERSPECTIVA DIMÉTRICA NORMALIZADA
Numa perspectiva dimétrica, a perspectiva de um dos eixos faz ângulos de 131º 30’
(arredondado de 131º 24’) com as perspectivas dos outros dois eixos, que, por sua vez, fazem
entre si um ângulo de 97º (arredondado de 97º 11’).
O coeficiente de redução é de 0,5 (arredondado de 0,47) para o eixo com uma redução
perspectiva isolada, e de 1 (arredondado de 0,94) para para os outros dois eixos.
Para uma perspectiva dimétrica
normalizada de um ponto P (3; 4;
5), com a perspectiva do eixo y a
ter um coeficiente de redução
isolado.
z
P2
P3
P
O
x
P1
y
2
Considera que a perspectiva do
eixo x tem um coeficiente de
redução isolado.
3
1
3
4
A2
Desenha a perspectiva dimétrica
normalizada do objecto.
3
A3
3
2
2
A1
2
z
O
A2
A3
A1≡ A
x
1
1
As dimensões apresentadas são
em centímetros, e as coordenadas
de A (2; 2; 0).
y
1
z
É dada uma pirâmide
pentagonal regular,
com 8 cm de altura.
O’r
A base está contida
num plano horizontal,
cujo centro é o ponto
Q (4; 5; 2), com o
lado de menor
afastamento frontohorizontal.
V3
zr
OV
E
Desenha a
perspectiva
dimétrica da
pirâmide.
Q3
B3 ≡ D3
O pentágono da base
inscreve-se numa
circunferência com
3,5 cm de raio.
xr
Considera que a
perspectiva do eixo z
faz ângulos de 130º
com as perspectivas
dos outros dois
eixos.
A3 ≡ E3
D
C3
A
Q
B1r
fν
yr
C1r
C
B
x
pν
Q1r ≡ V1r
A1r
D1r
E1r
Or
y