Capítulo 3
3. Materiais cristalinos
-Estrutura cristalina: Conceitos Fundamentais,
célula unitária,
- Sistemas cristalinos,
- Polimorfismo e alotropia
- Direções e planos cristalográficos, anisotropia,
- Determinação das estruturas cristalinas por
difração de raios-x.
1
Capítulo 3
A estrutura de sólidos cristalinos
Por que estudar a estrutura de sólidos cristalinos?
 As propriedades de alguns materiais estão diretamente relacionadas às suas
estruturas cristalinas.
ex: Magnésio e Berílio que têm a mesma estrutura se deformam muito
menos que ouro e prata que têm outra estrutura cristalina.
 Explica as diferenças significativas nas propriedades apresentadas por materiais
cristalinos e não-cristalinos que possuem a mesma composição.
Exemplo: cerâmicas e polímeros não cristalinos são normalmente
opticamente transparentes; os mesmos materiais em forma cristalina
tendem a ser opaco ou, na melhor das hipóteses, translúcidos.
2
ESTRUTURAS CRISTALINAS(CONT.)
• Os
materiais
sólidos
podem
ser
classificados em cristalinos ou nãocristalinos de acordo com a regularidade
na qual os átomos ou íons se dispõem em
relação à seus vizinhos.
• Material cristalino é aquele no qual os
átomos encontram-se ordenados sobre
longas distâncias atômicas formando uma
estrutura tridimensional que se chama de
rede cristalina
• Todos os metais, muitas cerâmicas e alguns
polímeros formam estruturas cristalinas sob
condições normais de solidificação
3
O Cristal Perfeito - Estrutura Cristalina
 Muitos materiais - metais, algumas cerâmicas, alguns
polímeros - ao se solidificarem, se organizam numa rede
geométrica 3D - a rede cristalina.
Estes materiais cristalinos, têm uma estrutura altamente
organizada, em contraposição aos materiais amorfos, nos quais
não há ordem de longo alcance.
Cristal 1
Fronteira
Cristal 2
Fronteira entre dois cristais de TiO2.
Carbono amorfo.
Note a organização geométrica dos átomos. Note a desorganização na posição dos átomos.
Imagens obtidas com Microscópio Eletrônico de Transmissão (MET).
4
Nos Materiais Não-Cristalinos ou Amorfos não existe ordem de longo
alcance na disposição dos átomos
Ordenamento regular dos átomos
Ordenamento somente a curtas distâncias
As propriedades dos materiais sólidos cristalinos depende da estrutura
cristalina, ou seja, da maneira na qual os átomos, moléculas ou íons estão
espacialmente dispostos.
Há um número grande de diferentes estruturas cristalinas, desde
estruturas simples exibidas pelos metais até estruturas mais complexas
exibidas pelos cerâmicos e polímeros
5
Célula Unitária
(unidade básica repetitiva da estrutura tridimensional)
Como a rede cristalina tem uma estrutura repetitiva, é
possível descrevê-la a partir de uma estrutura básica,
como um “tijolo”, que é repetida por todo o espaço.
Células Não-Unitárias
Célula Unitária
Menor “tijolo” que repetido
reproduz a rede cristalina
6
CÉLULA UNITÁRIA(CONT.)
(unidade básica repetitiva da estrutura tridimensional)
Consiste num pequeno grupos de átomos que formam um modelo
repetitivo ao longo da estrutura tridimensional (analogia com elos da
corrente)
A célula unitária é escolhida para representar a simetria da estrutura
cristalina
Os átomos são representados como esferas rígidas
7
Sistemas Cristalinos
Estes sistemas incluem tôdas as possíveis geometrias de
divisão do espaço por superfícies planas contínuas
Reticulado
x, y, z = eixos
a, b, c = comprimentos das
arestas
, ,  = ângulos interaxiais
Célula Unitária
Os 7 Sistemas Cristalinos
 Só existem 7 tipos de células unitárias que preenchem
totalmente o espaço
Cúbica
a=b=c, °
Hexagonal*
Romboédrica
a=b=c, ° a=bc, °°
Tetragonal
a=bc, °
Monoclínica
abc, ° 
Ortorrômbica
abc, °
Triclínica
abc, °
9
Sistemas Cristalinos e Redes de Bravais
 Os sistemas cristalinos são apenas entidades geométricas.
Quando posicionamos átomos dentro destes sistemas formamos
redes (ou estruturas) cristalinas.
 Existem apenas 14 redes que permitem preencher o espaço 3D.
 Nós vamos estudar apenas as redes mais simples:
a cúbica simples - cs (sc - simple cubic)
 a cúbica de corpo centrado - ccc (bcc - body centered cubic)
 a cúbica de face centrada - cfc (fcc - face centered cubic)
 a hexagonal compacta - hc (hcp - hexagonal close packed)
10
AS 14 REDES DE BRAVAIS
Dos 7 sistemas cristalinos podemos identificar 14 tipos
diferentes de células unitárias, conhecidas com redes de
Bravais. Cada uma destas células unitárias tem certas
características que ajudam a diferenciá-las das outras
células unitárias. Além do mais, estas características
também auxiliam na definição das propriedades de um
material particular.
As 14 Redes de Bravais
Cúbica Simples Cúbica de Corpo
Centrado
Ortorrrômbica
Simples
Hexagonal
Cúbica de Face
Centrada
Ortorrrômbica de
Corpo Centrado
Monoclínica
Simples
Ortorrrômbica de
Base Centrada
Tetragonal
Simples
Tetragonal de
Corpo Centrado
Ortorrrômbica de
Face Centrada
Monoclínica de
Base Centrada
Romboédrica
Simples
Triclínica
12
POLIMORFISMO OU ALOTROPIA
•Alguns metais e não-metais podem ter mais de uma
estrutura cristalina dependendo da temperatura e
pressão. Esse fenômeno é conhecido como
polimorfismo.
• Geralmente as transformações polimorficas são
acompanhadas de mudanças na densidade e
mudanças de outras propriedades físicas.
EXEMPLO DE MATERIAIS QUE
EXIBEM POLIMORFISMO
•
•
•
•
•
Ferro
Titânio
Carbono (grafite e diamente)
SiC (chega ter 20 modificações cristalinas)
Etc.
ALOTROPIA DO FERRO
ccc De 1394°C-PF
cfc
De 910-1394°C
ccc
Até 910°C
• Na temperatura ambiente, o
Ferro têm estrutura ccc, número
de coordenação 8, fator de
empacotamento de 0,68 e um
raio atômico de 1,241Å.
• A 910°C, o Ferro passa para
estrutura cfc, número de
coordenação 12, fator de
empacotamento de 0,74 e um
raio atômico de 1,292Å.
• A 1394°C o ferro passa
novamente para ccc.
Estruturas Cristalinas dos Metais
 Como a ligação metálica é não direcional não há grandes
restrições quanto ao número e posição de átomos vizinhos.
Assim, os metais terão NC alto e empilhamento compacto.
 A maior parte dos metais se estrutura nas redes cfc, ccc e hc
 Daqui prá frente representaremos os átomos como esferas
rígidas que se tocam. As esferas estarão centradas nos pontos
da rede cristalina.
16
A rede ccc
 A rede cúbica de corpo centrado é uma rede cúbica na qual
existe um átomo em cada vértice e um átomo no centro do
cubo. Os átomos se tocam ao longo da diagonal.
Fator de empacotamento atômico
(APF - atomic packing factor)
Volum e(átom os)

a
Volum e(célula)
N (átom os)V (1átom o)
R


3
a
4 3
N (átom os) R
1 átomo inteiro
1/8 de átomo
3

a3
Número de átomos na célula unitária
4
8 3
Na= 1 + 8x(1/8) = 2
2  R 3
R
3
Relação entre a e r
3
3
FEAccc 


  0,68
3
3
4R = a3 => a = 4R/3
NC = 8
64R
8
 4R 


17
3
3
O Fe, Cr, W cristalizam em ccc
3


FEA 
Estrutura Cristalina Cúbica de Corpo Centrado (CCC)

2 átomos/c.u.

N.C. = 8

F.E.A. = 0.68

Cr, Fe(a), W
18
A rede cfc
 A rede cúbica de face centrada é uma rede cúbica na qual existe
um átomo em cada vértice e um átomo no centro de cada face
do cubo. Os átomos se tocam ao longo das diagonais das faces
do cubo.
Al, Ag, Cu, Au
a
1/8 de átomo
R
1/2 átomo
Número de átomos na célula unitária
Na= 6x1/2 + 8x(1/8) = 4
Relação entre a e r
4R = a2 => a = 2R2
NC = 12
Fator de empacotamento atômico
FEAcfc = Volume dos átomos = 0.74
Volume da célula
A rede cfc é a mais compacta
19
Estrutura Cristalina Cúbica de Face Centrada (CFC)
a = parâmetro de rede
R = raio atômico

4 átomos/c.u.

N. C. = 12

F.E. A. = 0.74

Al, Cu, Au, Pb, Ni, Pt, Ag
20
EST. HEXAGONAL COMPACTA
• Cada átomo tangencia 3
átomos da camada de cima,
6 átomos no seu próprio
plano e 3 na camada de
baixo do seu plano
• O número de coordenação
para a estrutura HC é 12 e,
portanto, o fator de
empacotamento é o mesmo
da cfc, ou seja, 0,74.
a = parâmetro de rede
R = raio atômico
Relação entre R e a:
a= 2R
A rede hc
 A rede hexagonal compacta pode ser representada por um
prisma com base hexagonal, com átomos na base e topo e um
plano de átomos no meio da altura.
Cd, Mg, Ti, Zn
Número de átomos na célula
unitária
Na= 12x1/6 + 2x(1/2) + 3 = 6
Relação entre a e r
2R = a
c
c/2
FEA = 0.74
NC =12
A rede hc é tão compacta quanto
a cfc
a
22
A rede hc (cont.)
Cálculo da razão c/a
Vista de topo
a/2
30º
d
dcos30° = a/2
d3/2 = a/2
d = a/3
a
c/2
a
a
d
a2 = a2/3 +c 2/4  c2 = 8a2/3
a
a2 = d2 +(c/2)2
Razão c/a ideal
c/a= 8/3 = 1.633
no entanto este valor varia em metais reais
23
A rede hc (cont.)
 Cálculo do fator de empacotamento atômico
FEA 
Vatomos
Vcelula
4
Vatomos  6  r 3  8r 3
3
Vcelula  Abase  Altura  Ahexagono  c  6  Atriang.  c
3
a
b h
2  a2 3
Atriang. 

2
2
4
3
3 8
Vcelula  6  a 2
 c  6  a2

a  3 2a 3  3 2 8r 3
4
4
3
Vista de topo
a
FEA 
3
8r


 0.74
3
3 2
3 2 8r
h
60º
a
24
Empacotamento ótimo
 O fator de empacotamento de 0.74, obtido nas redes cfc e hc, é
o maior possível para empilhar esferas em 3D.
A
A
B
C
A
A
C
B
C
A
B
cfc
A
B
C
A
C
C
A
B
C
A
B
A
B
B
C
A
B
C
A
B
C
A
C
A
B
A
A
A
B
C
A
A
hc
25
Empilhamento de planos compactos das estruturas CFC e HC
26
Cristalografia
• Para poder descrever a estrutura cristalina é necessário
escolher uma notação para posições, direções e planos.
• Posições
 São definidas dentro de um cubo com lado unitário.
27
Direções Cristalográficas e Pontos do Retículo
• Vetores
vetor decomposição
•Direção Cristalográfica
Um vetor se posiciona de tal modo que ele passe pela origem do sistemas de
coordenadas;
O comprimento da projeção do vetor em cada um dos 3 eixos é determinado;
Estes 3 números são reduzidos ao menor número inteiro;
Eles são representados dentro de colchetes, [uvw]
Índices de uma direção [120]
x
y
z
Projeções
a/2
b
0c
Projeções
1/2
1
0
Reduções
1
2
0
Representação [120]
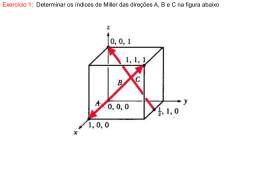
Direções cristalográficas
 As direções são definidas a partir da origem.
 Suas coordenadas são dadas pelos pontos que cruzam o cubo
unitário. Se estes pontos forem fraccionais multiplica-se para
obter números inteiros.
[0 0 1]
[1 1 1]
[1 -1 1]
1 1 1
[0 1 1/2]=[0 2 1]
[0 1 0]
[1/2 1 0]=[1 2 0]
[1 0 0]
[1 1 0]
29
Direções cristalográficas (cont.)
• Famílias de direções
 Formadas por posições semelhantes dentro da estrutura
cristalina.
<111> = [111],[111],[111],[111],[111],[111],[111],[111]
• Ângulo entre direções no sistema cúbico
 Dado pelo produto escalar entre as direções, tratadas como
vetores.
D=ua +vb + wc
D’=u’a +v’b + w’c
Ex: [100] e [010]
cos= 1.0 + 0.1 + 0.0 = 0
D.D’ = /D/ /D’/ cos 
1
= 90°
cos  = D.D’/ /D/ /D’/ = uu’+vv’+ww’/ u2+v2+w2 u’2+v’2+w’2
Ex: [111] e [210]
cos= 1.2 + 1.1 + 1.0 = 3
3.5
5
= 39.2°
30
DIREÇÕES NOS CRISTAIS
• São representadas
entre colchetes=[uvw]
• Família de direções:
<uvw>
Algumas direções da
família de direções <100>
DIREÇÕES NOS CRISTAIS
• São representadas entre
colchetes= [hkl]
• Se a subtração der
negativa, coloca-se uma
barra sobre o número
As duas direções
pertencem a mesma
família?
[101]
DIREÇÕES NOS CRISTAIS
• São representadas entre
colchetes= [hkl]
• Quando passa pela
origem
DIREÇÕES NOS CRISTAIS
• São representadas entre
colchetes= [hkl]
Os números devem ser divididos
ou multiplicados por um
fator comum para dar números
inteiros
DIREÇÕES PARA O
SISTEMA CÚBICO
A simetria desta estrutura permite que as direções equivalentes sejam
agrupadas para formar uma família de direções:
• <100> para as faces
• <110> para as diagonais das faces
• <111> para a diagonal do cubo
<110>
<111>
<100>
DIREÇÕES PARA O
SISTEMA CCC
• No sistema ccc os átomos se
tocam ao longo da diagonal
do cubo, que corresponde a
família de direções <111>
• Então, a direção <111> é a
de maior empacotamento
atômico para o sistema ccc
DIREÇÕES PARA O
SISTEMA CFC
• No sistema cfc os átomos
se tocam ao longo da
diagonal da face, que
corresponde a família de
direções <110>
• Então, a direção <110> é a
de maior empacotamento
atômico para o sistema cfc
PLANOS CRISTALINOS
Por quê são importantes?
· Para a determinação da estrutura cristalina Os métodos de
difração medem diretamente a distância entre planos paralelos de
pontos do reticulado cristalino. Esta informação é usada para
determinar os parâmetros do reticulado de um cristal.
Os métodos de difração também medem os ângulos entre os planos
do reticulado. Estes são usados para determinar os ângulos
interaxiais de um cristal.
· Para a deformação plástica
A deformação plástica (permanente) dos metais ocorre pelo
deslizamento dos átomos, escorregando uns sobre os outros no cristal.
Este deslizamento tende a acontecer preferencialmente ao longo de
planos direções específicos do cristal.
Planos cristalográficos
• A notação para os planos utiliza os índices de Miller,
que são obtidos da seguinte maneira:
 Obtém-se as intersecções do plano com os eixos.
 Obtém-se o inverso das intersecções.
 Multiplica-se para obter os menores números inteiros.
1
Intersecções: 1/2, 1
Inversos: 2, 0 ,1
Índices de Miller: (201)
Em sistemas cúbicos o plano (hkl)
é normal a direção [hkl]
1/2
41
Planos cristalográficos (cont.)
• 1, 
• 0, 1, 0
• (010)
Quando as
intersecções com os
eixos não são óbvias,
deve-se deslocar o
plano ou a origem até
obter as intersecções
corretas.
• 11, 
• 1, 1, 0
• (110)
• 1, -1, 
• 1, -1, 0
• (110)
• 1/2, 
• 0, 2, 0
• (020)
• 11, 1
• 1, 1, 1
• (111)
• 1, -1, 1
• 1, -1, 1
• (111)
42
Planos da Rede Hexagonal
c
 Os 3 eixos, a1, a2 e a3 axes
estão contidos dentro da base
planar;
 O ângulo entre eles é de 120o
 O eixo Z é perpendicular à base a
3
planar.
[h' k ' l ' ] 
[hkil]
1
i  (h  k )
a2
-1
Índices de Miller-Bravais
• 4 coordenadas
• redundância
a1
• , 1, -1, 
• 0, 1, -1, 0
• (0 1 1 0)
Face do prisma
43
Resumo
• Direções
 [uvw]
• Famílias de direções
 <uvw>
• Planos
 (hkl) (índices de Miller)
 Na hexagonal (hkil) (índices de Miller-Bravais)
i = - (h + k)
• Famílias de planos
 {hkl}
44
FAMÍLIA DE PLANOS {110}
É paralelo à um eixo
FAMÍLIA DE PLANOS {111}
Intercepta os 3 eixos
PLANOS NO SISTEMA
CÚBICO
A simetria do sistema cúbico faz com que a família de planos tenham o
mesmo arranjamento e densidade
Deformação em metais envolve deslizamento de planos atômicos. O
deslizamento ocorre mais facilmente nos planos e direções de maior
densidade atômica
PLANOS DE MAIOR DENSIDADE
ATÔMICA NO SISTEMA CCC
• A família de planos
{110} no sistema ccc é
o de maior densidade
atômica
PLANOS DE MAIOR DENSIDADE
ATÔMICA NO SISTEMA CFC
• A família de planos
{111} no sistema cfc é
o de maior densidade
atômica
Fonte: Eleani Maria da Costa
DEM/PUCRS
Densidade Atômica Planar
• Análogo ao fator de empacotamento atômico, que corresponde à
densidade volumétrica de átomos, podemos definir a densidade
atômica planar
 DAP = Área Total de Átomos/Área do Plano
• Exemplo
 Calcule a DAP dos planos {100} na rede CFC
Número total de átomos = 1 + 4*1/4 = 2
Área total de átomo = 2 x Área de 1 átomo = 2R2
Área do Plano = a2 e 4R = a2 => a = 2R2
1 átomo
1/4 de átomo
DAP = 2R2/a2 = 2R2/8R2 = /4785
50
Densidade Atômica Linear
• Análogo à DAP podemos definir a densidade atômica linear
 DAL = Comprimento Total de Átomos/Comprimento de uma direção
(igual ao fator de empacotamento em uma dimensão)
Fração de átomos interceptados por uma linha
• Exemplo
 Calcule a DAL das direções <100> na rede CFC
Número total de átomos = 1 + 1 = 2
Comprimento total de átomo = 2 x Raio de 1 átomo = 2R
Comprimento da Direção = a e 4R = a2 => a = 2R2
DAL = 2R/a = 2R/ 2R2 = 1/2 .77
1/2 átomo
51
Planos e Direções Compactas
• Como já vimos, as redes CFC e HC são as mais densas do ponto
de vista volumétrico.
• Por outro lado, em cada rede, existem planos e direções com
valores diferentes de DAP e DAL.
• Em cada rede, existe um certo número de planos e direções
compactos (maior valor de DAP e DAL)
As direções compactas estão contidas em planos compactos
Estes planos e direções serão fundamentais na deformação
mecânica de materiais.
A deformação mecânica normalmente se dá através do
deslizamento de planos.
52
Sistemas de deslizamento
•O deslizamento ocorrerá mais facilmente em certos planos e
direções do que em outros.
•Em geral, o deslizamento ocorrerá paralelo a planos compactos,
que preservam sua integridade.
•Dentro de um plano de deslizamento existirão direções
preferenciais para o deslizamento.
•A combinação entre os planos e as direções forma os sistemas de
deslizamento (slip systems), característicos das diferentes estruturas
cristalinas.
53
Sistemas de deslizamento (cont.)
 O deslizamento é mais
provável em planos e
direções compactas
porque nestes casos a
distância que a rede
precisa se deslocar é
mínima.
 Dependendo da simetria
da estrutura, outros
sistemas de
deslizamento podem
estar presentes.
Plano não
denso
Distância
Plano denso
Distância
54
Sistemas de deslizamento (cont.)
Deslizamento de um plano compacto
Pequeno deslizamento  Pequena energia
 Mais provável
Deslizamento de um plano não compacto
Grande deslizamento  Grande energia
 Menos provável
55
Sistemas de deslizamento (cont.)
Direções de
Deslizamento
Número de
Sistemas de
Deslizamento
CCC
{110}
{211}
{321}
<111>
6x2 = 12
12
24
-Fe, Mo, W
CFC
{111}
<110>
4x3 = 12
Al, Cu,
-Fe, Ni
HC
{0001}
{1010}
{1011}
<1120>
3
3
6
Cd, Mg, Ti, Zn
Estrutura
Cristalina
Planos de
Deslizamento
Geometria da
Célula Unitária
Exemplos
A tabela mostra os sistemas de deslizamento das 3 redes básicas. Em vermelho aparecem os sistemas
principais. Em cinza aparecem os secundários. Por exemplo: Como a rede CFC tem 4 vezes mais sistemas
56
primários que a HC, ela será muito mais dúctil.
57
Determinação da estrutura
• Pergunta básica
 Como se pode determinar experimentalmente a estrutura
cristalina de um material ?
• Uma boa resposta
 Estudar os efeitos causados pelo material sobre um feixe de
radiação.
• Qual radiação seria mais sensível à estrutura ?
 Radiação cujo comprimento de onda seja semelhante ao
espaçamento interplanar (da ordem de 0.1 nm).
 Difração de raios-x.
58
O espectro eletromagnético
luz visível
microondas
raios-x
raios gama
UV
infravermelho
ondas de rádio
Comprimento de onda (nm)
Como os raios-x têm comprimento de onda da ordem da
distância entre os planos atômicos, eles sofrem difração
quando são transmitidos ou refletidos por um cristal.
59
DETERMINAÇÃO DA ESTRUTURA
CRISTALINA POR DIFRAÇÃO DE RAIO X
• O FENÔMENO DA DIFRAÇÃO:
• Quando um feixe de raios x é
dirigido à um material cristalino,
esses raios são difratados pelos
planos dos átomos ou íons dentro do
cristal
60
Difração (revisão ?)
• Difração é um fenômeno de interferência
Interferência Construtiva
+
=
-Considere as ondas 1 e 2 com o
mesmo comprimento de onda (), em
fase no ponto o-o’.
- Quando dispersas (1’ e 2’) se a
diferença no comprimento da trajetória
corresponde a um número inteiro de
comprimento de onda, encontram-se,
ainda em fase, diz-se que elas se
reforçam mutuamente ( interferem
constritivamente uma na outra.
+
Interferência Destrutiva
61
A lei de Bragg
Raios-X
incidentes
Raios-X
difratados
Planos
atômicos
= distância
interplanar


 
d
A
C
B
Diferença de caminho dos dois raios:
AB + BC = 2AB = 2d sen
Condição para interferência construtiva
2d sen = n 
onde n é um número inteiro e
 é o comprimento de onda do raio-x
dhkl=
a
(h2+k2+l2)1/2
Válido
para
sistema cúbico
62
Métodos de difração de raios-X
 Laue
 Uma amostra mono-cristalina é exposta a raios-X com vários comprimentos
de onda (poli-cromático).
 A lei de Bragg é satisfeita por diferentes conjuntos de planos, para
diferentes comprimentos de onda.
 Para cada condição satisfeita, haverá uma forte intensidade difratada em um
dado ângulo.
Filme ou detetor
Colimador
Fonte de
raios-X
policromático
180°-2
Mono-cristal
63
TÉCNICAS DE DIFRAÇÃO
• Técnica do pó:
É bastante comum, o material a ser analisado
encontra-se na forma de pó (partículas finas
orientadas ao acaso) que são expostas à radiação
x monocromática. O grande número de
partículas com orientação diferente assegura que
a lei de Bragg seja satisfeita para alguns planos
cristalográficos
O DIFRATOMÊTRO DE
RAIOS X
•
•
•
Fonte •
T= fonte de raio X
S= amostra
C= detector
O= eixo no qual a amostra e o
detector giram
Métodos de difração de raios-X
 Difratômetro (ou método do pó)
 Uma amostra poli-cristalina é exposta a raios-X monocromático.
O ângulo de incidência varia continuamente.
 Para certos ângulos, a Lei de Bragg é satisfeita para algum plano
de algum dos mono-cristais, em orientação aleatória.
Colimador
Colimador
Detetor
Fonte de
raios-X
monocromático
Amostra
policristalina
(pó)
66
• Ex: Espectro de difração para Al (Difratograma)
 = 0.1542 nm (CuK)
Ângulo (2)
Uma amostra desconhecida é analisada e seus picos comparados com os de
materiais conhecidos e tabelados, permitindo assim a identificação do
material.
67
A lei de Bragg (cont.)
• A lei de Bragg relaciona quatro variáveis:
 2d sen = n 
  - o comprimento de onda dos raios-X
– pode assumir apenas um valor (monocromático)
– pode assumir muitos valores - raios-X “brancos”
(policromáticos)
 d - o espaçamento entre os planos
– pode variar aleatoriamente em função da posição relativa dos diversos
mono-cristais que formam uma amostra poli-cristalina
  - o ângulo de incidência dos raios-X
– pode variar continuamente dentro de uma faixa
– pode assumir diferentes valores, em função do conjunto de planos que
difrata o feixe de raios-X
 n - a ordem da difração
68
Para o ferro com estrutura cristalina CCC, compute (a) o espaçamento Interplanar,e (b)
o ângulo de difração para o conjunto de planos (220). O parâmetro de rede para o ferro
equivale a 0,2866 nm (2,866 A ). Ainda, admita que uma radiação monocromática como
comprimento de onda de 0,1790 nm (1,790 A ) seja usada, e que ordem de reflexão seja
de 1.
O valor do espaçamento interplanar d é determinado através da equação:
d
a= 0,2866 nm, e
a
h2  k 2  l 2
d
h = 2, k = 2 e l = 0, uma vez que estamos
Considerando os planos (2 2 0)
0 ,2866 nm
 0 ,1013nm ( 1 ,013
( 2 )2  ( 2 )2  ( 0 )2
Aplicando a lei de Bragg;
sen 
A)
n = 2 d sen
n ( 1 )( 0 ,1790 nm

 0 ,884
2d ( 2 )( 0 ,1013nm )
  sen  1 ( 0 ,884 )  62 ,13
O ângulo de difração equivale a 2
2 = (2) (62,13º) = 124,26º
69
Raios X de um comprimento de onda desconhecido são difratados 43,4º por cobre CFC, o
qual
Possui um parâmetro celular a de 0,3615 nm. Determinações em separados indicam que
esta
Linha de difração para o cobre é de 1° ordem (n =1) para d111.
a) Qual o comprimento de onda dos raios X ?
b) Os mesmos raios X são usados para analisar tungstênio (CCC). Qual o ângulo, 2,
para as linhas de difração de 2° ordem (n =2) de espaçãmento d010 ?
Sendo: 2 = 43,4°, e usando as equações :
d
a
n = 2 d sen
h2  k 2  l 2
n =2 [
(1)=2[
a
h2  k 2  l 2
]sen
0 ,3615 nm
] sen 21,7  0 ,1543nm
12  12  12
70
b)
Os mesmos raios X são usados para analisar tungstênio (CCC). Qual o ângulo, 2, para as
linhas de difração de 2° ordem (n =2) de espaçãmento d010 ?
Do apendice B ( Van vlack)
RW= 0,1376 nm
(accc)=4R/3
aw= 4( 0,1367nm/ 3 = 0,3157 nm
n =2 [
a
h2  k 2  l 2
]sen
sen = 2(0,154)nm0+1+0/(2)(0,3157nm)
2 = 58,4°
71