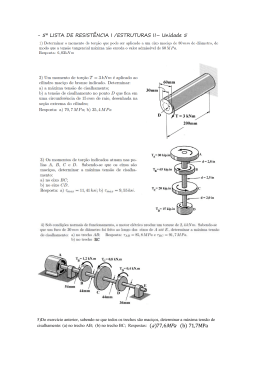
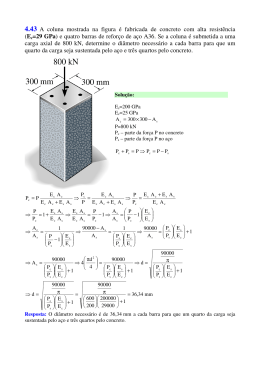
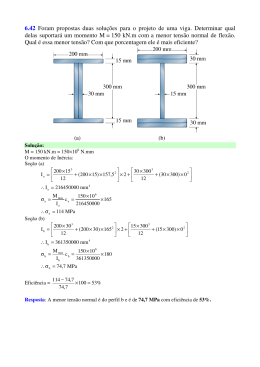
ENG 1007 – INTRODUÇÃO À MECÂNICA DOS SÓLIDOS
Segunda prova – turma D
16/05/2013
a
1 Questão (2,5 pontos)
Um ventilador está fixado ao teto por meio de uma haste de suporte feita de um tubo circular com raio
externo re = 20 mm . Sua seção transversal tem momento polar de inércia J = 6,1×10−8 m4 , e o material
homogêneo e isótropo tem tensão de cisalhamento admissível τ adm = 20 MPa . Esse equipamento gira a
uma velocidade de 1200 rpm . Calcular a potência do ventilador em hp, para fator de segurança à torção
igual 2,57.
T (x )Gρ
; 1 hp=746 W.
P = 2π nT ; τ (x, ρ ) =
r (x )
2π ∫ Gρ 3 dρ
0
Resposta:
FS =
τ adm
20
=
= 2,57 ⇒ τ máx = 7,78 MPa
τ máx τ máx
τ máx J 7,78 × 106 × 6,1× 10 −8
T re
= 7,78 MPa ⇒ T =
=
= 23,73 kN .m
re
0,02
P
746 P
T=
=
= 23, 75 Nm ⇒ P = 4, 00 hp
2π n 2π × 1200
60
2a Questão (2,5 pontos)
τ máx =
J
O eixo formado pelos segmentos AB (peça de aço maciço), BC (tubo de aço e núcleo de alumínio) e
CD (tubo de aço com núcleo vazio), tal como mostra a Figura, está solicitado a torção pura. Pede-se
A) esboçar o diagrama de momento de torção, com os valores numéricos em cada trecho e o sinal;
B) verificar se a tensão máxima de cisalhamento do aço no trecho AB é menor que a tensão
máxima admissível τ adm = 400MPa ;
C) calcular o ângulo de rotação na extremidade livre.
DADOS:
T ( x)Gρ
G AL = 28 GPa ; G AÇO = 84 GPa ; T = 200 kN .m ;
τ ( x, ρ ) =
r( x)
2π ∫ G ρ 3 d ρ
r = 10 cm
r = 8 cm
0
alumínio
aço
T
A
L
L=1m
B
L
e
i
T
T
L=1m
C
L
L=1m
D
L
Resposta:
A) Todos são positivos
3T = 600 kN .m; 2T = 400 kN .m; T = 200 kN .m
dϕ =
T dx
r
2π ∫ G ρ 3dρ
0
B) Tensão máxima de cisalhamento no aço
τ máx =
3Tre
π
4
e
=
3 × 200 × 10 6 × 100
π
= 382 MPa < 400MPa→ ok!
4
r
× 100
2
2
C) Ângulo de rotação na extremidade livre.
600 L
400 L
200 L
ϕ AD =
+
+
π
π
G AÇO re4 − ri 4
G AÇO re4
G AL ri 4 + G AÇO re4 − ri 4
2
2
6
600 ×1× 10
400 × 1×106
200 × 1× 106
φ AD =
+
+
π
π
π
84 × 0,14
28 × 0, 084 + 84 ( 0,14 − 0, 084 ) 
84 ( 0,14 − 0, 084 )

2
2
2
[
ϕ AD =
(
)]
(
)
600 × 10 6 400 × 10 6 200 × 10 6
+
+
= 0,113 rad
0,01319 0,009591 0,00790
3a Questão (2,5 pontos)
Um tubo feito de bronze (G = 38 GPa) tem seção transversal retangular como mostrado na figura. Para
os dois torques aplicados, mostrados à direita, qual é a tensão de cisalhamento média nos pontos A e B?
Além disso, qual é o ângulo de torção da extremidade C? O tubo é fixo em E.
τ=
dϕ =
Resposta:
T
2 Amt
T ⌠ ds

dx
4 Am2 G ⌡Cm t
O torque atuante no trecho CD é TCD = 60 N .m . No trecho DE, TDE = (60 − 25) N .m = 35 N .m .
A área média A m do tubo é igual à do retângulo (40 − 5) × (60 − 3)mm 2 = 0, 001995m 2 .
35 Nm
a) τ A =
= 1, 754 MPa ;
2 × 0, 001995m 2 × 0, 005m
35 Nm
b) τ B =
= 2,924 MPa ;
2 × 0, 001995m 2 × 0, 003m
( 60 Nm × 0,5m + 35 Nm ×1,5m ) × ( (40 − 5) / 3 + (60 − 3) / 5) × 2 = 0, 00629 rad .
c) ∆ϕCE = ∆ϕCD + ∆ϕ DE =
4 × 0, 0019952 m 4 × 38 ×109 N / m 2
4a Questão (2,5 pontos)
Uma barra de aço é engastada em uma de suas extremidades e carregada por um torque T na outra (ver
figura). O módulo de elasticidade transversal é G = 79 GPa. Determine:
b = 1 cm
a = 3 cm
b = 1 cm
a = 1 cm
T
30 cm
C
20 cm
B
A
a) Os coeficientes α e β para os dois trechos (CB e BA) da barra.
b) O torque máximo T que pode ser aplicado, para uma tensão máxima admissível τadm = 50 MPa.
c) O ângulo de torção (em graus) na extremidade A, supondo T = 8 N m.
TL
T
Para solução, considere τ máx =
e φ max =
, onde α e β podem ser obtidos abaixo:
2
α ab
β a b3 G
1,0
0,208
0,141
a/b
α
β
1,5
0,231
0,196
2,0
0,246
0,229
2,5
0,256
0,249
3,0
0,267
0,263
4,0
0,282
0,281
5,0
0,292
0,291
10,0
0,312
0,312
∞
0,333
0,333
Resposta:
a) 0,5 pontos
Trecho CB: α = 0,267 e β = 0,263
Trecho BA: α = 0,208 e β = 0,141
b) 1,0 ponto
τ máx =
T
3
= 50.106 → T = ( 50.106 )(α a b 2 ) → T = ( 50.106 ) ( 0, 208 )( 0, 01) → T = 10, 4 Nm
2
α ab
c) 1,0 ponto :
ϕA =


T  LCB
LBA 
8.0
0,3
0, 2
+
=
+




b3 G  β CB aCB β BA aBA  ( 0, 01)3 ( 79.109 )  ( 0, 263)( 0, 03) ( 0,141)( 0, 01) 
∴ ϕ A = 0, 0182 rad = 1, 0136o