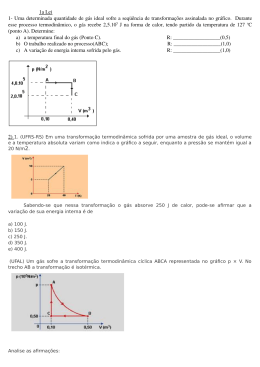
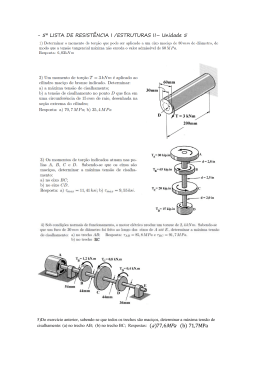
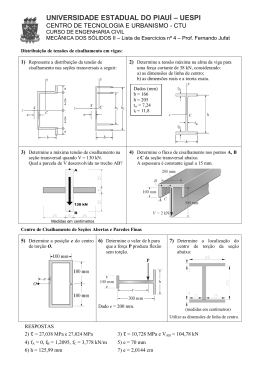
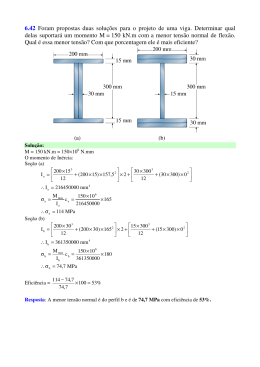
ENG 1007 – INTRODUÇÃO À MECÂNICA DOS SÓLIDOS
Segunda prova – turma B
17/10/2013
a
1 Questão (2,5 pontos)
Para o eixo da figura abaixo, determine:
1- as tensões cisalhantes máximas nos trechos AB e BC,
2- os ângulos de rotação das seções B e C.
Sabe-se que L =10cm, o trecho AB é sólido com diâmetro D = 4cm e o trecho BC é oco com diâmetros
externo de = 2cm e interno di = 0,5cm. O torque em B é TB = -10kNcm e em C é TC = -2kNcm. O
módulo de elasticidade transversal do material é G= 10GPa.
Tr
τ=
J
J =
π
2
( re4 − ri 4 )
φB − φ A =
T AB L AB
GJ
Resposta
12 × 2
= 0, 9549kN cm 2 = 9, 549 MPa
4
π 2× 2
2 ×1
=
= 1, 278kN cm 2 = 12, 78MPa
π 2 × (14 − 0, 254 )
AB
τ máx
=
BC
τ máx
−12 × 10
= −0, 00477 rad
π 2 × 24 ×10 ×102
−2 × 10
ϕC = ϕ AB + ϕ BC = −0, 00477 +
− 0, 00477 − 0, 01278 = −0, 01756rad
4
π 2 × (1 − 0, 254 ) ×10 ×102
ϕ B = ϕ AB =
2a Questão (2,5 pontos)
Um eixo vazado de aço (G = 77 GPa) de 5m de comprimento e raios interno e externo de 12,5mm e
30mm, respectivamente, gira a 180rpm. Sabendo que o ângulo de torção entre suas extremidades é de
30, determinar a potência que está sendo transmitida e a máxima tensão de cisalhamento que ocorre.
T dx
T ( x )Gρ
; dφ =
P = 2π nT ; τ (x, ρ ) =
r
r(x)
2π ∫ Gρ 3 dρ
2π ∫ Gρ 3 dρ
0
0
Resposta
3π
T × 5m
∆ϕ =
=
⇒ T = 1, 026kNm
4
4
180 π 2 × ( 30 − 12,5 ) ×10−12 m 4 × 77 ×109 Pa
P = 2π
τ máx =
180
1, 026 = 19, 335kW
60
1, 026 × 30 ×10−3
π 2 × ( 304 − 12,54 ) ×10−12
= 24,19 MPa
3a Questão (2,5 pontos)
Um tubo de alumínio tem espessura de 5mm e as dimensões externas da seção transversal mostradas.
a) Determinar a tensão de cisalhamento média máxima nele desenvolvida.
b) Se o tubo tiver comprimento de 5m, qual será o ângulo de torção da extremidade? Gal = 28GPa .
τ=
dϕ =
Resposta
Diagrama de torques:
T
2A m t
T ⌠ ds

dx
4A 2m G ⌡Cm t
−145
−280
Am = (100 − 5) × (150 − 5) × 10−6 m 2 = 0,013775m 2 ;
⌠


⌡C m
ds
Cm = 2 [(100 − 5) + (150 − 5) ] 5 = 96
t
280 Nm
= 2,0327 MPa
2 × 0,013775m 2 × 5 × 10−3 m
96
b) ∆ϕ =
( −280 × 2 − 145 × 3) = −0,004495rad
2
4 × ( 0,013775m 2 ) × 28 × 109
a) τ máx =
4a Questão (2,5 pontos)
Um eixo está submetido a torção, conforme mostrado na Figura, para T = 10kNm. O trecho AB tem
seção transversal quadrada cheia, de lado d = 0,1m. O trecho BC tem seção transversal quadrada de
parede fina, de lado d = 0,1m e espessura t = 0,001m. O módulo de elasticidade transversal do material
é G = 80GPa. Calcular:
a) a rotação da seção C em relação à seção A;
b) a máxima tensão de cisalhamento no tubo.
t = 0,001 m
T
5T
A
ℓ = 1m
B
3ℓ = 3 m
C
d = 0,1 m
Fórmulas para eixo de seção transversal retangular:
T
T
τ máx =
T
αab 2
a/b
α
β
∆φ =
1,0
0,208
0,141
TL
β ab3G
a
τmáx
b
Tabela para obtenção dos coeficientes α e β
1,2
1,5
2,0
2,5
3,0
4,0
5,0
0,219 0,231 0,246 0,258 0,267 0,282 0,291
0,166 0,196 0,229 0,249 0,263 0,281 0,291
10,0
0,312
0,312
∞
0,333
0,333
Fórmulas para eixo de seção transversal de parede fina:
τ=
T
2A m t
dφ =
T ⌠ ds
dx

4A 2m G ⌡C m t
Resposta
Tem-se por equilíbrio um torque de 6T aplicado ao trecho AB e de T aplicado ao trecho BC. O trecho
AB tem seção transversal quadrada cheia, portanto de lados a = b = d. Obtém-se para a/b = 1 na tabela
que α = 0,208 e β = 0,141 . O trecho BC tem seção transversal quadrada de parede fina, de lado d =
0,1 m, espessura t = 0,001 m, perímetro Cm = 4d = 0,4 m e área compreendida pelo perímetro
Am = d 2 = 0,01 m 2 .
a) Rotação da seção C em relação à seção A: φ AC = φ AB + φ BC =
6Tℓ
T3ℓ 4d
+
4
βd G 4 × d 4 G t
6 × 10 × 10 3 × 1
10 × 10 3 × 3 × 1 4 × 0,1
+
= 0,05319 + 0,375 = 0,42819 rad
0,141 × 0,14 × 80 × 10 9 4 × 0,14 × 80 × 10 9 0,001
6T 6 × 10 × 10 −3
b) Tensão máxima no trecho AB: τ = 3 =
= 288,462 MPa
αd
0,208 × 0,13
10 ×10 −3
T
∴τ máx = 500 MPa
Tensão no trecho BC: τ = 2 =
= 500 MPa
2d t 2 × 0,12 × 0,001
∴ φ AC =