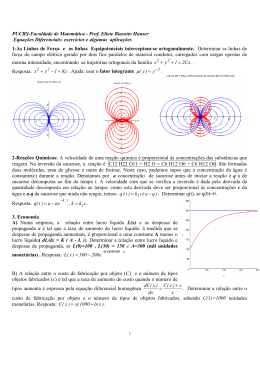
Simulação no Tempo: Esquemas de Solução
Sistema de Equações Não Lineares Algébrico Diferencial
 
x  f  x, y 

0  g x, y 

x  f x, y 
  wr
w  2 H Pm  Pe 

  w  w
r


1

E

E fd  xd  xd I d  Eq
 q
Tdo

 
1
E

K a Vref  V1   E fd
 fd
Ta



0  g x, y 




 I d , I q 

I re , I im

 Pe  Vd .I d  Vq .I q  

V
,
V


Vre , Vim

 d q

 I  y .E  E  , E  


0, Eq
1
eq
1
re
im


P2  j.Q2
y

I2  0
 2
o 2
V2




P3  j.Q3
P3  j.Q3 

 I 3  y3 
.V3
 y3 
2
o 2


V3
V3




I   Y  V 

x  f x, y 
0  g x, y 
Os esquemas de solução baseiam-se no método de
integração numérico aplicado as equações diferenciais e
no modo de interação entre os sistemas algébrico e
diferencial
Método de
Integração
Esquema Básico
Alternado
Simultâneo
Explícito
AE
SE
Implícito
AI
SI
 Esquema Alternado: resolve-se separadamente, em cada passo de integração,
o sistema algébrico e o diferencial alternando-se as respectivas soluções.
 Esquema Simultâneo: as equações diferenciais e algébricas são resolvidas
simultaneamente como um único sistema de equações, em geral, pelo método
de Newton (ou baseado no método de Newton)
As fórmulas implícitas de integração numérica tem apresentado melhores
resultados, sendo o método trapezoidal o mais utilizado
Equações Diferenciais
Eqs. Algébricas a Diferenças

 
h
xt1   x to    f xt1  , t1  f x to  , to
2
=0

wr
Pm  Pe  D  w
w
2H
t  wr
wr

wt1   wto    
Pmt   Pe t1  
Pmt   Pe to  
1
o
2  2H
2H

wr  t
wr  t
wt1  
 Pmt   Pe t1  
 Pmt   Pe to   wto 
1
4H
Ho
4







wr  t
wt1  
 Pmt1   Pe t1    to 
4H



 t o 


  w  wr


1
E q 
E fd  xd  xd I d  Eq
Tdo

E fd

1

K a Vref  V1   E fd
Ta


t
 wt1    to 
1
2
t

Eq t1  
E fd t1   xd  xd I d t1    to 
2Tdo  t
 t  

E fd t1  



t
 K a V1t1   to 
2Ta  t
Resumo da Modelagem:
t
passo de integração

 Eqs. Diferenciais Algebrizadas
x  f x, u 

wr  t

w

Pm t1   Pe t1    to 
 t1 
4H

  t  w  
t o 
 t1  2 t1 

t
 Eq t1  
E fd t1    xd  xd I d t1    to 
2Tdo  t


t
 E fd t1  
 K a  V1t1    to 

2Ta  t
 I d   Eq  Vre1. cos  Vim1. sin  xd

 I q  Vre1. sin   Vim1. cos  xq

 Pe  Ed .I d  Eq .I q  xq  xd I d .I q
 I1  yeq .E 



P3  j.Q3 
  V3
 I 3   y3 
2
V3




I   Y  V 



 Equações de Interface
u  g x,V 
 Eqs. da Rede Elétrica + Cargas
I E ,V   Y V



Esquema Alternado Implícito:
o esquema alternado consiste
basicamente em transformar as equações diferenciais em equações algébricas a
diferenças, através de um método de integração, e resolvê-las iterativamente e
alternadamente com as equações originalmente algébricas
Algoritmo Alternado Implícito:
Inicialização: dx/dt=0
w, , E’q
Para: (t=0; t; Tfinal)
xo(t) = f (x(t),u(t),x(t- t),u(t- t))
k=0
Enquanto: || x(t) ||2 >
Resolva: I (E(t),V(t)) = [ Y ] . V(t)
uk(t) = g (E(t),V(t))
Resolva xk+1(t) = f (xk (t),uk (t),xk (t- t),uk (t- t))
xk+1 (t) = | xk+1 (t) - xk(t) |
k = k+1
 O cálculo de x(t) é iterativo devido a adoção de um método de integração
implícito
 As injeções de corrente são, em geral, funções não lineares de V(t) para as
cargas, assim a equação da rede elétrica também deve ser resolvida
iterativamente
Esquema Alternado Entrelaçado Implícito (AEI): uma alternativa a este
esquema é obtida relaxando-se os requisitos de convergência na solução das
equações da rede elétrica, por exemplo realizando-se somente uma iteração.
Neste caso os processos iterativos diferencial e algébricos são entrelaçados e
apresentam melhor desempenho computacional que o AI clássico