Unidade IV – Probabilidade
4.1 Conceitos fundamentais e propriedades
(probabilidade condicional, independência de eventos
e teorema de Bayes).
4.2 Variáveis aleatórias: conceito, variáveis aleatórias
discretas e contínuas, função de distribuição de
probabilidade, esperança, variância e desvio padrão.
4.3 Distribuições discretas: Binomial, Hipergeométrica e
Poisson.
4.4 Distribuições contínuas: Uniforme, Normal, Binomial
com aproximação da Normal e Exponencial.
4.1 Principais conceitos
Probabilidade: é uma medida que exprima a incerteza presente em
afirmações tais como “É possível que chova amanhã” ou “Não há chance de
vitória”, em termos de uma escala numérica que varie do impossível ao
certo.
O conceito de probabilidade é fundamental para o estudo de situações
em que os resultados são variáveis, mesmo quando mantidas
inalteradas as condições de sua realização.
Exemplo:
1) jogando-se um dado, temos 6 resultados possíveis de cada vez
2) A observação do sexo das crianças nascidas numa maternidade durante
um mês conduz a dois resultados possíveis em cada caso: menino ou
menina.
3) Jogando-se duas moedas os resultados possíveis de cada vez são: cara
e cara, cara e coroa, coroa e cara, coroa e coroa.
•
•
Em ambos os casos, embora não sejamos capazes de afirmar de
antemão qual resultado particular acontecerá, temos condição de
escrever todos os resultados possíveis do experimento.
A sua repetição contínua mostra uma certa regularidade nos resultados
o que nos permite estudar o fenômeno, apesar da incerteza nele
presente.
4.1 Principais conceitos
Experimento aleatório: é qualquer processo de coleta de dados relativos a
um fenômeno que acusa variabilidade em seus resultados.
Evento: é um subconjunto de um espaço amostral. Quando constituído de
apenas um elemento é chamado de evento simples e quando constituído
de mais de um elemento é chamado de evento composto.
Espaço amostral: é o conjunto de todos resultados possíveis de um
experimento. Denotado por E.
Quando o espaço amostral consiste em um número finito ou infinito
enumerável de eventos é chamado espaço amostral discreto, se consistir
em todos os números reais de um intervalo é um espaço amostral contínuo.
Exemplos de Espaço amostral:
1) No lançamento do dado o espaço amostral E={1, 2, 3, 4, 5, 6}
2) No lançamento de duas moedas o espaço amostral c=cara e co=coroa
E={cc, cco, coc, coco}.
3) No nascimento dos bebês E={menino, menina}
4.1 Principais conceitos
1) Definição clássica de Probabilidade: Só se aplica para espaços amostrais
que os eventos simples são igualmente possíveis. Esse é o caso da maioria
das aplicações de probabilidades aos jogos de azar.
Suponha que um experimento tenha n eventos simples diferentes, cada um dos
quais com a mesma chance de ocorrer. Se o evento A pode ocorrer em s
dentre as n maneiras então a Probabilidade de A acontecer é:
P( A) 
númerode maneirascomoA pode ocorrer s

númerode eventossimplesdiferentes
n
2) Definição frequentista de Probabilidade
Realize ou observe um experimento um grande número de vezes e conte
quantas vezes o evento A ocorre efetivamente. Então a probabilidade de A
acontecer é
P( A) 
númerode ocorrências de A
númerode repetiçõesdo experimento
4.1 Principais conceitos
Lei dos grandes números: Se repete um experimento um grande número
de vezes a probabilidade pela freqüência relativa de um evento tende para
a probabilidade teórica.
A união de dois eventos: é o evento que consiste em todos os resultados
que estão contidos em cada um dos dois eventos. Denotamos a união por
E1UE2. P(E1 ou E2 )= P(ocorrência de E1 ou de E2 ou de ambos)=P(E1UE2).
A interseção de dois eventos: é o evento que consiste em todos os
resultados que estão contidos nos dois eventos simultaneamente.
Denotamos a interseção por E1∩E2. P(E1 e E2) = P(ocorrência de E1 e E2
simultaneamente) = P(E1∩E2).
O complemento de um evento em um espaço amostral: é o conjunto dos
resultados no espaço amostral que não estão no evento. Denotamos o
complemento do evento E por E’. A notação Ec é também usada em outra
literatura para denotar complemento.
P(E1’)=1-P(E1)
P(E2’)=1-P(E2)
4.1 Principais conceitos
Axiomas de probabilidade:
Asseguram que as probabilidades atribuídas a um experimento podem ser
interpretadas como freqüências relativas. As probabilidades são atribuídas
como base no nosso conhecimento do sistema sob estudo.
a) P(E)=1
É uma conseqüência do fato de que um resultado do espaço amostral
ocorre em cada tentativa de um experimento.
b) 0 ≤P(A) ≤1
c) Para dois Eventos E1 e E2 com E1∩E2 = Ø (E1 e E2 são mutuamente
excludentes)
P(E1UE2)=P(E1)+P(E2)
Para quaisquer eventos não mutuamente excludentes
P(E1UE2)=P(E1)+P(E2)-P(E1∩E2)
4.1 Principais conceitos
Princípio Fundamental da Contagem
Quais são as chances de ganhar na loteria?
No Brasil, devemos escolher 6 números entre 1 e 60. Se sair a mesma combinação de 6
números escolhida o apostador receberá milhões de reais!!!
•
•
•
P(A) = s/n onde s é o número de maneiras como A ode ocorrer
n é o número total de resultados possíveis.
Como calcular o número total de possibilidades?
1) Regra Fundamental da Contagem
Dados dois eventos, o primeiro dos quais pode ocorrer de m maneiras distintas e o segundo
pode ocorrer de n maneiras distintas, então os dois eventos conjuntamente podem
ocorrer de mxn maneiras distintas.
6! = 6 . 5. 4. 3. 2. 1 e 0! = 1
4.1 Principais conceitos
Contagem
2) Permutação
P(n) = n! = n . (n-1). (n-2). (n-3). ...1
Quantas maneiras podemos organizar um grupo de n objetos de maneiras distintas. (Essa regra
traduz o fato de que o primeiro objeto pode ser escolhido de n maneiras diferentes, o segundo
objeto pode ser escolhido de n-1 maneiras distintas e assim por diante...)
Notação: O símbolo fatorial! Denota o produto dos inteiros positivos em ordem decrescente, por
exemplo: 4!= 4 . 3. 2. 1
6! = 6 . 5. 4. 3. 2. 1 e 0! = 1
n Ap 
n!
(n  p)!
4.1 Principais conceitos
Contagem
3) Arranjos sem repetição
O número de arranjos (ou seqüências) de r elementos escolhidos dentre n elementos sem
repetição é:
n Ap 
n!
(n  p)!
A regra dos arranjos exige as seguintes condições:
Devemos ter um total de n elementos diferentes (A regra não se aplica se alguns dos elementos
são idênticos)
Devemos selecionar r dentre os n elementos (sem repetição)
Ordenações distintas dos mesmos elementos devem ser consideradas arranjos diferentes.
4.1 Principais conceitos
Contagem
“Quando empregamos os termos arranjos ou seqüência está implícito que a ordem
deve ser levada em conta”. O arranjo pode ser considerado como uma extensão da
Regra Fundamental da Contagem.
•
Exemplo: No planejamento de um programa noturno de uma rede de televisão,
devem ser escolhidos 6 shows dentre 30 disponíveis. Quantas programações
diferentes são possíveis?
30!
30.29.28.27.26.25.24!

 427.518.000
30 A6 
(30  6)!
24!
4.1 Principais conceitos
Contagem
4) Arranjos com repetição
Quando alguns elementos são idênticos, se há n elementos com n1 iguais a n2 iguais
a nk, o número de permutações (arranjos com a totalidade de elementos) é:
•
•
•
A
n!
n1!.n2!.n3!...nk !
Exemplo: Na seqüência DDDDRRRRR temos n=9 elementos n1=4 iguais e n2=5
iguais. O número de permutações é
A
9!
9.8.7.6.5!

 126
4!.5! 5!.4.3.2.1
4.1 Principais conceitos
Contagem
5) Combinação
O número de combinações de r elementos extraídos de um conjunto de n elementos
diferentes é:
•
n Cr 
n!
(n  r )!r!
A regra dos combinações exige as seguintes condições:
• Devemos ter um total de n elementos diferentes
• Devemos selecionar r dentre os n elementos (sem repetição)
• Devemos considerar como uma mesma combinação quando os mesmos elementos são
ordenados de formas diferentes. Por exemplo (SFS, SSF, FSS)
“Quando empregamos os termos combinação a ordem não deve ser levada em conta”.
4.1 Principais conceitos
Contagem
n Cr 
5) Combinação
•
•
n!
(n  r )!r!
Exemplo: Qual a probabilidade de ganhar na Mega-Sena?
As possibilidades de combinação de 6 números entre os valores de 1 a 60 são
calculadas através da combinação, pois a ordem deles não importam.
60!
60.59.58.57.56.55.54!

 50.063.860
(60  6)!6!
54!6.5.4.3.2.1
1
Probabilidade de acertarcom um a aposta 
 1,99.108
50.063.860
60 C6 
4.1 Principais conceitos
Contagem
Qual a probabilidade de ganhar na Mega-Sena ao jogar 7 números entre os valores de 1 a
60? Qual a probabilidade de ganhar na quina ou na quadra ao jogar 7 números?
Através da distribuição hipergeométrica conseguiremos
calcular estas probabilidades!!!! Que faz parte a
matéria de Distribuições de variáveis aleatórias
discretas!!!!!
4.1 Propriedades
Regra da Adição
P(A ou B )= P(ocorrência de A ou de B ou de ambos)
P(A ou B) = P(A)+P(B)-P(AeB)
• P(AUB) = P(A) + P (B) – P (A∩B)
• Se A e B são mutuamente exclusivos P(AUB) = P(A) + P (B)
Considere três eventos A, B e C
• P(AUBUC)=P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C)
Considere uma coleção de eventos E1, E2, E3, ..., Ek é denominada mutuamente
excludente se para todos os pares Ei ∩ Ej = Ø para todo i,j=1, 2,..., k
• P(E1UE2UE3U...Ek)=P(E1)+P(E2)+...+P(Ek)
•
k
k
i 1
i 1
P(U )   P( Ei )
4.1 Propriedades
Probabilidade Condicional
A probabilidade condicional de um evento B, dado um evento A, denotada como:
P( A \ B) 
P( A  B)
, para P( B)  0
P( B)
P( B \ A) 
P( A  B)
, para P( A)  0
P( A)
Regra da Multiplicação
A probabilidade da interseção do evento A e B, denotada como:
• P(A∩B)=P(A\B).P(B) = P(B\A).P(A)
Se A e B são independentes P(A\B)=P(A), P(B\A)=P(B)
• P(A∩B)=P(A).P(B)
Se E1, E2,..., Ek são independentes
• P(E1∩E2 ∩..Ek)=P(E1).P(E2)...P(Ek)
4.1 Propriedades
Regra da Probabilidade Total
Para dois eventos A e B
• P(B)=P(B∩A)+P(B∩A’)
• P(B)=P(B\A).P(A)+P(B\A’).P(A’)
S
A
B∩A
B∩A’
B
A’
•Se E1, E2,..., Ek são mutuamente exclusivos (Ei ∩ Ej = Ø para todo i,j=1, 2,..., k)
e exaustivos (E1UE2U...EK=S)
• P(B)=P(B∩E1)+P(B∩E2)+...+P(B∩Ek)
• P(B)=P(B\E1).P(E1)+P(B\E2).P(E2)+...+P(B\Ek).P(Ek)
E1
B∩E1
E2
S
B
B∩E2
E3
B∩E3
Ek
B∩Ek
4.1 Propriedades
Teorema de Bayes
• Para dois Eventos A e B
P( A \ B) 
P( B \ A).P( A)
, para P(B)  0
P( B)
• Para E1, E2,..., Ek eventos mutuamente excludentes (Ei ∩ Ej = Ø para todo i,j=1,
2,..., k) e exaustivos (E1UE2U...EK=S)
P( E1 \ B) 
P( B \ E1 ).P( E1 )
, para P(B)  0
P( B \ E1 ).P( E1 )  P( B \ E2 ).P( E2 )  ...  P( B \ Ek ).P( Ek )
O Teorema de Bayes é últil pois nos capacita resolver P(A\B) em termos
da P(B\A). Em alguns exemplos não temos uma tabela completa de
informação e utilizamos o Teorema de Bayes para calcular a
probabilidade condicional.
4.1 Propriedades
Teorema de Bayes
• Exemplo: Suponha que 60% dos chips de computador de uma companhia sejam
produzidos pela fábrica A e 40% pela outra fábrica (A’). Para um chip escolhido
aleatoriamente a probabilidade de provir da fábrica A é 0,60. Suponha que um chip
se revele defeituoso e que as taxas de defeitos das duas fábricas sejam de 35%
para A e 25% para A’. Determine a probabilidade do chip defeituoso provir da
fábrica A.
• A: o evento que o chip é fabricado pela fábrica A
• A’: o evento que o chip é fabricado pela fábrica A’
• B: o evento que o chip é defeituoso
• P(A)=0,60 e P(A’)=1-0,60=0,40
• P(B/A)=0,35 e P(B/A’)=0,25
• P(A/B)?
P( A \ B) 
P( B \ A).P( A)
0,60.0,35
0,21


 0,6774
P( B \ A).P( A)  P( B \ A' ).P( A' ) 0,60.0,35  0,40.0,25 0,31
Probabilidade condicional
• Exemplo: Amostras de espuma de três fornecedores são classificados com
relação a satisfazer ou não as especificações. Os resultados de 80 amostras são
resumidas a seguir:
Fornecedor
Obedece
Total
Sim
Não
1
18
2
20
2
17
3
20
3
30
10
40
Total
65
15
80
Faça A1 denotar o evento em que uma amostra seja proveniente do fornecedor1,
A2 denotar o evento em que uma amostra seja proveniente do fornecedor2,
A3 denotar o evento em que uma amostra seja proveniente do fornecedor3
e faça B denotar o evento em que uma amostra atenda as especificações.
Montar o diagrama de árvore.
Probabilidade condicional
• Faça A1 denotar o evento em que uma amostra seja proveniente do fornecedor1,
A2 denotar o evento em que uma amostra seja proveniente do fornecedor2,
A3 denotar o evento em que uma amostra seja proveniente do fornecedor3
e faça B denotar o evento em que uma amostra atenda as especificações.
Montar o diagrama de árvore.
A1
P(A1)
B
P(B\A1)
A3
A2
P(A3)
P(A2)
B’
P(B’\A1)
B
P(B\A2)
B’
P(B’\A2)
B
P(B\A3)
B’
P(B’\A3)
Probabilidade condicional
• P(A1)=20/80=0,25
• P(A2)= 20/80=0,25
• P(A3)=40/80=0,50
18
P( A1  B) 80 18
P( B \ A1 ) 


 0,9
20 20
P( A1 )
80
17
P( A2  B) 80 17
P( B \ A2 ) 


 0,85
20 20
P( A2 )
80
2
P( A1  B' ) 80 2
P( B'\ A1 ) 


 0,10
20 20
P( A1 )
80
3
P( A2  B' ) 80 3
P( B'\ A2 ) 


 0,15
20 20
P( A2 )
80
10
P( A3  B' ) 80 10
P( B'\ A3 ) 


 0,25
40 40
P( A3 )
80
30
P( A3  B) 80 30
P( B \ A3 ) 


 0,75
40 40
P( A3 )
80
A3
A2
A1
P(A1)=0,25
P(A3)=0,50
P(A2)=0,25
B
B’
P(B\A1)=0,9
P(B’\A1)=0,10
B
P(B\A2)=0,85
B’
P(B’\A2)=0,15
B
P(B\A3)=0,75
B’
P(B’\A3)=0,25
4.2 Conceitos de Variáveis aleatórias
Abordaremos os conceitos de variável aleatória, distribuição de probabilidade,
função distribuição acumulada e processos para o cálculo da média, variância e
desvio padrão de uma distribuição de probabilidade.
• Uma variável aleatória é uma variável (geralmente representada por x) que tem
um valor numérico único (determinado aleatoriamente) para cada resultado de um
experimento.
• Uma variável aleatória tem um número para cada resultado de um experimento e
uma distribuição de probabilidades que associa uma probabilidade a cada
resultado numérico de um experimento.
• Exemplos de variáveis aleatórias:
•x=número de acidentes com aviões da USAir dentre sete acidentes aéreos
selecionados aleatoriamente,
•x=número de alunos que não compareceram à aula de estatística hoje,
•x=altura de um adulto do sexo feminino selecionado aleatoriamente.
4.2 Conceitos de Variáveis aleatórias
• Empregamos o termo variável aleatória para descrever o valor que corresponde
ao resultado de determinado experimento. A palavra aleatória indica que em geral
só conhecemos aquele valor depois do experimento ter sido realizado.
• Inicialmente fizemos uma distinção entre dados discretos e dados contínuos. As
variáveis aleatórias também podem ser discretas ou contínuas, as duas definições
que seguem são consistentes com as que foram dadas anteriormente.
• Uma variável aleatória discreta ou admite um número finito de valores ou tem
uma quantidade enumerável de valores.
• Uma variável aleatória contínua pode tomar um número infinito de valores, e
esses valores podem ser associados a mensuração em uma escala contínua, de
tal forma que não haja lacunas ou interrupções.
• Quando conhecemos todos os valores de uma variável aleatória juntamente com
suas respectivas probabilidades, temos uma distribuição de probabilidades,
definida como segue. Uma distribuição de probabilidades dá a probabilidade de
cada valor de uma variável aleatória.
4.2 Conceitos de Variáveis aleatórias
• Uma distribuição de probabilidade de uma variável aleatória pode ser dada por
uma tabela, por um gráfico ou por uma fórmula. O histograma de probabilidade
permite visualizar a natureza ou a forma da distribuição.
x
P(x)=f (x)
0
0,210
x
onde x pode ser 0, 1 ou 2 define uma
3
distribuiç ão de probabilidade.
1
0,367
Para a funçãodada temos:
2
0,275
P(0)  0/3, P(1)  1/3, P(2)  2/3 e assim
3
0,115
4
0,029
 f(x)  3  3  3  1
5
0,004
6
0,000
P( x)  f ( x) 
0
1
2
Cada um dos valoresde 0  f(x)  1
0,000 X com valores possíveis x , x , ..., x a função de
Para uma 7variável aleatória
1
2
n
probabilidade é f (xi) = P(X=xi)
•
Condições para uma distribuição de probabilidades:
1) Σ f (xi) =1, onde xi toma todos os valores possíveis para i=1, 2, ..., n
2) 0≤ f (xi) ≤1
4.2 Conceitos de Variáveis aleatórias
• Função de distribuição cumulativa de uma variável aleatória discreta X, denotada
por F(x), é
F ( x)  P( X  x) 
 f ( xi )
xi  x
F ( x) satisfazer as seguintes propriedades :
0  F(x)  1 e se x  y, então F(x)  F( y )
• Média ou valor esperado de uma de uma variável aleatória X, denotado como μ ou
E(X), é
  E ( X )   x. f ( x)
x
4.2 Conceitos de Variáveis aleatórias
• Variância de uma variável aleatória X, denotada como σ2 ou V(X), é
 2  V ( X )   x   2. f ( x)   x2. f ( x)   2
x




• Desvio padrão de uma variável aleatória X, denotada como σ
   x2. f ( x)   2


4.2 Variáveis aleatórias discretas
Valor esperado de uma variável aleatória discreta é denotado por E e representa o
valor médio dos resultados. É dado por Σx .f(x):
E (X) = Σx .f(x)
• A média de uma variável aleatória discreta é o resultado médio teórico de u
numero infinito de provas.
• Podemos encarar essa média como o valor esperado no sentido de que é o valor
médio que esperaríamos de obter se as provas se prolongassem indefinidamente.
• As aplicações do valor esperado também chamado de esperança ou esperança
matemática são extensas e variadas e desempenha papel de extrema importância
em uma área de aplicação chamada teoria da decisão.
Exemplo: Suponha que a USAir detenha 20% de todas as linhas aéreas
domésticas, e que todos os vôos tenham a mesma chance de um acidente. Se a
variável aleatória x representa o número de acidentes com a USAir dentre sete
acidentes escolhidos aleatoriamente, então a distribuição de probabilidades é
dada pela tabela abaixo, suponha que repitamos o experimento que consiste em
selecionar sete acidentes e que a cada vez achemos o número de acidentes com
a USAir. Determine o número médio de acidentes com a USAir (entre sete), a
variância e o desvio-padrão.
   x.P( x)  1,398  1,4
2 
 x .P( x) 
2
2
x
P(x)
x. P(x)
x2
x2 P(x)
0
0,210
0,000
0
0,000
1
0,367
0,367
1
0,367
2
0,275
0,550
4
1,100
3
0,115
0,345
9
1,035
4
0,029
0,116
16
0,464
0,020
25
0,100
 3,066  1,3982  1,112
5
0,004
4.2 Conceitos de distribuição de probabilidade
•Uma distribuição de probabilidade é um modelo matemático que
relaciona um certo valor da variável em estudo com a sua probabilidade
de ocorrência.
•Há dois tipos de distribuição de probabilidade:
•1. Distribuições Contínuas: Quando a variável que está sendo medida é
expressa em uma escala contínua, como no caso de uma característica
dimensional.
•2. Distribuições Discretas: Quando a variável que está sendo medida só
pode assumir certos valores, como por exemplo os valores inteiros: 0, 1,
2, etc.
4.2 Conceitos de distribuição de probabilidade
•No caso de distribuições discretas, a probabilidade de que a variável X
assuma um valor específico xo é dada por: P(X = xo ) = P( xo )
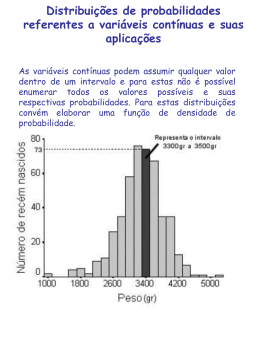
•No caso de variáveis contínuas, as probabilidades são especificadas em
termos de intervalos, pois a probabilidade associada a um número
específico é zero.
Pa  X  b  a f ( x) dx
b
4.3 Distribuição de probabilidade: Uniforme discreta
1) Distribuição Uniforme Discreta
•
•
Suponha que X seja uma variável aleatória discreta uniforme nos inteiros
consecutivos a, a+1, a+2,...,b para a ≤b.
1
f ( x) 
(b  a  1)
ba
E( X )   
2
2 1


b

a

1
V (X )   2 
12

b  a  12  1
12
4.3 Distribuição de probabilidade: Uniforme discreta
Continuação da Distribuição Uniforme Discreta
•
•
Exemplo: A variável aleatória X com distribuição Uniforme discreta denota
o número das 48 linhas telefônicas que estão em uso em um certo tempo.
Considere que X seja uma variável aleatória discreta uniforme com um
faixa de 0 a 48. Calcule a E(X) e V(X).
b  a 48  0

 24
2
2

b  a  12  1 48  0  12  1
2
V (X )   

 14,14
12
12
E( X )   
4.3 Distribuição de probabilidade: Binomial
2) Distribuição Binomial
•A distribuição binomial é adequada para descrever situações em que os
resultados de uma variável aleatória podem ser agrupados em apenas
duas classes ou categorias.
•As categorias devem ser mutuamente excludentes, de forma que não
haja dúvidas na classificação do resultado da variável nas categorias e
coletivamente exaustivas, de forma que não seja possível nenhum outro
resultado diferente das categorias.
•Por exemplo, um produto manufaturado pode ser classificado como
perfeito ou defeituoso, a resposta de um questionário pode ser verdadeira
ou falsa, as chamadas telefônicas podem ser locais ou interurbanas.
4.3 Distribuição de probabilidade: Binomial
•Mesmo variáveis contínuas podem ser divididas em duas categorias, como por exemplo,
a velocidade de um automóvel pode ser classificada como dentro ou fora do limite legal.
•Geralmente, denomina-se as duas categorias como sucesso ou falha. Como as duas
categorias são mutuamente excludentes e coletivamente exaustivas:
P
(
s
u
c
e
s
s
o
)

P
(
f
a
l
h
a
)

1
•Conseqüentemente, sabendo-se que, por exemplo, a probabilidade de sucesso é
P(sucesso) = 0,6, a probabilidade de falha é P(falha) = 1-0,6 = 0,4.
•Condições de aplicação:
• são feitas n repetições do experimento, onde n é uma constante;
• há apenas dois resultados possíveis em cada repetição, denominados sucesso
e falha
• a probabilidade de sucesso (p) e de falha (1- p) permanecem constante em
todas as repetições;
• as repetições são independentes, ou seja, o resultado de uma repetição não é
influenciado por outros resultados.
4.3 Distribuição de probabilidade: Binomial
•Seja um processo composto de uma seqüência de n observações
independentes com probabilidade de sucesso constante igual a p, a
distribuição do número de sucessos seguirá o modelo Binomial:
•
n x
n x
P
(
x
)

p
(
1

p
)
x
•
x = 0,1,....,n
 
•onde   representa o número de combinações de n objetos tomados x
n
x
de cada vez, calculado como:
xn   x!(nn! x)!
4.3 Distribuição de probabilidade: Binomial
•Os parâmetros da distribuição Binomial são n e p.
•A média e a variância são calculadas como:
•
 = np
•
2 = np(1 - p)
•A distribuição Binomial é usada com freqüência no controle de qualidade
quando a amostragem é feita sobre uma população infinita ou muito
grande.
•Nas aplicações de controle da qualidade, x em geral representa o número
de defeituosos observados em uma amostra de n itens.
4.3 Distribuição de probabilidade: Binomial
•Por exemplo, se p = 0,10 e n = 15, a probabilidade de obter x itens não
conformes é calculada usando a equação da Binomial. Por exemplo, para
x=1
 115   1!(1515! 1)!  15


1
51
1
5

1
P
(
1
)

x
0
,
1
0
x
(
1

0
,
1
0
)

1
5

0
,
1
0
x
0
,
2
3

0
,
3
4
1
4.3 Distribuição de probabilidade: Binomial
Resumo da Distribuição Binomial
•
Um experimento aleatório é chamado de experimento binomial, se satisfaça as seguintes
condições:
a) O experimento deve comportar um número fixo de tentativas;
b) As tentativas sejam independentes (o resultado de qualquer tentativa não afeta as
probabilidades das outras tentativas);
c) Cada tentativa resulte em somente dois resultados possíveis classificados em duas
categorias (sucesso e falha);
d) A probabilidade de um sucesso de cada tentativa, denotada por p, permaneça
constante.
•
Notação: S e F (sucesso e falha) denotam as duas categorias possíveis de todas
tentativas; p e q denotam as probabilidades de S e F, respectivamente, assim,
P(S)=p
P(F) = 1-p = q
n é o número fixo de tentativas
X denota um número específico de sucessos em n tentativas, podendo ser qualquer
inteiro entre 0 e n inclusive.
p denota a probabilidade de sucesso em uma das n tentativas e q denota a probabilidade
de falha em uma das n tentativas.
P(X) denota a probabilidade de obter exatamente x sucessos em n tentativas.
•
•
•
•
•
•
4.3 Distribuição de probabilidade: Binomial
Continuação Distribuição Binomial
•
P( X  k ) 
n!
pk .qnk , para k  0, 1, 2, ..., n
(n  k )!k!
•
•
•
•
n=número de tentativas
x=número de sucessos em n tentativas
p=probabilidade de sucesso em qualquer tentativa
q=probabilidade de falha em qualquer tentativa
•
Exemplo: Aplicando a fórmula da probabilidade binomial, determine a probabilidade de
obter 3 estudantes canhotos em uma turma de 15 estudantes, dado que 10% da
população são canhotos. Isto é determine a P(X=3), se n=15, p=0,1 e q=0,9.
P( X  3) 
15!
15.14.13.12!
0,13.0,9153 
0,001.0,282429  0,129
(15  3)!3!
12!3!
4.3 Distribuição de probabilidade: Poisson
3) Distribuição de Poisson
•A distribuição de Poisson é adequada para descrever situações onde existe
uma probabilidade de ocorrência em um campo ou intervalo contínuo,
geralmente tempo ou área.
•Por exemplo, o no de acidentes por mês, no de defeitos por metro quadrado, no
de clientes atendidos por hora.
•Nota-se que a variável aleatória é discreta (número de ocorrência), no entanto a
unidade de medida é contínua (tempo, área).
•Além disso, as falhas não são contáveis, pois não é possível contar o número
de acidentes que não ocorreram, nem tampouco o número de defeitos que não
ocorreram.
4.3 Distribuição de probabilidade: Poisson
•Condições de aplicação:
• o número de ocorrências durante qualquer intervalo depende
somente da extensão do intervalo;
• as ocorrências ocorrem independentemente, ou seja, um excesso
ou falta de ocorrências em algum intervalo não exerce efeito sobre
o número de ocorrências em outro intervalo;
• a possibilidade de duas ou mais ocorrências acontecerem em um
pequeno intervalo é muito pequena quando comparada à de uma
única ocorrência.
4.3 Distribuição de probabilidade: Poisson
•A distribuição de Poissson fica completamente caracterizada por um único
parâmetro  que representa a taxa média de ocorrência por unidade de
medida.
•A equação para calcular a probabilidade de x ocorrências é dada por:
• P( x ) 
e
 x

x = 0, 1, ...,n
x!
•A média e a variância da distribuição de Poisson são:
•
=
•
² = ²
•A aplicação típica da distribuição de Poisson no controle da qualidade é
como um modelo para o número de defeitos (não-conformidades) que
ocorre por unidade de produto (por m2, por volume ou por tempo, etc.).
Distribuição de Poisson
•O número de defeitos de pintura segue uma distribuição de Poisson
com  = 2.
•Então, a probabilidade que uma peça apresente mais de 4 defeitos de
pintura virá dada por:
e 2 24
1  PX  4  1  
 1  0,945  0,055  5,5%
4!
x 0
4
4.3 Distribuição de probabilidade: Poisson
Resumo Distribuição de Poisson
•
Dado um intervalo de números reais, suponha que as contagens ocorram
através do intervalo. Se o intervalo puder ser dividido em subintervalos com
comprimentos suficientemente pequenos tal que
1) A probabilidade de mais de uma contagem em um subintervalo seja zero.
2) A probabilidade de uma contagem em um subintervalo seja a mesma para
todos os subintervalos e proporcional ao comprimento do subintervalo e
3) A contagem em cada subintervalo seja independente de outros
subintervalos.
Então o experimento aleatória será chamado de processo de Poisson.
• λ é o número médio de contagens no intervalo para λ >0;
• A função de distribuição de probabilidades de X dada por
•
•
e x
f ( x) 
, x  0,1,2,...
x!
A média e a variância de X serão:
2
2
•  E( X )   e   V ( X )  

4.3 Distribuição de probabilidade: Poisson
Continuação de Distribuição de Poisson
•
Exemplo: Para o caso do fio delgado de cobre, suponha que o número de falhas siga a
distribuição de Poisson, com uma média de 2,3 falhas por milímetro. Determine a
probabilidade de existir exatamente 2 falhas em 1 milímetro de fio. Designe por X o
número de filhas em 1 milímetro de fio. Então, E(X)=2,3 falhas e
•
•
•
•
•
•
e2,3 2,32
P( X  2) 
 0,265
2!
Determine a probabilidade de 10 falhas em 5 milímetros de fio. Seja X o número de
falhas em 5 milímetros de fio. Então X tem uma distribuição de Poisson com
E(X)=5 . 2,3 = 11,5 falhas
e11,511,510
P( X  10) 
 0,113
10!
Determine a probabilidade de existir, no mínimo,uma falha em 2 milímetros de fio.
Seja X o número de falhas em 2 milímetros de fio. Então X tem uma distribuição de
Poisson com
E(X)=2. 2,3=4,6 falhas
e4,6 4,60
P( X  1)  1  P( X  0)  1 
 0,9899
0!
4.3 Distribuição de probabilidade: Hipergeométrica
•Considere o problema básico de inspeção por amostragem, em que
observamos uma amostra de n itens de um lote com N itens, sendo r
defeituosos. Avaliamos o número X de itens defeituosos na amostra. A
variável aleatória X aparenta ser binomial, mas só é realmente binomial se:
– A seleção da amostra for aleatória (para garantir a mesma probabilidade
p de sair item defeituoso em todos os ensaios);
– Com reposição (para garantir independência entre ensaios).
4.3 Distribuição de probabilidade: Hipergeométrica
•A segunda condição não costuma ser satisfeita na prática. Se a
amostragem for aleatória, mas sem reposição, a distribuição de X é
conhecida como hipergeométrica de parâmetros N, n e r.
•A função de probabilidade de X é expressa por:
•
•
r   N r 
   

x n  x 

P( x) 
N
 
n 
x = 0,1,....,min(r,n)
4.3 Distribuição de probabilidade: Hipergeométrica
•A média e a variância são calculadas como:
•
•
  n p
N n
  n  p  (1  p) 
N 1
2
Continuação da Distribuição Hipergeométrica
Qual a probabilidade de ganhar na Mega-Sena ao jogar 7 números entre os valores de 1 a 60?
Qual a probabilidade de ganhar na quina, na quadra ao jogar os 7 números?
•
•
Uma série de 60 números que variam de 1 a 60
6 números são classificados como sucessos
•
N-k = 60-6 = 54 classificados como falhas
•
Uma amostra de tamanho 7 é selecionada ao acaso, sem reposição, a partir de 60
objetos, em que 6 ≤60 e 7 ≤60.
•
Designe por X a variável aleatória que representa o número de sucessos na amostra.
Calcule P(X=6)
•
Então X tem uma distribuição hipergeométrica
 7  60  7 
 

6
6

6

P( X  6)   
 60 
 
6
 7  53 
7! 53!
  
7
1
 6  0  
6!.1! 0!.53!


60.59.58.57.56.55.54! 50.063.860 7.151.980
 60 
 
(6.5.4.3.2.1).54!
6
 7  60  7 
 

5
6

5

P( X  5)   
 60 
 
6
 7  60  7 
 

4
6

4

P( X  4)   
 60 
 
6
 7  53 
7.6.5! 53.52!
  
1.113
1
 5  1  
5!.2.1 1!.52!


60.59.58.57.56.55.54! 50.063.860 44.981
 60 
 
(6.5.4.3.2.1).54!
6
 7  53 
7.6.5.4! 53.52.51!
  
4
2
35.1378
48.230
1
   
4!3.2.1 2!.51!



60.59.58.57.56.55.54! 50.063.860 50.063.860 1.038
 60 
 
(6.5.4.3.2.1).54!
6
4.3 Distribuição de probabilidade: Hipergeométrica
Continuação de Distribuição Hipergeométrica
Exemplo: Uma batelada de peças contém 100 peças de um fornecedor local de
tubos e 200 peças de um fornecedor de tubos de um estado vizinho. Se quatro
peças forem selecionadas ao acaso e sem reposição, qual será a probabilidade
de que elas sejam todas provenientes do fornecedor local?
• Designe por X o número de peças na amostra do fornecedor local.
• Então X tem distribuição hipergeométrica e a probabilidade requerida é
P(X=4)
•
•
100  300  100 



4
4

4


P( X  4)  
 300 


4


100  200 
100! 200!



 4  0   4!.96! 0!.200!  0,0119
300!
 300 


4!.296!
 4 
Qual é a probabilidade de que duas ou mais peças na amostra sejam
provenientes do fornecedor local?
100  200  100  200  100  200 


 

 


2
2
3
1
4
0





  0,298  0,098  0,0119  0,408
P( X  2)  
 300 
 300 
 300 






4
4
4






4.3 Distribuição de probabilidade: Hipergeométrica
Resumo da Distribuição Hipergeométrica
•
Uma série de N objetos contém
• k objetos classificados como sucessos
• N-k objetos classificados como falhas
• Uma amostra de tamanho n objetos é selecionada ao acaso, sem
reposição, a partir de N objetos, em que k ≤N e n ≤N.
• Designe por X a variável aleatória que representa o número de sucessos
na amostra. Então X tem uma distribuição hipergeométrica
•
 K  N  K 
 

x nx 
f ( x)   
, x  max0, n  K  N  a m in{K,n}
N
 
n
 N n

 N 1 
  E( X )  np e  2  V ( X )  np(1  p)
4.3 Distribuição de probabilidade: Hipergeométrica
Continuação de Distribuição Hipergeométrica
Exemplo: Uma batelada de peças contém 100 peças de um fornecedor local de
tubos e 200 peças de um fornecedor de tubos de um estado vizinho. Se quatro
peças forem selecionadas ao acaso e sem reposição, qual será a probabilidade
de que elas sejam todas provenientes do fornecedor local?
• Designe por X o número de peças na amostra do fornecedor local.
• Então X tem distribuição hipergeométrica e a probabilidade requerida é
P(X=4)
•
•
100  300  100 



4
4

4


P( X  4)  
 300 


4


100  200 
100! 200!



 4  0   4!.96! 0!.200!  0,0119
300!
 300 


4!.296!
 4 
Qual é a probabilidade de que duas ou mais peças na amostra sejam
provenientes do fornecedor local?
100  200  100  200  100  200 


 

 


2
2
3
1
4
0





  0,298  0,098  0,0119  0,408
P( X  2)  
 300 
 300 
 300 






4
4
4






4.4 Distribuição de probabilidade: Normal
•A distribuição Normal é a mais importante das distribuições estatísticas, tanto
na teoria como na prática:
– Representa a distribuição de freqüência de muitos fenômenos naturais;
– Serve como aproximação da distribuição Binomial, quando n é grande;
– As médias e as proporções de grandes amostras seguem a distribuição
Normal (Teorema do Limite Central).
•A distribuição Normal é em forma de sino, unimodal, simétrica em relação à
sua média e tende cada vez mais ao eixo horizontal à medida que se afasta da
média.
•Ou seja, teoricamente os valores da variável aleatória podem variar de - a
+.
•A área abaixo da curva Normal representa 100% de probabilidade associada a
uma variável.
•A probabilidade de uma variável aleatória tomar um valor entre dois pontos
quaisquer é igual à área compreendida entre esses dois pontos.
4.4 Distribuição de probabilidade: Normal
•A área total abaixo da curva é considerada como 100%. Isto é, a área total
abaixo da curva é 1.
área=1
área=0,5 área=0,5
99,73%
95,44%
68,26%
•Percentuais da
distribuição Normal:
2 7 .6 2 7 .8
28
2 8 .2 2 8 .4 2 8 .6 2 8 .8
-1
-2
-3
29
+1
+2
+3
2 9 .2
4.4 Distribuição de probabilidade: Normal
•A distribuição Normal fica completamente caracterizada por dois
parâmetros: a média e o desvio-padrão.
•Ou seja, diferentes médias e desvio-padrões originam curvas normais
distintas, como se pode visualizar nos exemplos contidos na tabela abaixo
onde há amostras provenientes de distribuições com média e desviospadrões distintos.
Distribuições Normal
f(x)
A
B
C
x
a) da distribuição A para B muda a tendência central, mas a
variabilidade é constante;
b) da distribuição A para C muda a variabilidade, mas a tendência
central é constante;
c) da distribuição B para C muda a tendência central e a variabilidade.
4.4 Distribuição de probabilidade: Normal
•Uma conseqüência importante do fato de uma distribuição Normal ser completamente
caracterizada por sua média e desvio-padrão é que a área sob a curva entre um ponto
qualquer e a média é função somente do número de desvios-padrões que o ponto está
distante da média.
•Como existem uma infinidade de distribuições normais (uma para cada média e desviopadrão), transformamos a unidade estudada seja ela qual for (peso, espessura, tempo,
etc.) na unidade Z, que indica o número de desvios-padrão a contar da média.
•Dessa forma, o cálculo de probabilidades (área sob a curva) pode ser realizado através de
uma distribuição Normal padronizada, onde o parâmetro é a variável reduzida Z.
•A distribuição Normal pode ser representada por uma equação matemática dada por:
f ( x) 
1
 2
1  x   2
 

e 2  
4.4 Distribuição de probabilidade: Normal
•A distribuição Normal acumulada é obtida calculando a probabilidade de X
ser menor que um dado valor x:
P( X  x )  F (x )  
x

f ( x) dx
•A solução está apresentada em tabelas da distribuição Normal padronizada
onde se entra com a variável reduzida Z (número de desvios-padrões
distantes da média) e encontra-se F(Z) ou vice-versa.
x 

PX  x  P Z 
  F (Z )  Tabelado
 

4.4 Distribuição de probabilidade: Normal
•A variável reduzida mede a magnitude do desvio em relação à média, em
unidades de desvio padrão.
• Z = 1,5 significa uma observação está desviada 1,5 desvios padrão para
cima da média.
•A variável reduzida é muito útil para comparar distribuições e detectar
dados atípicos.
•Dados são considerados atípicos quando Z > 3.
XX
Z
S
4.4 Distribuição de probabilidade: Normal
•Para sabermos o valor da probabilidade, utilizamos a tabela da
distribuição Normal. Essa tabela nos fornece a área acumulada até o
valor de Z
Área=0,84
1,0
0,84
0,0
Z=1
4.4 Distribuição de probabilidade: Normal
•As áreas correspondentes as probabilidades da distribuição normal padrão
estão tabeladas.
Z
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
1.0
1.1
1.2
1.3
1.4
0.8413
0.8643
0.8849
0.9032
0.9192
0.8438
0.8665
0.8869
0.9049
0.9207
0.8461
0.8686
0.8888
0.9066
0.9222
0.8485
0.8708
0.8907
0.9082
0.9236
0.8508
0.8729
0.8925
0.9099
0.9251
0.8531
0.8749
0.8944
0.9115
0.9265
0.8554
0.8770
0.8962
0.9131
0.9278
0.8577
0.8790
0.8980
0.9147
0.9292
0.8599
0.8810
0.8997
0.9162
0.9306
0.8621
0.8830
0.9015
0.9177
0.9319
Probabilidade de ocorrência de valores abaixo de Z
4.4 Distribuição de probabilidade: Normal
•O cálculo da variável reduzida Z faz uma transformação dos valores reais
em valores codificados.
•Essa transformação é feita descontando-se a média para eliminar o efeito
de localização (tendência central) e dividindo-se pelo desvio-padrão para
eliminar o efeito de escala (variabilidade).
•Uma vez calculada a variável reduzida Z, consulta-se a tabela Normal
padronizada para identificar a probabilidade acumulada à esquerda de Z,
ou seja, a probabilidade de ocorrerem valores menores ou iguais a um
certo valor de Z consultado.
4.4 Distribuição de probabilidade: Normal
• Exemplo 1: Suponha que o peso de um rolo de arame seja normalmente
distribuído com média 100 e desvio-padrão 10. Então o peso está em
torno de 100 a uma distância as vezes maior, as vezes menor que 10.
Z
x 

= Z
1
11
00
1
1
0
0
• Queremos saber qual a probabilidade que um rolo, pego ao acaso da
produção, possuir peso menor ou igual a 110:
P( x <110) = P( Z < 1) =
0,8413
4.4 Distribuição de probabilidade: Normal
•
Se quiséssemos saber a probabilidade do peso do rolo ser maior que
111,6, iniciamos calculando o valor de Z:
111,6 100
Z
1,16
10
•
Encontramos o valor de probabilidade 0,8770.
•
P( Z > 1,16) = 1 - P(Z < 1,16) = 1 - 0,8770 = 0,123
4.4 Distribuição de probabilidade: Normal
•Da mesma forma, se quiséssemos a probabilidade do peso estar entre 120 e
130, teríamos que fazer o seguinte raciocínio:
•P(120 < X < 130) = P(X <130) – P(X < 120) =
• P(Z< (130-100)/10) – P(Z< (120-100)/10) = P(Z<3)-P(Z<2)=
•0,9987 – 0,9772 = 0,0215
•ou seja, 2,15% de chance de um rolo pesar entre 120 e 130
4.4 Distribuição de probabilidade: Normal
•Exemplo 2: A resistência à tração do papel usado em sacolas de supermercado é uma característica de qualidade importante.
•Sabe-se que essa resistência segue um modelo Normal com média 40 psi e
desvio padrão 2 psi.
•Se a especificação estabelece que a resistência deve ser maior que 35 psi,
qual a probabilidade que uma sacola produzida com este material satisfaça a
especificação?




P
X

3
5

1

P
X

3
5
35  40 

PX  35 P  Z 
  PZ  2,5
2 

4.4 Distribuição de probabilidade: Normal
4.4 Distribuição de probabilidade: Normal
•Exemplo 3: O diâmetro do eixo principal de um disco rígido segue a
distribuição Normal com média 25,08 in e desvio padrão 0,05 in.
•Se as especificações para esse eixo são 25,00  0,15 in, determine o
percentual de unidades produzidas em conformidades com as especificações.






P
2
4
,
8
5

x

2
5
,
1
5

P
x

2
5
,
1
5

P
x

2
4
,
8
5

25,15  25,08 

24,85  25,08 
 P Z 

P
Z




0
,
05
0
,
05









P
Z

1
,
4
0

P
Z


4
,
6
0

0
,
9
1
9
2

0
,
0
0
0
0

0
,
9
1
9
2
•ou seja, 91,92% dentro das especificações(área cinza) e 8,08% fora das
especificações.
4.4 Distribuição de probabilidade: Normal
Exemplo anterior
LEI
x
LES
25,08
25,15
=0,05
24,85
4.4 Distribuição de probabilidade: Normal
•Exemplo 4: No exemplo anterior tem-se cerca de 8% de unidades nãoconformes, e essas unidades são invariavelmente do tipo “eixo muito largo”.
•Recalcule o percentual de unidades conformes se o processo estivesse
centrado em 25,00.

25,15  25,00 

24,85  25,00 
P Z 
  PZ 

0
,
05
0
,
05







P
Z

3
,
0

P
Z


3
,
0

0
,
9
9
8
7

0
,
0
0
1
3
5

0
,
9
9
7
3
4.4 Distribuição de probabilidade: Normal
•Exemplo 5: Suponha que
P{ X > x} = 0,05.
Encontre um valor limite x, tal que
X
N
(85
;9).
x  85 

P{ X  x}  1  P{X  x}  1  P  Z 
  0,05
9 

x  85 

P Z 
  0,95
9 

Assim,
x  85
1,645 
;
9
x  99,805