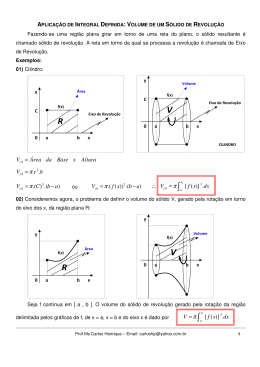
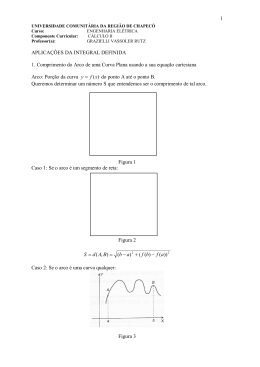
VOLUMES DE SÓLIDOS DE REVOLUÇÃO
Definição: Seja y = f (x) uma função real de variável real contínua em [a, b].
O volume V do sólido de revolução gerado pela rotação da região limitada
pelos gráficos de y = f ( x) , de x=a, de x=b e do eixo dos xx é dado por
b
V = π ∫ [ f ( x)]2 dx .
a
Definição: Seja x = f ( y ) uma função real de variável real contínua em [c, d ].
O volume V do sólido de revolução gerado pela rotação da região limitada
pelos gráficos de x = f ( y ) , de y=c, de y=d e do eixo dos yy é dado por
d
V = π ∫ [ f ( y )]2 dy .
c
Definição: Seja y = f (x) e y = g (x) funções reais de variável real contínuas
em [a, b], com f ( x) ≥ g ( x) ≥ 0 . O volume V do sólido de revolução gerado
pela rotação em torno do eixo dos xx da região limitada pelos gráficos de
y = f (x) , de y = g (x) , de x=a e de x=b é dado por
b
V = π∫
a
{[ f ( x)]2 − [g ( x)]2 }dx .
Definição: Seja x = f ( y ) e x = g ( y ) funções reais de variável real contínuas
em [c, d ], com f ( y ) ≥ g ( y ) ≥ 0 . O volume V do sólido de revolução gerado
pela rotação em torno do eixo dos yy da região limitada pelos gráficos de
x = f ( y ) , de x = g ( y ) , de y=c, de y=d é dado por
d
V = π∫
{[ f ( y)]2 − [g ( y)]2 }dy .
c
Exemplos:
a) A região do plano limitada pelos gráficos das funções y = x , y = 2 x e
y = x 2 roda em torno do eixo dos xx. Determine a medida do volume do
sólido gerado.
b) Utilizando integrais definidos, prove que o volume de uma esfera de raio r é
4
dado por V = πr 3 .
3
c) Determine o volume do sólido de revolução, gerado pela rotação da região
limitada pelos gráficos de y = x 2 e y = 2 , em torno do eixo dos yy.
d) Calcule o volume do sólido de revolução, gerado pela rotação em torno do
eixo dos yy, da região limitada por y = x , y = 2 e x = 0 .
e) Utilizando integrais definidos, prove que o volume de um cilindro circular
recto de altura h e raio r é dado por V = πr 2 h .