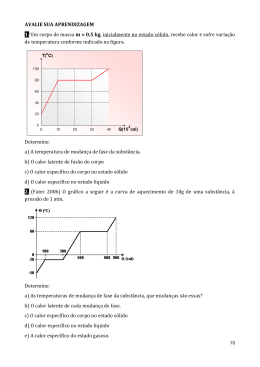
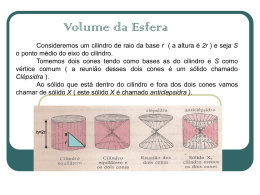
Aplicações de integração
Cálculo 2– Prof. Aline Paliga
Áreas entre curvas
Nós já definimos e calculamos áreas de regiões que estão sob os gráficos
de funções. Aqui nós estamos usando integrais para encontrar áreas de
regiões entre os gráficos de duas funções.
Considere a região S que está entre duas curvas y=f(x) e y=g(x) e entre as
retas verticais x=a e x=b, onde f e g são funções contínuas e f(x)≥g(x)
para todo x em [a,b].
S  ( x, y) / a  x  b, g ( x)  y  f ( x)
Assim como fizemos em aula passada, dividimos S em n faixas de larguras
iguais e então aproximamos a i-ésima faixa por um retângulo com base Δx
*
*
e f  xi   g  xi  . A soma de Riemann é portanto uma aproximação que nós
intuitivamente
pensamos da área de S.
n
  f  x   g  x  x
i 1
*
i
*
i
Esta aproximação parece melhorar
quando n   . Portanto nós definimos
a área A de S como o valor do limite da
soma das áreas destes retângulos
aproximadores:
A  lim   f  xi*   g  xi*   x
n
n 
i 1
A área A da região limitada pelas curvas é então:
A    f  x   g  x   dx
a
b
Notamos que se g(x)=0, S é a região sob o gráfico de f, e nossa definição
acima é reduzida à definição anteriormente estudada.
Se f e g forem positivas:
A  [área sob y  f ( x)]  [área sob y  g ( x)]
=  f  x  dx 
b
a
 g  x  dx
b
a
   f  x   g  x   dx
a
b
EXEMPLO 1:
Encontre a área da região limitada por cima
Por y=ex e por baixo por y=x, e limitada pelos
lados por x=0 e x=1.
RESOLUÇÃO:
1
1
1
0
0
0
A   (e x  x)dx   e x dx   xdx 
1
 x2 
 12 02 
1
0
 e       e  e     
0
 2 0
2 2
1
3
 e  1   e  u.a.
2
2
x 1
EXEMPLO 2:
Encontre a área da região entre as parábolas y=x2 e y=2x-x2 .
RESOLUÇÃO:
Nós primeiro encontramos os pontos de
intersecção das parábolas resolvendo suas
equações simultaneamente.
x2  2x  x2
A   (2 x  x 2 )   x 2   dx    2 x  2 x 2  dx
0
0
1
2x  2x
2
x2  x  0
x( x  1)  0  x  0 e x  1
x  0  y  0 I1 (0,0)
x 1 y 1
I 2 (1,1)
1
 2   x  x 2  dx  2  xdx  2 x 2 dx
1
1
1
0
0
0
1
1
 x2 
 x3 
 12 02   13 03 
    2    2    2  
 2 0
 3 0
2 2 3 3
2 1
 1   u.a.
3 3
Algumas regiões são mais bem tratadas considerando x como uma função
de y. Se uma região é limitada por curvas com equações x=f(y), x=g(y),
y=c e y=d, onde f e g são contínuas e f(y)≥g(y) para c≤y≤d, então sua
área é:
A    f  y   g  y   dy
c
d
EXEMPLO 3:
Encontre a área limitada pela reta y=x-1 e pela parábola y2=2x+6.
RESOLUÇÃO:
Colocando x como função de y nas duas
equações:
y  x 1  x  y  1
y2  2x  6  y2  6  2x
y2  6
x
2
y2
x
3
2
Depois encontramos os pontos de intersecção da parábola e da
reta resolvendo suas equações simultaneamente.
y2
y 1 
3
2
y2  6
y 1 
2
2( y  1)  y 2  6
2 y  2  y2  6
y2  2 y  8  0
(2)  (2) 2  4.1.(8)
y
2.1
26
y
 y  4 e y  2
2
y  2  x  y  1  2  1  1
I1 (-1,-2)
y  4  x  y 1  4 1  5
I 2 (5,4)
4 

 y2

1

A   ( y  1)    3   dy     y 2  y  4  dy
2
2
 2

 2


4
4
1 4
   y 2 dy   ydy  4 dy
2
2
2 2
4
4
4
 y2 
1  y3 
4
        4  y 2 
2  3  2  2  2
1  43  2 
  
2  3
3
  42  2 2 
 
  4  4  (2) 
2
2
 

1  64  8   16 4 
  
  4 6 

2 3
3   2 2 
3
1  72  12 
        24  12  6  24  18u.a.
2 3   2 
Volumes
Na tentativa de encontrar o volume de um sólido nós nos deparamos com
o mesmo tipo de problema para calcular áreas.
Começando com um sólido simples chamado cilindro, que é limitado por
uma região plana B1, chamada base, e a região B2 congruente em um plano
paralelo. O cilindro consiste em todos os pontos nos segmentos de retas
perpendiculares à base que unem B1 e B2. Se á área da base é A e a altura
(distância entre B1 e B2) é h, então o volume é: V  Ah
Para um sólido S que não é um cilindro, nós primeiro “cortamos” S em
pedaços e aproximamos cada pedaço por um cilindro. Chegamos ao
volume exato de S através de um processo de limite quando o número de
partes se torna grande. Pense em fatiar S com uma faca através de x e
calcular a área dessa fatia. A área A(x) varia quando x aumenta de a a b.
seção transversal
Vamos dividir S em n fatias de larguras iguais Δx usando os planos Px1,
Px2,...Se escolhermos pontos de amostragem x*i em [xi-1, xi], podemos
aproximar a i-ésima fatia Si por um cilindro com área de base A(x*i ) com
“altura” Δx .
V  S   A( x* )x
i
i
Adicionando os volumes destas fatias, nós obtemos uma aproximação
para o volume total:
n
V   A( xi* )x
i 1
Esta aproximação parece melhorar quando n   . Pense em tornar as
fatias cada vez mais finas. Portanto, definimos o volume como o limite
destas somas quando n  
. Mas reconhecemos o limite da soma de
Riemann como a integral definida, e assim temos o seguinte definição.
DEFINIÇÃO DE VOLUME
Seja S um sólido que está entre x=a e x=b. Se a área da seção
transversal de S no plano Px, passando por x e perpendicular ao eixo x,
é A(x), onde A é uma função contínua, então o volume de S é:
n
b
i 1
a
V  lim  A( xi* )x   A( x)dx
n 
EXEMPLO 1:
Mostre que o volume de uma esfera de raio r é:
4
V   r3
3
RESOLUÇÃO:
Se colocarmos a esfera de tal maneira que o seu
centro esteja na origem, então o plano Px intercepta
a esfera em um círculo cujo raio (pelo teorema de
Pitágoras) é y  r 2  x2 .
Então a área da seção transversal é:
A( x)   y  
2

r x
2
2

2
   r 2  x2 
Usando a definição de volume com a=-r e b=r, nós temos:
V   A( x)dx     r 2  x 2 dx
r
r
r
r
V     r 2  x 2 dx   r 2  dx    x 2 dx 
r
r
  r 2  x  r
r
r
r
r
r
3
3



r
 x3 


r
2
      r  r  (r )     

3
3
3


 r
r
 r3 
2
4
  r  2r     2   2 r 3   r 3   r 3u.v.
3
3
 3
2
Pela soma de Riemann:
com 5 discos
com 10 discos
com 20 discos
EXEMPLO 2:
Encontre o volume do sólido obtido pela rotação ao redor do eixo
x da região sob a curva y  x de 0 a 1.
RESOLUÇÃO:
Se fizermos a rotação ao redor do eixo x, obteremos o sólido
mostrado acima e se fatiarmos através do ponto x, obtemos um
disco com raio x . A área desta seção transversal é:
A( x)  
 x
2
x
O sólido está entre x=0 e x=1; assim, o seu volume é:
1
 x2 
12 
V   A( x)dx    xdx       
0
0
2 2
 2 0
1
1
EXEMPLO 3:
Encontre o volume do sólido obtido pela rotação da região
limitada por y  x3 , y=8 e x=0
ao redor de y.
RESOLUÇÃO:
Como a região é girada ao redor do eixo y, faz sentido
fatiar o sólido perpendicularmente ao eixo y e portanto
Integrar em relação a y. Se nós fatiarmos a uma altura
y, obteremos um disco circular com raio x onde :
x 3 y
Então a área da seção transversal é:
A( y)   x  
2
 
3
y
2
 y
2
3
Como o sólido está entre y=0 e y=8, seu volume é:
8
 y 53 
8
8
2
 
V   A( y )dy    y 3 dy   
0
0
5 
 3 0
3
=
5
3.5
5
3

3

3 5 3
96
y 3  
83
23 
2 
32 
u.v.
  0 5
5
5
5
5
5
8
EXEMPLO 4:
A região ℜ limitada pelas curvas y=x e y=x2 é girada ao redor do
eixo x. Encontre o volume do sólido resultante:
A( x)    x     x 2    ( x 2  x 4 )
2
2
Portanto temos:
arruela (anel)
1
 x3 x5 
13 15  2
2
4
V   A( x)dx    ( x  x )dx           
u.v.
0
0
 3 5 0
 3 5  15
1
1
Os sólidos dos exemplos 1-4 são chamados de sólidos de revolução,
porque são obtidos pela rotação de uma região ao redor de um eixo. Então
em geral, calculamos o volume de um sólido de revolução usando a
fórmula básica da definição:
b
V   A( x)dx
a
d
ou V  c A( y)dy
e encontramos a A(x) ou A(y) por uma das seguintes maneiras:
Se a seção transversal for um disco (exemplo 1 a 3), nós encontramos
o raio do disco (em termos de x ou y) e usamos:
A   (raio)2
Se a seção for uma arruela (exemplo 4), encontramos o raio interno
rint e o raio externo rext e calculamos a área da arruela subtraindo a área do
disco interno da área do disco externo:
A   (raio externo)2   (raio interno)2