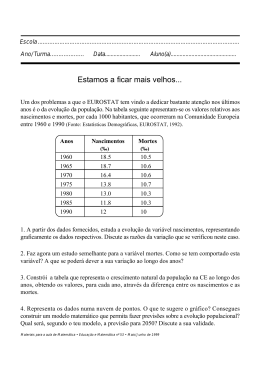
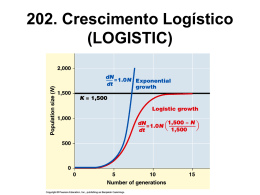
319. População Mundial
(PEOPLE)
O número de pessoas no mundo é o balanço
entre reprodução e mortalidade.
A reprodução por pessoa é afetada pelo
produto dos recursos econômicos por pessoa
e o número de pessoas, onde os recursos
econômicos são avaliados em unidades
emergéticas que incluem recursos ambienteis
e urbanos.
A mortalidade aumenta por doenças e diminui
por recursos econômicos usados para
cuidados com a saúde. PEOPLE é um modelo
que combina esses fatores (Odum e Scott,
1983).
Conforme
os
países
desenvolvem
economicamente a emergia por pessoa
gradualmente declina como as taxas de
natalidade.
Em outras palavras este modelo tem
construída dentro dele a hipótese que a
reprodução da população de uma maneira ou
de outra é diminuída conforme o número de
pessoas aumenta em relação aos recursos.
F
Nonrenewable
Fuels
K0
Renewable J
Resources
L1
R
K1
K2
K3
XXX
X
A
Economic
Assets
K4
K6
L0
:
N
Population
X
1-K9*A
K7
K8
X
-
K5
F= K0*R*F*N*A
R= J/(1+K1*F*N*A+K2*A)
A= K3*R*F*N*A+K4*R*A-K5*A-K6*A-L0*N2*(1-K9*A)-L0*N*(1-K9*A)
N= L1*(A/N)*N-K7*N*(1-K9*A)-K8*N2*(1-K9*A)
Explicação do diagrama e do programa
A esquerda da produção do diagrama de
recursos econômicos é gerada pela interação
do fluxo de recursos renováveis remanescentes
sem uso R reversas de recursos não-renováveis
F retorno de investimentos de recursos
econômicos A e retorno de investimentos da
população N.
Os recursos renováveis disponíveis são os
remanescentes R da entrada J ainda não usada
(Veja
modelo
II-2-Renew)
para
mais
explicações das limitações de constantes fontes
renováveis.
Um fluxo de produção, K3*R*F*N*A, opera
somente quando ainda há combustíveis nãorenováveis disponíveis: outro K4*R*A, se torna
importante somente quando terminam.
A quantidade de recursos econômicos A é um
balanço entre os fluxos produtivos e os fluxos
de saída.
O fluxos de saída incluem a depreciação K5*A,
os
recursos
econômicos
usados
para
desenvolver a população K6*(A/N)*N, os
recursos econômicos usados para saúde e
remédios regulares L0*(1-K9*A) e aqueles
usados para doenças epidêmicas L0*N*N*(1K9*A).
A população N é o balanço entre nascimentos e
mortes. A taxa de natalidade L1*(A/N)*N é
diretamente proporcional aos recursos.
Dois caminhos de mortalidade incluem mortes
regulares e mortes de doenças epidêmicas.
Mortalidade regular K7*N*(1-K9*A) está em
proporção a população N, mas diminui em
relação aos recursos econômicos usados nos
cuidados a saúde (1-K9*A).
A mortalidade epidêmica aumenta em
proporção ao quadrado da população mas
diminui em proporção aqueles recursos usados
nos cuidados a saúde e remédios (1-K9*A).
Um quadrado da população N*N, é apropriado
porque epidemias se espalham quando as
pessoas estão em excesso em proporção as
interações
da
população
que
é
matematicamente o quadrado do número.
A população N se modifica conforme o balanço
entre nascimentos e mortes.
A taxa de nascimentos L1*(A/N)*N é
diretamente proporcional aos bens da
população (A).
18000
16000
14000
12000
10000
8000
6000
4000
2000
0
0
50
100
150
200
N: população
A: bens da economia
F: recursos não renováveis
http://www.unicamp.br/fea/ortega/ModSim/people/people Mi.xls
O programa foi calibrado com valores de 1980.
Na Tabela IV-19a estão os dados usados para
calibrar os coeficientes. Quando o programa é
executado ele gera o gráfico mostrado na
Figura IV-19b.
Como os combustíveis não-renováveis são
usados os recursos econômicos chegam a um
máximo e começam a diminuir. Não muitos
anos depois a população estagna e diminui
rapidamente resultante de menor taxa de
natalidade e maior taxa de mortalidade.
A simulação da população mostra que os
recursos por pessoa durante o crescimento
são maiores que aquelas durante o período
de declínio. Entretanto mais tarde com a
diminuição da população os recursos por
pessoa são razoavelmente bons.
Em um senso esse modelo é otimista ao dizer
que um padrão de vida razoável é possível
em tempos de menor energia fornecendo
níveis de população ajustados para estar em
proporção aos recursos disponíveis ao uso.
Experimentos "E se"
1. Se o tanque de combustíveis fósseis F é
estabelecido a zero o modelo ilustra a
população humana a crescer em energias
renováveis somente. Como o gráfico se
diferenciará do original? Por que?
2. O que você mudaria para demonstrar os
resultados do aumento dos cuidados médicos
(aumente K9)? Como isto muda a população a
longo prazo?
3. Como o gráfico mudaria se em 250 anos a taxa
de natalidade fosse 90% menor - qual seria as
mudanças no futuro imediato e a longo prazo?
(Adicione 515 se T = 250 THEN L1 = 0.0001)
Explique também a diferença entre o gráfico dos
combustíveis.
4. Se uma epidemia de uma doença como a AIDS
piorar como isso mudaria as previsões da
população? Aumente K8 dez vezes e execute a
simulação. então faça as coisas piores também
corte os cuidados médicos a zero.
http://www.unicamp.br/fea/ortega/ModSim/people/people-319.html
COMPUTER MINIMODELS AND SIMULATION EXERCISES FOR
SCIENCE AND SOCIAL STUDIES
Howard T. Odum* and Elisabeth C. Odum+
* Dept. of Environmental Engineering Sciences, UF
+ Santa Fe Community College, Gainesville
Center for Environmental Policy, 424 Black Hall
University of Florida, Gainesville, FL, 32611
Copyright 1994
Autorização concedida gentilmente pelos autores para
publicação na Internet
Laboratório de Engenharia Ecológica e Informática Aplicada - LEIA Unicamp
Enrique Ortega
Mileine Furlanetti de Lima Zanghetin
Liana Barbudo Carrasco
Campinas, SP, 20 de julho de 2007