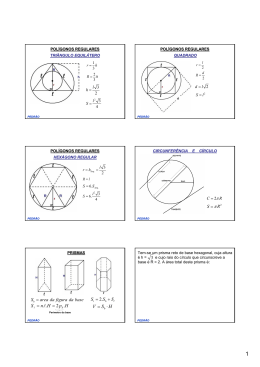
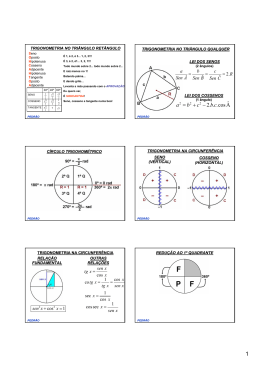
POLÍGONOS REGULARES
POLÍGONOS REGULARES
TRIÂNGULO EQUILÁTERO
QUADRADO
l
2
d
R=
2
1
r= h
3
2
R= h
3
h=
S=
r=
d =l 2
l 3
2
l
2
S = l2
3
4
PEDRÃO
PEDRÃO
POLÍGONOS REGULARES
CIRCUNFERÊNCIA
E
CÍRCULO
HEXÁGONO REGULAR
r = h∆eq. =
l 3
2
R=l
S = 6.S ∆eq.
S = 6.
l2 3
4
C = 2π R
S = π R2
PEDRÃO
PEDRÃO
Uma pirâmide quadrangular regular de 13cm de altura
tem aresta lateral medindo 15cm. A área da base dessa
2
pirâmide, em cm , é:
PIRÂMIDES
Sb = area da figura da base
S l = n.
PEDRÃO
l.a p
2
Sl = Pb ⋅ ap
Semiperímetro da base
Apótema da
pirâmide
S t = Sb + Sl
1
V = .Sb .H
3
PEDRÃO
1
Uma barraca de acampamento tem a forma de uma
pirâmide com 1m de altura, cuja base é um quadrado
com 2m de lado. A quantidade de lona usada nas
faces laterais da barraca é, em metros quadrados:
A figura abaixo representa uma torre, na forma de uma
pirâmide regular de base quadrada, na qual foi
construída uma plataforma, a 60metros de altura,
paralela à base. Se os lados da base e da plataforma
medem, respectivamente, 18m e 10m, a altura da
torre, em metros, é:
PEDRÃO
PEDRÃO
PIRÂMIDES
CONES
PIRÂMIDES
CONES
CONES
Sb = area da figura da base
da
S l = π .R.g
Sl = Pb ⋅ ap Apótema
pirâmide
Semiperímetro
da base
CONE EQUILÁTERO
St = Sb + Sl
360º ~ 2πg ~ πg²
α ~ 2πR ~ setor
1
V = .Sb .H
3
360º ~ 2πg ~ πg²
α ~ 2πR ~ setor
PEDRÃO
PEDRÃO
Um cone circular reto tem altura de 8cm e raio da base
medindo 6cm. Qual é, em centímetros quadrados, sua
área lateral?
Um reservatório de água com a forma e um cone
circular reto tem 8m de altura e, sua base, 3m de raio.
Se a água ocupa 40% da capacidade total do
reservatório, o volume de água nele contido é:
PEDRÃO
PEDRÃO
2
Em uma lanchonete, um casal de namorados resolve
dividir uma taça de milk shake com as dimensões
mostradas no desenho. Se um deles beber sozinho
até a metade da altura do copo, quanto do volume
total, em porcentagem, terá bebido?
PEDRÃO
PEDRÃO
Uma superfície esférica, de raio 13cm, é cortada por
um plano situado a uma distância de 12cm do centro
da superfície esférica, determinando uma
circunferência. O raio dessa circunferência, em cm, é:
ESFERA
R2 = r 2 + d 2
S = 4π R 2
4
V = π R3
3
Planificando a superfície lateral de um cone, obtém-se o
setor circular da figura, de centro O e raio 18 cm . O
valor inteiro mais próximo da altura desse cone é:
FUSO
360º ~ 4π R
α ~ S fuso
CUNHA
2
4
360º ~ π R3
3
α ~ Vcunha
PEDRÃO
PEDRÃO
A área de um círculo máximo de uma esfera vale
2
81πdm . O volume dessa esfera é igual a:
Um observador colocado no centro de uma esfera de
raio 5 m vê o arco AB sob um ângulo α de 72º, como
mostra a figura. Isso significa que a área do fuso
esférico determinado por α é
PEDRÃO
PEDRÃO
3