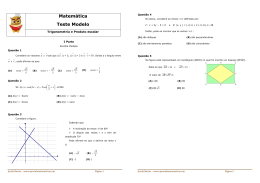
4. Considere num referencial o.n. Oxyz, a esfera definida pela condição x 2 + y 2 + z 2 ≤ 25 .
Matemática
Teste Modelo
A intersecção desta esfera com o plano de equação z=4 é um círculo de área:
(A) 9π
(B) 16π
(C) 25π
(D) 36π
Geometria - 10º ano
I Parte
1. A figura representa um paralelogramo dividido em doze paralelogramos
5. Considere os vectores u (2,−3) e v( x − 3, x + 7) .O valor de x para que os vectores
geometricamente iguais.
Qual das relações seguintes é correcta?
sejam colineares é:
(A) 2
(A) FH + PL = FM
2
MF = BG
3
(C) DI + IM = 0
(B) -1
(C) 5
(
(B) −
(D) -10
II Parte
)
1. Considere, no referencial o.n. O, e 1 , e 2 , os pontos S(-2,3) e T(1,2) e o vector u (2,4 ) .
1.1 Escreva uma equação vectorial da recta r, que contém S e tem a direcção de u .
1.2 Verifique se C(0,1) é ponto da recta ST.
(D) GN + GH = GM
2. Qual das condições seguintes define, em referencial o.n. Oxyz, uma recta paralela ao
1.3 Escreva um vector
eixo Oz?
1.4 Escreva uma equação da circunferência de centro no ponto médio de [ST] e de raio
(A)
(x, y, z ) = (1,0,0) + k (1,1,0) , k ∈ ℜ
(B)
(C)
(x, y, z ) = (1,1,0) + k (0,0,1) , k ∈ ℜ
(x, y, z ) = (1,1,0) + k (1,0,0) , k ∈ ℜ
(D)
x colinear com u e de norma 6 5 .
|| u ||.
2. Na figura estão representados, em referencial o.n. Oxy:
• os pontos A e D, pertencentes ao eixo Oy
• o ponto C, pertencente ao eixo Ox
(x, y, z ) = (0,0,1) + k (1,1,0) , k ∈ ℜ
• a circunferência de centro na origem
3. Qual das seguintes regiões do plano é definida pela condição
(x − 3)2 + ( y + 1)2 > 9 ∨ x < 3 ∨ y > − 1 ?
do referencial e raio 3, que contém
os pontos A, C e D
• a recta BD, que contém o ponto C
• a recta AB, paralela ao eixo Ox
O ponto B tem coordenadas (6,3)
Estão assinaladas na figura duas regiões: uma, tracejada, no primeiro quadrante e
outra, sombreada, no quarto quadrante.
2.1 Escreva as equações reduzidas das rectas AB e BD.
2.2 Mostre que uma equação da mediatriz do segmento [BC] é y = − x + 6
2.3 Defina, por meio de uma condição, a região sombreada, incluindo a fronteira.
2.4 Determine a área da região tracejada. Apresente o resultado arredondado às
centésimas.
Josefa Bastos – www.aprendematematica.com
Página 1
Josefa Bastos – www.aprendematematica.com
Página 2
3. Na figura está representado, em referencial o.n. Oxyz, um sólido que pode ser
decomposto num cubo e numa pirâmide quadrangular regular. A origem do referencial é
Cotações
....................( 5 x 10 pontos )....................
50 pontos
II Parte
1.
1.1
1.2
1.3
1.4
2.
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
150 pontos
46 pontos
pontos
pontos
pontos
pontos
48 pontos
2.1
2.2
2.3
2.4
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
...................................................................
I Parte
um dos vértices do cubo, o vértice P pertence
ao eixo Ox e o vértice R pertence ao eixo Oy.
Os vértices da base da pirâmide
são os pontos médios dos lados do quadrado
[OPQR].
O ponto Q tem coordenadas (2,2,0).
O volume do sólido é igual a 10.
3.1 Indique as coordenadas de:
i)
A + AC
ii)
TU − VU
3.
3.1
i)
ii)
3.2
3.3
3.4
3.5
3.2 Escreva uma equação vectorial da recta
PQ.
3.3 Determine o volume do cubo [OPQRSTUV]. Qual é o volume da pirâmide?
3.4 Determine a cota do ponto E.
3.5 Determine uma equação da superfície esférica que tem centro no ponto T e que
contém o ponto C.
10
12
12
12
12
12
12
12
pontos
pontos
pontos
pontos
46 pontos
12 pontos
4 pontos
8 pontos
6 pontos
8 pontos
10 pontos
10 pontos
4.
...................................................................
10 pontos
Total
...................................................................
200 pontos
4. Na figura está representado um triângulo [ABC]. Os pontos D e E são os pontos médios
dos lados [AB] e [BC], respectivamente.
Utilizando cálculo vectorial, prove que as rectas AC e DE
são paralelas.
Bom Trabalho!
Josefa Bastos
Josefa Bastos – www.aprendematematica.com
Página 3
Josefa Bastos – www.aprendematematica.com
Página 4