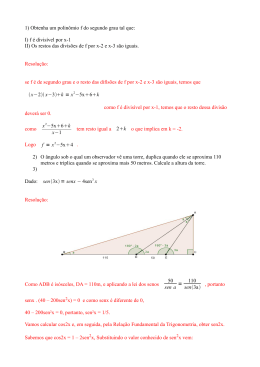
Respostas da Aula 6 do SIM
1)
11
0
0
 11 . 30 = 330 .
6
2) Dividindo 1320 por 360 sobram 2400. Fazendo M = tg 2400 = tg 600 = 3 .
3) Fazendo a regra
x=
135 27 3
.


180
36
4
1800 está para π
1350 está para x
4) Sabendo que cos 1350 = 
2
2
2
3 2
, então calculando a expressão: 3.
.
2
 2
2
2
2
2
5) Como o seno varia de – 1 até 1 calculando na função obtemos 1 + 4. ( -1 ) = - 3 e
1 + 4.1 = 5.
6) log ( tg 2250) = log 1 = 0.
4
+ cos2x = 1. Ao tirar mmc 4 + 9cos2x = 9. Logo
9
5
5
cos2x = e, ao calcular, temos cosx =
.
9
3
7) sen2x + cos2x = 1 substituindo
senx
2 senx
2 cos x
. Como na fórmula sen2x = 2senx.cosx,
, então , 
, senx 
cos x
3 cos x
3
2.2. cos 2 x
podemos escrever sen2x=
. Calculando agora em sen2x + cos2x = 1 substituindo,
3
2
4 cos x
temos:
+ cos2x = 1. Tirando mmc, temos 4 cos2x + 9cos2x = 9. Logo: 13cos2x = 9,
9
4 9 12
então cos2x = 9/13 e que substituído em sen2x temos .  .
3 13 13
8) Fazendo tgx =
9) Como cos2x = 1 – 2sen2x = 1 – 2.
3
1 5
 1  .
36
6 6
10) Substituindo π /3 por 600 na expressão e usando a transformação escrevemos:
senx . cos600 + sen600.cosx – senx . cos600 + sen 600 . cosx = 3 . Simplificando e
calculando, temos:
2 3
cos x  3 . Logo, cos x = 1. Então os valores de x = 0 e x = 2 π.
2
11) Usando a lei dos senos escrevemos:
x
2 4
4

80
2
2
x
80
. Substituindo temos:

0
sen105
sen45 0
.
Calculando temos:
x 2 80( 2  6)

, então , x 2  40( 2  6 ), daí , x  20 2 ( 2  6) , ainda , x  40  40 3,
2
4
substituin do, x  40  40.1,7, então , x  40  68, finalmente , x  108.
12) Primeiramente, usando as razões trigonométricas, cos150 = x / 20, então, x = 20 cos150
e, por sua vez, cos 750 = y / 20. Como cos 750 = sen150, temos: y = 20. sen150.
Também devemos calcular sen750. Então: sen750= sen300 cos450 + sen450 cos300 =
2 3
3 2


2 2
2 2
2 6
.
4
01) A distância entre os prédios é x + y = 20 cos 150 + 20 sen150 = 20( cos150 + sen150);
02) 750 + alfa + 900 = 1800. Logo, alfa = 150;
04) Faça o teorema de Pitágoras: d2 = 202 + 202. Logo d2 = 800 e d < 30 porque d2 deveria
ser 900.
08) sen750 = h / 20. Logo h = 20 sen750. Então h = 20
2 6
. Calculando, então, temos:
4
h = 5( 2  6 ). Devemos somar 2 que é altura do caminhão.
Então 2 + 5( 1, 4 + 1, 4 . 1, 7 ) temos, no cálculo, 2 + 5 ( 1, 4 + 2, 38 ) = 2 + 7 + 11,9 que
resulta em 20,9m. Altura é maior.
16) sen150 = a / 20. Como devemos somar 2 do caminhão teremos a / 2 = 10sen150 + 1.
13) Algumas observações possíveis no gráfico desenhado Im = [-1, 3 ], período p =
7  6
11
5
, -1 ). Fazendo as alternativas de
 
  , ponto de máximo (
,3 ) e mínimo (
6 6
6
12
12
2
trás para frente temos na letra E) não é diretamente porque a fórmula é
onde k é
k
coeficiente do x. O período da letra D é 2 π e o do gráfico é π. A letra C é falsa porque no
gráfico f (π/6 ) = 1 e na lei apresentada f (π/6) = 0. Na letra B o período é p =
2
onde k na
k
frente do x é ½ que substituído na fórmula resulta 4 π. Finalmente a letra A é a correta
porque como o seno varia de -1 até 1 que calculado na lei ficaria 1 – 3 ( -1 ) = 4 maior que
o 3 do gráfico e 1 – 3. 1 = - 2 menor que no gráfico que é -1. Logo a distância entre os
extremos seria maior.
14) Primeiramente, observe o gráfico:
1) Usando Pitágoras no triângulo APR temos x2 = sen2t + ( 1 –
cost)2, então x2 = sen2t + 1 – 2 cost + cos2t. Calculando, temos
x2 = 1 + 1 – 2 cost. Então x = 2  2 cos t . Portanto, falsa.
2) Fazendo A = (base . altura)/2 temos A = (1 . sent)/ 2.
Verdadeira.
3) Usando o mesmo modo do item 2 temos A = (cost . sent)/2.
Como sen(2t) = 2 sent cost, então A = (sent)/4. É verdadeira.