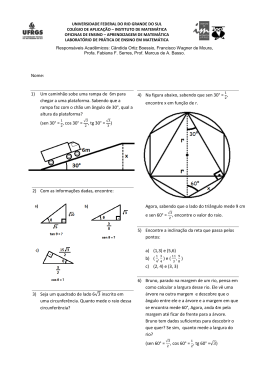
Questão 1
Na figura adiante, åæ = åè = Ø é o lado do decágono
regular inscrito em uma circunferência de raio 1 e centro O.
a) Calcule o valor de Ø.
b) Mostre que cos 36° = (1 + Ë5)/4.
6.28.1
6.18.6
Questão 4
Um relógio foi acertado exatamente ao meio dia.
Determine as horas e minutos que estará marcando esse
relógio após o ponteiro menor ter percorrido um ângulo de
42°.
Questão 2
Um observador, em P, enxerga uma circunferência de
centro O e raio 1 metro sob um ângulo š, conforme mostra
a figura.
6.18.6
Questão 5
Encontre todas as soluções do sistema:
ýsen (x+y) =0
þ
ÿsen (x-y) =0
que satisfaçam 0 ´ x ´ ™ e 0 ´ y ´ ™.
Questão 6
a) Prove que o ponto O se encontra na bissetriz do ângulo
š.
b) Calcule tg(š), dado que a distância de P a O vale 3
metros.
Questão 3
A corda comum de dois círculos que se interceptam é vista
de seus centros sob ângulos de 90° e 60°, respectivamente,
como é mostrado na figura a seguir. Sabendo-se que a
distância entre seus centros é igual a Ë(3)+1, determine os
raios dos círculos.
6.28.8
Sejam a e b os ângulos centrais associados,
respectivamente, aos arcos AN e AM na circunferência
trigonométrica da figura 1 e considere x na figura 2, a
seguir. Determine o valor de y = 15x¥, sabendo que a + b =
™/2.
1
Questão 7
Questão 9
Para calcular a distância entre duas árvores situadas nas
margens opostas de um rio, nos pontos A e B, um
observador que se encontra junto a A afasta-se 20m da
margem, na direção da reta AB, até o ponto C e depois
caminha em linha reta até o ponto D, a 40m de C, do qual
ainda pode ver as árvores.
O valor máximo da função f(x) = 3cos x + 2sen x para x
real é:
a) Ë2/2
b) 3
c) 5Ë2/2
d) Ë13
e) 5
Questão 10
6.28.8
A figura a seguir mostra parte do gráfico da função:
6.28.3
Tendo verificado que os ângulos DCB e BDC medem,
respectivamente, cerca de 15° e 120°, que valor ele
encontrou para a distância entre as árvores, se usou a
aproximação Ë6 = 2,4?
Questão 8
Uma pizza circular será fatiada, a partir do seu centro, em
setores circulares. Se o arco de cada setor medir 0,8
radiano, obtém-se um número máximo N de fatias
idênticas, sobrando, no final, uma fatia menor, que é
indicada na figura por fatia N+1.
6.28.2
a) sen x
b) 2 sen (x/2)
c) 2 sen x
d) 2 sen 2x
e) sen 2x
Questão 11
Dois ângulos distintos, menores que 360°, têm, para seno, o
mesmo valor positivo. A soma desses ângulos é igual a:
a) 45°.
b) 90°.
c) 180°.
d) 270°.
e) 360°.
Questão 12
Considerando ™ = 3,14, o arco da fatia N+1, em radiano, é
a) 0,74.
b) 0,72.
c) 0,68.
d) 0,56.
e) 0,34.
Indique a função trigonométrica f(x) de domínio R; Im =
[-1, 1] e período ™ que é representada, aproximadamente,
pelo gráfico a seguir:
2
Questão 15
6.28.3
Todos os valores de x Æ [™, 2™] que satisfazem
senx.cosx>0 são:
a) ™< x < 5 ™/4
b) 5™/4 < x < ™
c) ™ < x < 3™/2
d) 3™/2 < x < 2™
e) 3™/2 < x < 7™/4
Questão 16
a) y = 1 + cos x.
b) y = 1 - sen x.
c) y = sen (-2x).
d) y = cos (-2x).
e) y = - cos x.
O conjunto solução da equação 2cos£x + cosx - 1 = 0, no
universo U = [0, 2™], é
a) {™/3, ™, 5™/3}
b) {™/6, ™, 5™/6}
c) {™/3, ™/6, ™}
d) {™/6, ™/3, ™, 2™/3, 5™/3}
e) {™/3, 2™/3, ™, 4™/3, 5™/3, 2™}
Questão 13
O período da função y=sen(™Ë2.x) é:
a) Ë2/2.
b) Ë™/2.
c) ™/2.
d) Ë2.
e) 2Ë2.
Questão 17
Seja a Æ [ -™/4, ™/4 ] um número real dado. A solução (x³,
y³) do sistema de equações
Questão 14
No quadrilátero a seguir, BC = CD = 3 cm, AB = 2 cm,
ADC = 60° e ABC = 90°.
6.28.9
ý(sena)x - (cosa)y = - tga
þ
ÿ(cosa)x + (sena)y = - 1
é tal que:
a) x³.y³ = tga
b) x³.y³ = - seca
c) x³.y³ = 0
d) x³.y³ = sen£a
e) x³.y³ = sena
A medida, em cm, do perímetro do quadrilátero é:
a) 11.
b) 12.
c) 13.
d) 14.
e) 15.
3