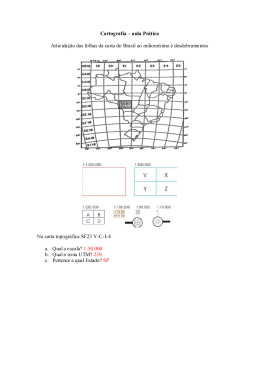
Geometria Analitica – Recordando Pág. 522
Prof. Jefferson Ricart Pezeta
Primeiro de tudo, vamos desenhar o
triângulo proposto pelo enunciado.
O enunciado fornece as coordenadas do
ponto B e do ponto médio entre B e C.
Desta forma, podemos calcular os valores da
coordenada do ponto x usando a fórmula do
ponto médio
 X  X B Y AYB 
M A
,

2
2 

Agora que temos os valores da coordenada
do ponto C, podemos, usando a mesma
fórmula do ponto médio, calcular a
coordenada do ponto A.
Como o enunciado pede o valor do produto
xy, podemos concluir o problema calculando:
a) Para determinar a equação de uma reta,
necessitamos das coordenadas de pelo menos
2 pontos pertencentes à essa reta. Observe no
gráfico que para x valendo -4 temos y valendo
0 e para x=10 temos y=7. Assim, calculando
a determinante, temos:
Alternativa d
Pelos dados do exercício, temos a seguinte
reta:
Para começar vamos desenhar o triângulo
proposto no enunciado.
Sabendo-se que os pontos A, C e B estão
alinhados, podemos determinar a equação
da reta e chamá-la de expressão 1.
Sabendo que AC equivale a três quintos de
AB, temos:
Repare que a mediana do triângulo é um
segmento que intercepta BC ao meio passando
pelo vértice A. Como sabemos os valores das
coordenadas B e C, podemos calcular o valor
de M aplicando-se o conceito de ponto médio.
Ou seja:
Podemos então substituir a expressão 2 na
expressão 1e acharmos valores possíveis
para y:
A reta suporte da mediana passa pelo
segmento suporte da mediana. Como temos
duas coordenadas, M e A, podemos calcular a
equação da reta.
Podemos então definir os valores possíveis
para x:
Iniciaremos o exercício desenhando a reta
proposta pelo exercício.
Para determinar a equação da reta precisamos
de dois pontos. Como o ponto Q é simétrico
do ponto P, temos os valores das duas
coordenadas as quais nos permitirão calcular a
equação da reta solicitada.
Ainda tem dúvidas sobre algum exercício esta página. Poste no blog ou me pergunte em sala
de aula.