PONTO MÉDIO

As coordenadas do ponto médio do segmento ̅̅̅̅, sendo
dadas pela média de cada uma das coordenadas:
(
e
, são
)
Calcule o ponto médio de AB, sendo A(6,-4) e B(2, 8)
(
)
(
)
COMBINAÇÃO LINEAR


Sendo três vetores coplanares, ⃗ , e ⃗⃗ sempre podemos escrever um dos vetores
em função dos outros dois. Assim, se escrevemos ⃗⃗ em função de ⃗ e , dizemos
que escrevemos ⃗⃗ como uma combinação linear de ⃗ e .
Exemplo: Sabendo que os vetores ⃗⃗
,⃗
e
são
coplanares, determine os números  e  tais que ⃗⃗ seja uma combinação linear de
⃗ e . ( ⃗⃗
⃗
).
De onde se obtém o sistema de equações:
{
Fazendo (1) + (2):
Ou seja,
Usando a relação (2):
Ou seja,
.
A relação (3) pode ser usada para verificar a validade da relação:
Ou seja, como a equação (3) resulta em uma igualdade verdadeira, os três vetores são
coplanares.
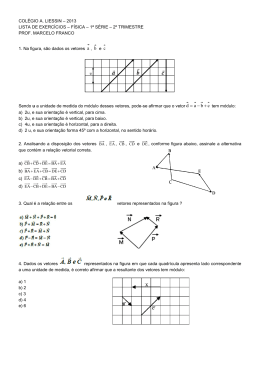
EXERCÍCIOS DE RECAPITULAÇÃO
1. Represente os seguintes vetores graficamente:
a) ⃗
b)
c) ⃗⃗
2. Determine o valor de a, tal que
e
sejam paralelos.
EXERCÍCIOS DE COMBINAÇÃO LINEAR
3. Dados os vetores ⃗⃗
,⃗
e
, determine os
valores de  e  tais que ⃗⃗ seja uma combinação linear de ⃗ e . ( ⃗⃗
4. Dados os vetores ⃗⃗
⃗ e
,⃗
⃗
).
, determine os
valores de  e  tais que ⃗⃗ seja uma combinação linear de ⃗ e . ( ⃗⃗
⃗
).
5. Verifique se os três vetores listados são coplanares ou não. Obs: Se três vetores são
coplanares, então um desses vetores pode ser escrito como uma combinação linear
dos outros dois; do contrário, se não forem coplanares, não há  e  que satisfaça a
relação de combinação linear.
a)  ⃗⃗
b) ⃗⃗
,⃗
,⃗
e
e