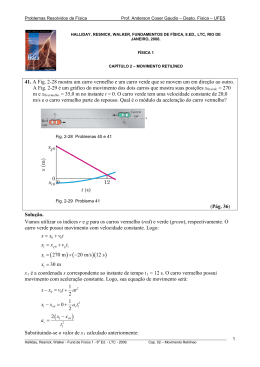
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 4.ED., LTC, RIO DE
JANEIRO, 1996.
FÍSICA 2
CAPÍTULO 18 – ONDAS II
21. Na Fig. 18-25, dois alto-falantes, separados por uma distância de 2,00 m, estão em fase.
Supondo que a amplitude dos sons dos dois seja, de modo aproximado, a mesma na posição do
ouvinte, que está a 3,75 m diretamente à frente de um dos auto-falantes. (a) Para quais
freqüências audíveis (20 - 20.000 Hz) existe um sinal mínimo? (b) Para quais freqüências o som
fica ao máximo?
(Pág. 158)
Solução.
Considere o seguinte esquema:
O
L
A
B
D
(a) O som chegará com sinal mínimo ao ouvinte quando a diferença entre os percursos AO e BO for
igual a (n +1/2) λ, n = 0, 1, 2, etc.
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 18 – Ondas II
1
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
1

d AO − d BO = n +  λ
2

(D
2
+ L2
)
1/ 2
1 v

− L = n+ 
2 f

1
v

=
f n+ 
2  D 2 + L2

(
1

=
f  n +  686 s −1
2

(
)
1/ 2
−L
)
Para que seja audível, a freqüência da onda no ponto O deve ser 20 Hz < f < 20 kHz. Logo:
n=0
f = 343 Hz
Audível
n=1
f = 1.029 Hz
Audível
...
...
...
n = 28
f = 19.551 Hz
Audível
n = 29
f = 20.237 Hz
Inaudível
Portanto, as freqüências audíveis são dadas por:
1

0 ≤ n ≤ 28.
=
f  n +  686 s −1 ,
2

(b) O som chegará com sinal máximo ao ponto O quando:
(
)
d AO − d BO =
nλ ,
(D
2
+ L2
)
1/ 2
n = 0, 1, 2, etc.
−L=
n
v
f
v
f =n
(D + L )
f = n ( 686 s )
2
2
1/ 2
−L
−1
Para que seja audível, a freqüência da onda no ponto O deve ser 20 Hz < f < 20 kHz. Logo:
n=0
f = 0 Hz
Não há onda
n=1
f = 686 Hz
Audível
...
...
...
n = 29
f = 19.894 Hz
Audível
n = 30
f = 20.580 Hz
Inaudível
Portanto, as freqüências audíveis são dadas por:
(
)
f = n 686 s −1 ,
0 ≤ n ≤ 29.
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 18 – Ondas II
2