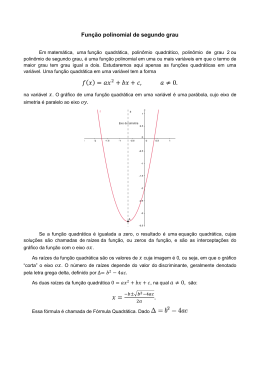
Teoria
ENEM
Prof.: Lucas Dias
FUNÇÃO DO PRIMEIRO GRAU: (AFIM)
RESUMÃO:
f:    f(x) = ax + b com a  0 , onde a é chamado de coeficiente angular e b de coeficiente linear (termo
independente)
Exemplos: a) f(x) = 2x + 1 b) g(x) = -x – 3. Observe que no exemplo a, o valor do coeficiente angular é 2, ou seja,
maior do que zero, logo classificamos a função como sendo crescente. Ao passo que, no exemplo b, o valor do
coeficiente angular é -1, ou seja, menor do que zero, logo classificamos a função como sendo decrescente.
Função linear:
f:    f(x) = ax com a  0 . Ex: f(x) = 2x. Observamos que o termo independente é nulo, logo sua reta passa pela
origem do plano cartesiano.
Função identidade:
f:    f(x) = x. Observamos que a função identidade é um caso particular da função linear, onde a = 1 e b = 0.
Concluímos então, que sua reta passa pela origem do plano e passa também pela bissetriz dos quadrantes
ímpares.
Zero da função: é o valor de x para o qual a função se anula. Geometricamente falando, é onde a reta “corta” o
b
eixo das abscissas. Relação: ax + b = 0, então x = 
a
Estudo do sinal:
FUNÇÃO DO SEGUNDO GRAU: (QUADRÁTICA)
RESUMÃO:
f:    f(x) = ax2 + bx + c onde a  0 , pois, se a = 0 teremos uma função afim, ou seja, f(x) = bx + c. Dizemos
que a, b e c são coeficientes reais.
Zeros da função quadrática:
Denominam-se zeros de uma função quadrática os valores de x que anulam a função, ou seja, que tornam f(x) =
0. Então, seja f(x) = ax2 + bx + c, para determinarmos os zeros da função basta igualarmos a mesma a zero, ou
seja,
ax2 + bx + c = 0. Para encontrarmos as raízes da equação, utilizaremos a fórmula de Bhaskara:
x 
 b   , onde
  b 2  4ac .
2a
Observação:
a) Se  > 0 a equação terá duas raízes reais distintas;
b) Se  = 0 a equação terá duas raízes reais iguais;
c) Se  < 0 a equação não possuirá raízes reais.
Soma e produto dos zeros da função quadrática:
b
c
S 
e P
a
a
Multiplica
Lista 1
ENEM
Teoria
ENEM
Prof.: Lucas Dias
Forma fatorada da função quadrática:
f(x) = a(x – x1)(x – x2) onde x1 e x2 são os zeros da função.
Gráfico da função quadrática:
O gráfico da função quadrática é uma curva aberta chamada de parábola.
Observamos que, sua concavidade é para cima quando a > 0 e para baixo
quando a < 0.
Vértice da parábola:
b

Xv = e yv = 2a
4a
Estudo do sinal:
Multiplica
Lista 1
ENEM