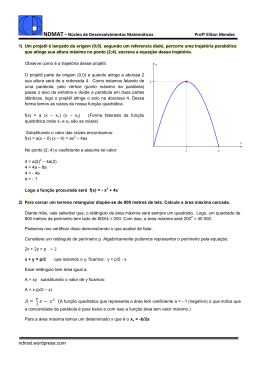
Objetos de Aprendizagem
Função Quadrática
—————————————————————————————————————————–
Função Quadrática - Questões.
—————————————————————————————————————————–
Maria, possui um terreno retangular medindo 25 × 40 metros, sendo 25 metros de frente, onde construiu
uma casa e fez uma plantação de hortaliças, conforme ilustra a figura abaixo.
Entre a casa e a Plantação existe uma área livre de 5 metros de largura. Maria decidiu ampliar a área
construída, aumentando a mesma medida tanto na largura quanto no comprimento da casa, mas mantendo
a mesma área livre entre a casa e a plantação e a mesma distância da frente e da lateral esquerda do terreno.
Para isso, será necessário diminuir a área plantada. Quanto deve ampliar na lateral direita da casa para
que a área construída seja igual a 221 m2 ? Qual é a maior área possível de ser construída?
Para obter um modelo matemático que possibilite a simulação da área construída e a área plantada, a
partir do ambiente computacional apresentado, responda as questões sugeridas.
1. Com o botão direito do mouse selecione a ferramenta <Área>
e, em seguida, clique no rótulo:
(a) Terreno para determinar a área total do terreno;
(b) Casa para determinar a área construída inicialmente;
(c) Novacasa para determinar a área total construída;
(d) Plantação para determinar a área plantada.
2. Com o botão direito do mouse selecione a ferramenta
da medida das áreas.
. Mova o ponto P e observe a variação
3. A seguir, clique na caixa < gráfico da função fab >, para exibir o gráfico na tela. Mova, novamente,
o ponto P e observe o comportamento do gráfico da função fab . Qual é a variável que determina o
comportamento do gráfico? Justifique.
4. O gráfico representa uma função? Qual o seu domínio? Qual é a sua imagem? (Para melhor visualizar
o gráfico ative a ferramenta Reduzir (veja figura) e clique na tela, preferencialmente no ponto (0, 0), o número de vezes
necessário até visualizar todo o gráfico .
ou use uma mudança de escala nos eixos x e y, da seguinte forma: Clique como botão esquerdo do mouse na tela, escolha
a opção <eixoX:eixoY> e, em seguida, 1:5).
5. O gráfica é um segmento de reta? Justifique.
6. Obtenha uma expressão algébrica para a função que representa a área total construída, em função
de s, e denomine-a de g(s).
7. Reinicialize o ambiente computacional, clicando em
no Campo <Entrada> para exibir o seu gráfico.
e digite a função g, substituindo s por x,
8. Uma função f : R → R, definida por f (x) = ax2 +bx+c, onde a, b e c são constantes reais e a 6= 0,
é denominada de função quadrática. A função g é uma função quadrática? Explique.
9. Exiba < gráfico da função fab > e <gráfico da função auxiliar1 >. A partir do <controle deslizante>
que define o parâmetro w, com o auxílio do mouse, arraste w para zero. O que ocorreu com os
gráficos das funções fab e auxiliar1 ?
10. Considerando a área construída, qual o significado do valor 140 assumindo inicialmente pelo parâmetro w?
2
11. Considerando a situação problema, o que representa os valores da função fac ?
12. A função fac é uma função quadrática (com restrição de domínio)? Obtenha uma expressão algébrica para a função fac .
13. Obtenha uma expressão algébrica para a função que representa a área total da plantação, em função
de s, denomine-a de h(s). A função obtida é uma função quadrática? Justifique.
14. Reinicialize o ambiente computacional e digite a expressão obtida para h, substituindo s por x, no
campo <Entrada>, para exibir o gráfico da função obtida, com x real, isto é, ampliando o domínio
da função h para o conjunto dos números reais.
15. Exiba o gráfico da função fap . Qual o domínio e a imagem de fap ? (use a ferramenta Reduzir ou mude
a escala dos eixos). As funções f ap e h, representadas pelos gráficos exibidos na tela, são iguais?
Justifique.
16. Obtenha uma expressão algébrica que represente a área livre do terreno, denomine-a de f t(s). A expressão obtida define um função? Qual o seu domínio? A função obtida é uma função quadrática?
Justifique.
17. Reinicialize o ambiente computacional e digite a expressão obtida, substituindo s por x, no campo
Entrada. O gráfico exibido na tela representa a função que modela matematicamente a área livre
do terreno?
3