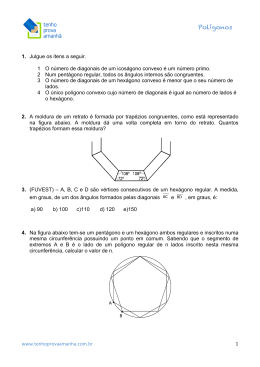
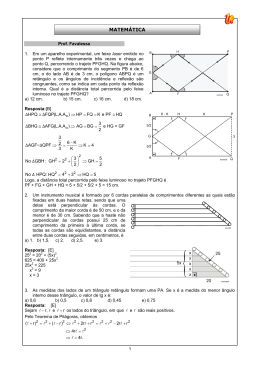
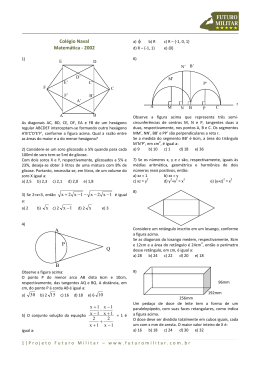
1. A respeito das diagonais de um hexágono regular de lado medindo 1 cm, é correto afirmar-se que
a) são nove, de três comprimentos diferentes, e as menores medem 3 cm.
b) são nove, de dois comprimentos diferentes, e as maiores medem
3 cm.
c) são nove, de dois comprimentos diferentes, e as menores medem
3 cm.
d) são doze, de três comprimentos diferentes, e as maiores medem
e) são doze, de dois comprimentos diferentes, e as menores medem
3 cm.
3 cm.
2. No estudo da distribuição de torres em uma rede de telefonia celular, é comum se encontrar um
modelo no qual as torres de transmissão estão localizadas nos centros de hexágonos regulares,
congruentes, justapostos e inscritos em círculos, como na figura a seguir.
Supondo que, nessa figura, o raio de cada círculo seja igual a 1km, é correto afirmar que a distância d3,8
(entre as torres 3 e 8 ), a distância d3,5 (entre as torres 3 e 5 ) e a distância d5,8 (entre as torres 5 e 8 )
são, respectivamente, em km, iguais à
a) d3,8 2 3, d3,5 3, d5,8 3 2 3.
b) d3,8
4, d3,5
c) d3,8
4, d3,5
3, d5,8
5.
d) d3,8
3 3
, d5,8
2
2 3, d3,5 3, d5,8
e) d3,8
4, d3,5
3 3
, d5,8
2
3 3
.
2
21.
4
9
.
2
TEXTO PARA A PRÓXIMA QUESTÃO:
Arquimedes,candidato a um dos cursos da Faculdade de Engenharia, visitou a PUCRS para colher
informações. Uma das constatações que fez foi a de que existe grande proximidade entre Engenharia e
Matemática.
3. Para uma engrenagem mecânica, deseja-se fazer uma peça de formato hexagonal regular. A distância
entre os lados paralelos é de 1cm, conforme a figura abaixo.
O lado desse hexágono mede ______ cm.
1
3
a)
b)
3
2
c)
3
d)
5
5
e) 1
4. Os pontos A, B, C e D são vértices consecutivos de um polígono regular com 20 diagonais, cujo lado
mede 1. O comprimento do segmento AD é igual a:
a) 2
b) 1
c) 2 2 1
d) 2 2 1
e) 2 2
2
5. Na figura abaixo, O é o centro de uma circunferência que
tangencia a semirreta BA no ponto A e tangencia o segmento
BE no ponto C. Sabendo ainda que BA é paralela à reta OF, que
o segmento EF é perpendicular a OF e que o menor arco da
circunferência com extremidades em A e C mede º 60, podemos
afirmar que o ângulo DÊF mede:
a) 20º
b) 30º
c) 50º
d) 60º
6. Sejam P e Q polígonos regulares. Se P é um hexágono e se o número de diagonais do Q, partindo de
um vértice, é igual ao número total de diagonais de P então a medida de cada um dos ângulos internos de
Qé
a) 144 graus.
b) 150 graus.
c) 156 graus.
d) 162 graus.
7. Na figura a seguir, o pentágono ABCDE, inscrito no círculo, é regular. A soma das medidas dos
ângulos a, b, c, d e e, indicados na figura, é
°
a) 150 .
°
b) 180 .
°
c) 270 .
°
d) 360 .
°
e) 450 .
Gabarito:
Resposta da questão 1:
[C]
6.(6 3)
9.
2
Medida das diagonais maiores: 1 + 1 = 2 cm.
Número de diagonais: d =
Medida das diagonais menores: x.
2
2
2
Na figura: x + 1 = 2
x=
3
são nove, de dois comprimentos diferentes, e as menores medem
3 cm.
Resposta da questão 2:
[D]
d3,8
4.a
4.1. 3
2
2 3
d3,5
1 1 1 3
d5,8
3
2
2
9
2
2
84
4
21
Resposta da questão 3:
[B]
Como o raio r do círculo inscrito no hexágono é a metade da distância entre os lados paralelos, segue
1
cm. Logo, o lado do hexágono regular é dado por
que r
2
1
2
3
3
2
cm.
3
3
Resposta da questão 4:
[B]
Sabendo que o número de diagonais (d) de um polígono regular em função do número de lados (n) é
n (n 3)
n (n 3)
, temos que 20
n2 3n 40 0 n 8.
2
2
Logo, A, B, C e D são vértices consecutivos de um octógono regular, cujo ângulo interno mede
dado por d
180 (n 2)
n
180 (8 2)
8
135 .
De posse desses dados, considere a figura abaixo.
Como os triângulos AB'B e CC 'D são congruentes, basta calcularmos AB', pois BB 'C 'C é retângulo.
Assim, AB'
AB
1
2
2
Por conseguinte,
AD
2 AB ' B 'C'
2
2
2
1
2 1.
Resposta da questão 5:
[B]
o
o
y + 60 = 90 ;
o
o
Logo, y = 30 e z = 60 .
o
Portanto, x + z = 90 = x = 30
o
Resposta da questão 6:
[B]
Diagonais de P:
6.(6 3)
2
Lados de Q: n – 3 = 9
Ângulo interno de Q:
9
n = 12
180(12 2)
= 150 graus
12
Resposta da questão 7:
[B]
2
.
2