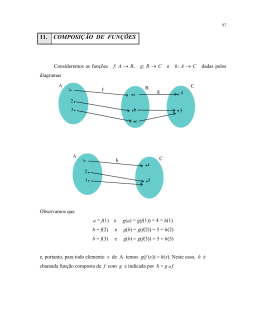
UNIDADE I I
funções
CA P Í T U LO
Banco de questões
2 Noções de função
1(UEL – PR) Uma cadeia de restaurantes estima que
a demanda de arroz, a cada 30 dias, seja de 600 kg.
Desde que começou as atividades, a empresa mantém um estoque mínimo de 50 kg como reserva.
Considerando que todos os dias é consumida a
mesma quantidade de arroz nos restaurantes; que
o estoque geral é reposto a cada 10 dias no começo de cada período e que a função A = A( t ), com
0 ≤ t ≤ 30 expressa a quantidade de arroz em estoque em cada dia t, então a função A é dada por:
3(UFMG – MG) Seja f uma função real, tal que
f ( x + 8 ) = f ( x ) para todo x real.
O gráfico de f para −4 ≤ x ≤ 4 é apresentado
nesta figura:
 200 − 20t, se 0 ≤ t < 10

a)A( t ) =  400 − 20t, se 10 ≤ t < 20
600 − 20t, se 20 ≤ t ≤ 30

 20t + 250, se 0 ≤ t < 10

b)A( t ) =  20t + 450, se 10 ≤ t ≤ 20
20t + 650, se 20 < t ≤ 30

 20t − 200, se 0 ≤ t < 10

c)A( t ) =  20t − 400, se 10 ≤ t ≤ 20
20t − 600, se 20 < t ≤ 30

 7
a)Calcule f   .
 4
b)Calcule f ( 31).
 20t, se 0 ≤ t < 10

d)A( t ) = 20t − 250, se 10 ≤ t ≤ 20
20t − 450, se 20 < t ≤ 30

c)Faça o esboço do gráfico de f para 6 ≤ x ≤ 14.
4(UFV – MG) Seja Ω = { A, B, C, D, E, F, G, H, I, J, K, L,, X, Y , Z },  250 − 20t, se 0 ≤ t < 10

e)A( t ) = 450 − 20t, se 10 ≤ t < 20
650 − 20t, se 20 ≤ t ≤ 30

conjunto das letras do alfabeto brasileiro (incluindo K, W, Y ). Considere Ω 1 um subconjunto
de  e f : Ω → Ω 1 a função definida por f ( A) = 3,
2(Uespi – PI) Analise as afirmativas abaixo para
toda função real.
1.Toda função bijetora admite função inversa.
2.O gráfico de uma função ímpar é simétrico
em relação à origem do sistema de eixos cartesianos.
3.O conjunto domínio de uma função par é simétrico em relação à origem do sistema cartesiano.
Está(ão) correta(s):
a)1 apenas
b)1 e 3 apenas
c)1 e 2 apenas
d)2 e 3 apenas
e)1, 2 e 3
f ( B ) = 27, f (C ) = 243, f ( D) = 2187 e assim por
diante. Suponha, ainda, que f é bijetora e que
f −1 é sua inversa. Calculando
f
−1
(3) f (3 ) f (3 ) f (3 )
−1
23
−1
9
−1
25
e mantendo esta ordem, obtém-se a palavra:
a)A N E L
b)A L G O
c)A L E M
d)A M E I
e)A N I L
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro
5(UFV – MG) Considere f :  →  uma função real,
 cos x
2
1 

1
2 . O
definida por f ( x ) = det sen x


 0
− sen x cos x 
6(UFC – CE) Para cada número real x ≠ 1, define-se
x
f ( x ) por f ( x ) =
. Então, f ( f ( x )) é sempre
x −1
igual a:
a)x
gráfico cartesiano que melhor representa a função f é:
b)− x
( )
c) f ( x )
d) f ( x ) 
e) f x 2
2
a)
7(UFC – CE) Os reais não nulos p e q são tais que a
equação x 2 + px + q = 0 tem raízes ∆ e 1− ∆, sendo
que ∆ denota o discriminante dessa equação.
Assinale a opção que corresponde ao valor de q:
1
7
a)−1
c)
e)
4
8
1
3
b)−
d)
2
16
b)
8(UFPE – PE) O valor da média salarial dos funcioná­
rios de uma empresa, com x anos de trabalhos
prestados, é dada por s ( x) = 100 x + 3 + x + 10 .
Para quan­tos meses trabalhados na empresa a
mé­dia salarial será de R$ 700,00 ?
(
)
9(UFPR – PR) Abaixo estão representados os gráficos das funções f e g.
c)
d)
Sobre esses gráficos, considere as seguintes afir­
mativas:
1.A equação f ( x ) ⋅ g ( x ) = 0 possui quatro so­lu­
ções no intervalo fechado [ −10,10 ].
2.A função y = f ( x ) ⋅ g ( x ) assume apenas va­lo­
res positivos no intervalo aberto ( 0, 3).
3. f ( g ( 0 )) = g ( f ( 0 )).
4.No intervalo fechado [ 3,10 ], a função f é de­
e)
crescente e a função g é crescente.
Assinale a alternativa correta:
a)Somente as afirmativas 1 e 2 são verdadeiras.
b)Somente as afirmativas 1, 2 e 4 são verdadeiras.
c)Somente as afirmativas 3 e 4 são verdadeiras.
d)Somente as afirmativas 1, 3 e 4 são verdadeiras.
e)Somente as afirmativas 2 e 3 são verdadeiras.
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro
10(UFPR – PR) Considere a função f, definida no
conjunto dos números naturais pela expressão
f ( n + 2) = f ( n) + 3, com n ∈, e pelos dados
f ( 0 ) = 10 e f (1) = 5 . É correto afirmar que os va-
lores de f ( 20 ) e f ( 41) são, respectivamente:
a)21 e 65
b)40 e 65
c)40 e 56
d)21 e 42
e)23 e 44
11(UFG – GO) A área da superfície corporal pode
ser calculada aproximadamente pela fórmula de
ph
Mosteller, A =
, em que A é a área em m2 , p
60
é o peso em quilogramas e h a estatura em cm.
Assim sendo, calcule:
a)a área da superfície corporal de uma pessoa
, m de estatura
que pesa 80 kg e tem 18
b)o percentual de aumento da área corporal de
uma pessoa adulta, caso o seu peso altere de
70 kg para 84,7 kg
12(UFG – GO) A seguir é descrito uma brincadeira
popular para se descobrir a idade de alguém.
É pedido a uma pessoa, com idade inferior a 100
anos, que multiplique por dois o número do mês
de seu aniversário, adicione 5 ao resultado e, em
seguida, multiplique por 50 o valor obtido. Depois, ela deve adicionar a própria idade ao número obtido e informar o resultado. Subtraindose 250 desse resultado, obtém-se um número
X, com o qual se descobre facilmente o mês de
nascimento e a idade da pessoa. Nessas condições, se o número do mês de nascimento é N, e
a idade é I,
a)obtenha uma expressão matemática de X em
função de N e de I
b)descubra o valor de N e de I, se o número
obtido pela pessoa for X = 819
13(UFMS – MS) Seja f :  →  uma função real, tal
que f (1) = A, f ( e ) = B e f ( x + y ) = f ( x ) ⋅ f ( y ),
para todo x e y pertencente a . Então, f ( 2 + e )
é igual a:
a) A
b) B
c) A2B
d) AB2
e) A2 − B
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro
Respostas do capítulo 2
1e 2e
 7
27
3a ) f   = −
 4
16
7
b ) f ( 31) =
4
c )
4c
5a
6a
7d
872
9a 10b
11a ) 2 m2
b ) 10%
12a ) X = 100N + I
b ) N = 8, I = 19
13c
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro