Para as 2 questões a seguir use o enunciado:
Pesquisas mostram que, em modalidades que exigem bom condicionamento
aeróbico, o coração do atleta dilata, pois precisa trabalhar com grande volume de
sangue.
Em um esforço rápido e súbito, como um saque no tênis, uma pessoa normal pode
ter o pulso elevado de 70 a 100 batimentos por minuto; para um atleta, pode se
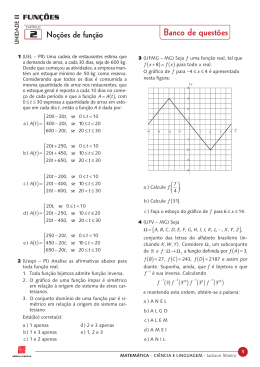
elevar de 60 a 120 bpm, como mostra o gráfico abaixo.
01. A expressão da função f que, a cada t segundos, 0 ≤ t ≤ 4, faz corresponder o
número f(t), de batimentos cardíacos do atleta é
a) f(t) = 15t + 60
b) f(t) = 10t + 80
20t + 60, se 0 ≤ t < 2
10t + 80, se 2 ≤ t ≤ 4
c) f (t ) = 
20t + 60, se 0 ≤ t < 2
15t + 60, se 2 ≤ t ≤ 4
d) f (t ) = 
15t + 60, se 0 ≤ t < 2
10t + 80, se 2 ≤ t ≤ 4
e) f (t ) = 
Resposta: C
1
Para 0 ≤ t < 2
f(t) = ax + b
P(0, 60)
60 = b
Q(2, 100)
100 = 2a + b
100 = 2a + 60
a = 20
f(t) = 20t + 60
Para 2 ≤ t ≤ 4
f(t) = at + b
Q(2, 100)
100 = 2a + b
R(4, 120)
120 = 4a + b
2a + b = 100

4a + b = 120
2a = 20 → a = 10
b = 80
f(t) = 10t + 80
02. Se o aumento dos batimentos cardíacos de uma pessoa normal ocorre de forma
linear, então os números de batimentos cardíacos do atleta e de uma pessoa normal
serão iguais, após quantos segundos do momento do saque?
a) 0,8
b) 0,78
c) 0,75
d) 0,64
e) 0,6
Resposta: A
Para atleta: f(t) = 20t + 60
Para pessoa normal:
f(t) = at + b
P(0, 70)
70 = b
S(4, 100)
100 = 4a + 70
4a = 30
a = 7,5
f(t) = 7,5t + 70
Para que sejam iguais:
2
20t + 60 = 7,5t + 70
12,5t = 10
t = 0,8 s
03. Seja f: R → R uma função definida por f(x) = mx + p. Se f passa pelos pontos
A(0,4) e B(3,0), então f-1 passa pelo ponto
a) (8, -2)
b) (8, 3)
c) (8, -3)
d) (8, 2)
e) (8, 1)
Resposta: C
f(x) = ax + b
A(0, 4)
4=b
B(3, 0)
0 = 3a + 4
-4 = 3a
a = -4/3
f(x) = -4x/3 + 4
− 4x
+4
3
− 4y
x=
+4
3
− 4y
x−4=
3
3 x − 12 = −4 y
3 x − 12
y=
−4
12 − 3 x
f −1 ( x) =
4
12 − 3.8
f −1 (8) =
4
12 − 24 − 12
f −1 (8) =
=
= −3
4
4
P(8,−3)
y=
3
04. Na figura a seguir, tem-se o gráfico de uma reta que representa a quantidade,
medida em mL, de um medicamento que uma pessoa deve tomar em função de seu
peso, dado em kgf, para tratamento de determinada infecção.
O medicamento deverá ser aplicado em seis doses.
Assim, uma pessoa que pesa 85kgf receberá em cada dose:
a) 7 mL
b) 9 mL
c) 8 mL
d) 10 mL
Resposta: B
f(x) = ax + b
A(25,12)
12 = 25a + b
B(65, 40)
40 = 65a + b
4
65a + b = 40

− 25a − b = −12
40a = 28
28 7
=
40 10
b = 12 − 25a
a=
7
10
175
b = 12 −
10
120 − 175 − 55
b=
=
10
10
7
55
f ( x) = x −
10
10
7
55
f (85) = 85 −
10
10
595 55 540
f (85) =
−
=
= 54
10 10 10
54
= 9mL
6
b = 12 − 25
05. Um grande poluente produzido pela queima de combustíveis fósseis é o SO2
(dióxido de enxofre). Uma pesquisa realizada na Noruega e publicada na revista
"Science" em 1972 concluiu que o número (N) de mortes por semana, causadas pela
inalação de SO2, estava relacionado com a concentração média (C), em mg/m3, do
SO2 conforme o gráfico a seguir: os pontos (C, N) dessa relação estão sobre o
segmento de reta da figura.
Com base nos dados apresentados, a relação entre N e C (100 ≤ C ≤ 700) pode ser
dada por:
a) N = 100 - 700 C
b) N = 94 + 0,03 C
5
c) N = 97 + 0,03 C
d) N = 115 - 94 C
e) N = 97 + 600 C
Resposta: B
f(x) = ax + b
A(100, 97):
97 = 100a + b
B(700, 115):
115 = 700a + b
700a + b = 115

− 100a − b = −97
600a = 18
18
3
a=
=
600 100
b = 97 − 100a
3
b = 97 − 100.
100
b = 97 − 3 = 94
3x
f ( x) =
+ 94
100
N = 94 + 0,03C
06. O gráfico representa uma função f que descreve, aproximadamente, o movimento
(em função do tempo t em segundos) por um certo período, de um golfinho que salta
e retorna à água, tendo o eixo das abscissas coincidente com a superfície da água.
6
a) Sabendo que a parte negativa do gráfico de f é constituída por segmentos de
retas, determine a expressão matemática de f nos instantes anteriores à saída do
golfinho da água. Em que instante o golfinho saiu da água?
b) A parte positiva do gráfico de f é formada por parte de uma parábola, dada por:
f(t) = (- 3/4) t2 + 6t - 9.
Determine quantos segundos o golfinho ficou fora da água e a altura máxima, em
metros, atingida no salto.
Resposta:
f(x) = ax + b
a)
A(0, -4)
-4 = b
B(1, -2)
-2 = a + b
-2 = a - 4
a=2
f(x) = 2x – 4
P/ y = 0:
0 = 2x – 4
4 = 2x
x=2
b)
f(t) = (- 3/4) t2 + 6t - 9.
Aplicando Báskara:
t1 = 2 e t2 = 6. O golfinho sai da água em t = 2 e retorna em t = 6. Logo ele fica fora da
água por 4 segundos.
xV =
−b
=
2a
−6
−6
=4
=
 −3 −3
2.

2
 4 
− 3 .4 2
+ 6 .4 − 9
4
yV = −12 + 24 − 9
yV =
yV = 3 metros
07. Considere as funções f e g, ambas com domínio e contradomínio real, dadas por
f(x) = 5x -
2 e g(x) = x2 – 6x + 1, para qualquer x real. A respeito dessas funções,
assinale o que for correto.
01) A imagem de qualquer número racional, pela função f, é um número irracional.
02) A função g possui uma única raiz real.
7
04) Ambas as funções são crescentes no intervalo [0,+∞[ do domínio.
08) O gráfico da função f o g é uma parábola.
16) Ambas as funções possuem inversas.
Resposta: 09
01) f(x) = 5x - 2
f(a) = 5a - 2 , que é irracional
02) ∆ = b2 – 4ac
∆ = (-6)2 – 4.1.1
∆ = 36 – 4 = 32
∆ > 0, logo g tem 2 raízes reais.
04) g(x) não é crescente em todo o intervalo dado.
08) f o g = 5(x2 – 6x + 1) - 2
f o g = 5x2 – 30x + 5 - 2 que é função quadrática. Logo o gráfico é uma parábola.
16) g(x) não possui inversa.
08. Resolvendo a equação real 9x – 3x+1 - 4 = 0, têm-se:
a) x = 0
b) 3x = 4
c) x = 1
d) x = 2
e) 4x = 3
Resposta: B
9x – 3x+1 - 4 = 0
32x – 3x+1 – 4 = 0
Fazendo 3x = y
y2 – 3y – 4 = 0
y1 = 4 e y2 = -1 (não serve)
3x = 4
09. Um barco parte de um porto A com 2x passageiros e passa pelos portos B e C,
deixando em cada um metade dos passageiros presentes no momento de chegada, e
recebendo, em cada um, 2x/2 novos passageiros. Se o barco parte do porto C com 28
passageiros e se N representa o número de passageiros que partiram de A, é correto
afirmar que:
a) N é múltiplo de 7
b) N é múltiplo de 13
c) N é divisor de 50
8
d) N é divisor de 128
e) N é primo
Resposta: D
x
 2x

2

−
−
2
x 
x
 2

+ 2  +  2
+ 22  =
2 x +  −


2
2

 



x
2
x
2x
2 x −1 − 2 2
2x −
+ 22 −
+ 22 =
2
2
x
x
x
2
x −1
x
2
x
2
2 .2 − 2 + 2 .2 − 2 − 2 + 2
=
2
x
x
2x 2x
+ 2 .2 2
2 x + 2 .2 2 −
2 = 2
=
2
2
x
x
x
Fazendo 2 2 = a :
a2
+ 2a
2
= 28
2
a2
+ 2a = 56
2
a 2 + 4a − 128 = 0
a1 .a 2 = −128
log o a1 é múltiplo de 128
10. Determine uma das soluções da equação 10 x
2
−4
=
1
.
1000
Resposta: x1 = 1 e x2 = - 1
1
1000
10 x
2
−4
=
10 x
2
−4
= 10 −3
x 2 − 4 = −3
x2 = 1
x1 = 1 e x 2 = −1
9
11. A inflação anual de um país decresceu no período de sete anos. Esse fenômeno
pode ser representado por uma função exponencial do tipo f(x) = a.bx, conforme o
gráfico a seguir.
Determine a taxa de inflação desse país no quarto ano de declínio.
Resposta: 60
f(x) = a.bx
P/ (0, 960)
960 = a.b0 ⇒ a = 960
P/ (7; 7,5)
7,5 = 960.b7
b7 = 1/27
b=½
f(x) = 960.(½)x
P/ x = 4
f(4) = 960.(½)4
f(4) = 60
12. Ao resolver uma questão, José apresentou o seguinte raciocínio: "Como ¼ > 1/8
tem-se (1/2)2 > (1/2)3 e conclui-se que 2 > 3."
a) Identifique o erro que José cometeu em seu raciocínio, levando-o a essa
conclusão absurda.
b) Sem cometer o mesmo erro que José, determine o menor número m, inteiro e
1
positivo, que satisfaz à inequação  
2
4
m
1
> 
4
m +1
Resposta:
a) Tem-se uma inequação de base a, com 0 < a < 1. Para resolvê-la deve-se inverter
a desigualdade. Assim, (1/2)2 > (1/2)3, então, 2 < 3.
b)
10
1
 
2
4
m
1
> 
4
4
m +1
2 m+ 2
1 m 1
  > 
2
2
4
< 2m + 2
m
4
2m + 2 − > 0
m
2
2 m + 2m − 4
>0
m
m2 + m − 2 > 0
O menor inteiro positivo que satisfaz a inequação é 2.
13. A automedicação é considerada um risco, pois, a utilização desnecessária ou
equivocada de um medicamento pode comprometer a saúde do usuário: substâncias
ingeridas difundem-se pelos líquidos e tecidos do corpo, exercendo efeito benéfico ou
maléfico.
Depois de se administrar determinado medicamento a um grupo de indivíduos,
verificou-se que a concentração (y) de certa substância em seus organismos
alterava-se em função do tempo decorrido (t), de acordo com a expressão y = y0 2 −0,5t
em que y³ é a concentração inicial e t é o tempo em hora. Nessas circunstâncias,
pode-se afirmar que a concentração da substância tornou-se a quarta parte da
concentração inicial após:
a) 1/4 de hora
b) meia hora
c) 1 hora
d) 2 horas
e) 4 horas
Resposta: E
11
y = y 0 2 −0,5t
y0
= y 0 2 − 0 , 5t
4
2 − 2 = 2 − 0 , 5t
−2= −
t
2
t=4
14. Na figura, os gráficos I, II e III referem-se, respectivamente, às funções y = ax, y =
bx e y = cx. Então, está correto afirmar que:
a) 0 < a < b < c
b) 0 < b < c < a
c) a < 0 < b < c
d) 0 < a < c < b
e) a < 0 < c < b
Resposta: D
Pela análise direta das alternativas, percebe-se que a < c < b. Nas funções
exponenciais tem-se sempre a base > 0. Então, 0 < a< c < b.
15. A trajetória de um salto de um golfinho nas proximidades de uma praia, do
instante em que ele saiu da água (t = 0) até o instante em que mergulhou (t = T), foi
descrita por um observador através do seguinte modelo matemático h(t ) = 4t − t.2 0,2t ,
com t em segundos, h(t) em metros e 0 ≤ t ≤ T. O tempo, em segundos, em que o
golfinho esteve fora da água durante este salto foi
a) 1.
b) 2.
12
c) 4.
d) 8.
e) 10.
Resposta: E
0 = 4t − t.2 0, 2t
t 2 0 , 2 t = t .2 2
0,2t = 2
t = 10
16. Suponha que o modelo exponencial y = 363e0,03x, em que x = 0 corresponde ao
ano 2000, x = 1 corresponde ao ano 2001, e assim sucessivamente, e que y é a
população em milhões de habitantes no ano x, seja usado para estimar essa
população com 60 anos ou mais de idade nos países em desenvolvimento entre 2010
e 2050. Desse modo, considerando e0,3 = 1,35, estima-se que a população com 60
anos ou mais estará, em 2030, entre
a) 490 e 510 milhões.
b) 550 e 620 milhões.
c) 780 e 800 milhões.
d) 810 e 860 milhões.
e) 870 e 910 milhões.
Resposta: E
y = 363e0,03x
y = 363e0,03.30
y = 363e0,9
y = 363(e0,3)3
y = 363.1,353
y = 363.2,46
y = 892,98
17. Nos processos industriais, como na indústria de cerâmica, é necessário o uso de
fornos capazes de produzir elevadas temperaturas e, em muitas situações, o tempo
de elevação dessa temperatura deve ser controlado, para garantir a qualidade do
produto final e a economia no processo. Em uma indústria de cerâmica, o forno é
programado para elevar a temperatura ao longo do tempo de acordo com a função
13
7
t + 20, para 0 ≤ t < 100
 5
T (t ) = 
, em que T é o valor da temperatura atingida pelo
2
16
2

t − t + 320, para t ≥ 100
125
5
forno, em graus Celsius, e t é o tempo, em minutos, decorrido desde o instante em
que o forno é ligado. Uma peça deve ser colocada nesse forno quando a temperatura
for 48 °C e retirada quando a temperatura for 200 °C. O tempo de permanência dessa
peça no forno é, em minutos, igual a
a) 100.
b) 108.
c) 128.
d) 130.
e) 150.
Resposta: D
7
T (t ) = t + 20
5
7
48 = t + 20
5
7
28 = t
5
t = 20 min utos
2 2 16
t − t + 320
125
5
2 2 16
t − t + 120 = 0
125
5
2
t
8t
− + 60 = 0
125 5
t 2 − 200t + 7500 = 0
t1 = 150 e t 2 = 50 (não serve)
200 =
Tempo total = 150 – 20 = 130 minutos
18. Sobre a função quadrática f(x) = x2 – mx + (m + 3), onde m ∈ R, assinale o que
for correto.
01) Se m < –2 ou m > 6, f(x) admite duas raízes distintas.
02) Se m = 2, f(x) tem duas raízes iguais.
04) Se m = 4, f(x) tem um ponto de máximo em x = 2.
14
08) Se –2 < m < 6, f(x) não tem raízes reais.
16) Se m < –3, f(x) admite duas raízes distintas e positivas.
Resposta: 09
f(x) = x2 – mx + (m + 3)
Delta: (- m)2 – 4.1.(m + 3)
Delta: m2 – 4m – 12
m1 = - 2 e m 2 = 6
Se m < –2 ou m > 6, f(x) admite duas raízes distintas
Se -2 < m < 6 não admite raízes reais
Se m = -2 ou m = 6 admite 1 raiz real
Se m = 4: f(x) = x2 – 4x + 7
−b
2a
4
xV = = 2
2
xV =
xV = 2 é ponto de mínimo
19. A função quadrática f(x) = ax2 + bx + c é tal que f(0) = 3, f(1) = 4 e f(–1) = 0.
Nessas condições, assinale o que for correto.
01) O gráfico de f(x) é uma parábola com a concavidade voltada para baixo.
02) f(x) não intercepta o eixo x.
04) f(x) > 0 para todo x no intervalo ]–1, 3[.
08) f(x) é decrescente no intervalo [0, ∞[.
16) A imagem de f(x) é { y ∈ R / y ≤ 1 }.
Resposta: 05
f(x) = ax2 + bx + c
f(x) = 3, então c = 3
f(1) = 4, então a + b + 3 = 4
a+b=1
f(-1) = 0, então a – b + 3 = 0
a – b = -3
a + b = 1

 a − b = −3
a = -1
b=2
f(x) = -x2 + 2x + 3
15
y
4
3
2
1
x
−4
−3
−2
−1
1
2
3
4
5
−1
−2
−3
−4
16