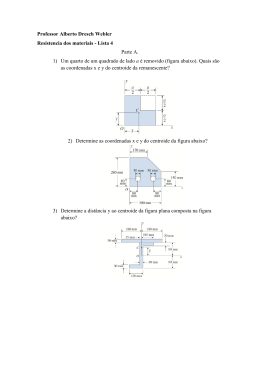
1) Determine o momento de inércia do corpo em relação ao eixo indicado na figura (tracejado).
2) Determine o centróide, o produto de inércia e os momentos de inércia da figura acima em relação aos eixos
ilustrados. As funções ilustradas são F1 (x) = −20.3333 +10.75 ∗ x−0.9166666 ∗ x2 e F2 (x) = 3.5714 +0.00669 ∗
x3
3) Determine os momentos de inércia e o produto de inércia em relação a um sistema de eixos centroidal.
Após, desenho o círculo de Mohr e determine qual deve ser a rotação do sistema de coordenadas para que tenhamos um produto de inércia nulo.
4) Determine o máximo ângulo que a peça pode ter em relação ao eixo X para que seja mantido o equilíbrio
estático. A peça tem uma densidade que varia de acordo com a relação ρ (x′ ) = 7850 + 100 ∗ x′ [Kg/m3]