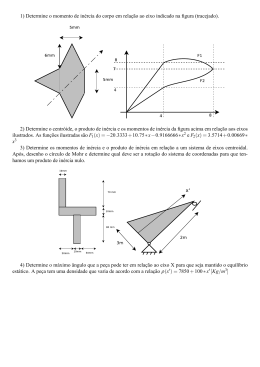
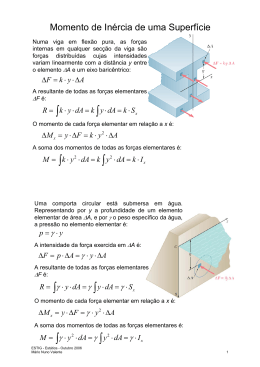
PUC – Goiás
Curso: Engenharia Civil
Disciplina: Mecânica dos Sólidos
Corpo Docente: Geisa Pires
Plano de Aula
Turma:-----------
Data: ------/--------/----------
Leitura obrigatória
Mecânica Vetorial para Engenheiros, 5ª edição revisada, Ferdinand P. Beer, E. Russell Johnston, Jr.
Editora Pearson
CAPÍTULO 9 – Forças Distribuídas: Momento
de Inércia
inercia em relação ao eixo que passa pelo
centróide.
1. Introdução
Na última parte deste capítulo analisaremos a
transformação dos momentos de inércia pela
rotação dos eixos coordenados.
No cap. 5 analisamos vários sistemas de forças
distribuídas sobre superfícies ou sólidos. Os
principais tipos de força que consideramos foram
pesos de placas homogêneas de espessura
uniforme, cargas distribuídas em vigas e forças
hidrostáticas. Em todos os casos considerados, as
forças distribuídas eram proporcionais às áreas ou
volumes elementares a elas associados. A
resultante dessas forças podiam ser obtidas
somando as correspondentes áreas e volumes.
Momentos de Inércia de Superfícies
2. Momento de Segunda Ordem ou Momento
de Inércia de uma Superfície
Na primeira parte deste capítulo consideraremos
forças distribuídas F proporcional ao elemento
de área A na qual elas agem e que variam
linearmente com a distância de A a um certo
eixo, F  kyA .
Na primeira parte deste capítulo consideraremos
forças distribuídas F cujos módulos dependem
da área A do elemento de superfície em que
atuam e da distância desse elemento a um dado
eixo. Mais precisamente, o módulo da força por
unidade de área, F / A , variará linearmente com
a distância ao eixo. Como veremos na próxima
seção, forças desse tipo são encontradas no estudo
da flexão de vigas e em problemas que envolvem
superfícies submersas não-retangulares. Supondo
que as forças elementares estejam distribuídas
sobre uma superfície de área A e que variem
linearmente com a distância y ao eixo x,
verificaremos que, embora o módulo da resultante
R dependa do momento de primeira ordem
Q X   ydA da superfície de área A, a localização
do ponto de aplicação de R depende do momento
de segunda ordem ou momento de inércia,
I X   y 2 dA , da mesma superfície, com relação ao
O módulo da resultante R das forças elementares
F sobre uma seção inteira é
eixo x. Aprenderemos então a calcular os
momentos de inércia de várias superfícies com
relação a eixos x e y dados. Faremos ainda a
utilização do teorema dos eixos paralelos para
determinar o momento de inércia em relação a um
eixo qualquer quando se conhece o momento de
R   kydA  k  ydA
Essa última integral obtida é conhecida como
momento de primeira ordem Qx da seção em
relação ao eixo x. O módulo M do momento fletor
1
deve ser igual à soma dos momentos
M X  yF  ky2 A das forças elementares.
Integrando sobre a seção inteira, obtemos:
relação ao eixo x de uma faixa retangular paralela
ao eixo y, semelhante à representada na figura
abaixo.
M   ky 2 dA  k  y 2 dA
A última integral é conhecida como momento de
segunda ordem ou momento de inércia da seção da
viga em relação ao eixo x e é representada por I X .
Observe que I sempre terá valores positivos.
3. Determinação do Momento de Inércia de
uma Superfície por Integração.
I X   y 2 dA
Assim:
I Y   x 2 dA
dI x 
Exemplo: Determine o momento de inércia de
uma superfície retangular.
1 3
y dx
3
Por outro lado, temos:
dI y  x 2 dA  x 2 ydx
4. Momento Polar de Inércia
Uma integral muito importante em problemas
relativos à torção de eixos cilindricos e em
problemas referentes à rotação de placas é
J 0   r 2 dA
dA  bdy
Onde r é a distância do elemento de área dA ao
pólo O. Essa integral é o momento polar de
inércia.
dI x  y 2 bdy
h
1
I x   by 2 dy  bh 3
3
0
A fórmula que acabamos de deduzir pode ser usada
para determinar o momento de inércia dI x em
2
Exercícios
Determine, por integração direta, o momento de
inércia da superfície sombreada, em relação aos
eixos x e y e o raio de giração para ambos os eixos:
1 – R: I y  3a 3b / 10 I x  b 3 a / 6
Temos ainda:
J 0   r 2 dA   ( x 2  y 2 )dA   y 2 dA   x 2 dA
J 0  I X  IY
5. Raio de Giração de uma Superfície
2–
R: I y  2a 3b / 11
I x  2b 3 a / 51
Consideremos uma superfície de área A, que tem
um momento de inércia Ix em relação ao eixo x.
Imaginemos que concentramos esta área em uma
faixa estreita, paralela ao eixo x. Se a área A, assim
concentrada, deve ter o mesmo momento de inércia
em relação ao eixo x, a faixa deve estar colocada a
uma distância kx desse eixo, definida pela relação
3 – R: I y  2a 3b / 15
I x  2b 3 a / 7
I x  kx A
2
A expressão acima tem um análogo ao eixo y.
A grandeza kx é conhecida como raio de giração.
4 – R: I y  a 3b / 21 I x  b 3 a / 30
3
6. Teorema dos Eixos Paralelos
7. Momentos de Inércia de Superfícies
Compostas
Consideremos o momento de inércia I de uma
superfície de área A em relação a um eixo AA' .
Seja y a distância de um elemento de área dA a
AA' . Escrevemos:
I   y 2 dA
Tracemos agora um eixo BB ' paralelo a AA' , que
passa pelo baricentro C da superfície; esse eixo é
denominado eixo baricêntrico.
Sendo y ' a distância do elemento dA a BB ' ,
temos y  y'd , escrevemos:
I   y 2 dA   ( y ' d ) 2 dA
I   y ' 2 dA  2d  y ' dA  d 2  dA
I  I  Ad 2
4
Exercícios
8. Produto de Inércia
5 – Determine o momento de inércia e o raio de
giração da superfície sombreada em relação ao
eixo x e ao eixo y:
A integral
Pxy   xydA
Obtida multiplicando-se cada elemento dA de uma
superfície A por suas coordenadas x e y e
integrando-se cada elemento dA de uma superfície
A por suas coordenadas x e y e integrando sobre a
superfície é conhecida como produto de inércia da
superfície A em relação aos eixos x e y. Ao
contrário dos momentos de inércia, o produto de
inércia tanto pode ser positivo quanto negativo.
Quando um ou ambos os eixos x e y são eixos de
simetria da superfície A, o produto de inércia é
zero. Isso se deve ao fato de que para cada
elemento de área de coordenada x e y existe um
elemento oposto de coordenada –x e –y.
Evidentemente, a contribuição de cada par de
elementos escolhidos desse modo se cancela
mutuamente, e a integral se reduz a zero.
6 – Determine o momento de inércia e o raio de
giração da superfície sombreada em relação ao
eixo x e ao eixo y:
Deixarei a cargo do aluno a demonstração abaixo
que é um teorema dos eixos paralelos semelhante
àquele estabelecido para calculos de momento de
inércia válido para produto de inércia (Mecânica
Vetorial para Engenheiros, 5ª edição, pag. 636,
PEARSON):
Pxy  Px ' y '  x y A
5
Exercícios
7 – Determine por integração direta o produto de
inércia da superfície dada em relação aos eixos x e
y:
R: a4/8
9. Eixos e Momentos Principais de Inércia
6
7
8
9
10
11
12
Exercício:
Determinar o produto de inercia do triangulo retângulo ilustrado tanto em relação aos eixos x e y
quanto em relação aos eixos baricêntricos paralelos aos eixos x e y.
13
14