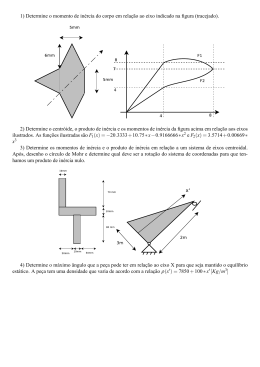
Tensor de inércia
Há outras grandezas associadas à geometria e à massa específica
que é necessário (quando lidarmos com dinâmica) calcular.
São integrais, em volume, de produtos das coordenadas pela massa
específica, que se arrumam no chamado tensor de inércia:
ou,
(onde
é o operador designado como
como produto exterior,
exterior onde cada
elemento do vector é multiplicado por cada elemento do outro vector
gerando-se
se assim uma matriz)
Trata-se
se de um tensor simétrico de 2ª ordem cuja forma matricial é:
- 57 -
As componentes diagonais designam-se
designam se “momentos de inércia” e
tomam valores positivos (trata-se
se de integrais de quadrados das
distâncias).
As componentes não diagonais
são os produtos de inércia. Podem ser <,> ou = 0.
São iguais a 0, em relação a um determinado
terminado par de eixos, quando
um desses eixos é um eixo de simetria do corpo.
No contexto da Dinâmica interessa calcular os momentos e produtos
de inércia “de massas”,
massas” mede-se
se de facto a “inércia”, a “resistência”,
a rotações das massas.
massas Daí que a integração
ração seja feita num elemento
infinitesimal de massa.
No contexto da Resistência de Materiais interessa calcular os
momentos e produtos de inércia “de secções”,
secções” trata--se de uma
propriedade da secção tal como a área.
área. Neste caso a integração é
feita num elemento
mento infinitesimal de área.
- 58 -
Assume, como veremos mais tarde, especial importância a definição
do tensor/matriz de inércia de um corpo rígido em relação a um
ponto O.
Componentes dos vectores de posição e distâncias envolvidas nas
definições dos momentos e dos produtos de inércia:
O momento de inércia de um corpo em relação a um eixo
qualquer é o integral (a soma) dos produtos das massas (dM) das
várias partículas do sistema pelos quadrados das respectivas
distâncias
dλ
ao referido eixo:
- 59 -
Num referencial
ortonormado tem-se:
com as componentes da
diagonal principal a serem os
momentos de inércia em
relação a cada um dos eixos
:
(notar que estes termos são sempre
positivos)
e os simétricos dos termos
não diagonais a serem os
produtos de inércia (em
relação a pares de eixos):
(notar que estes termos não têm
que ser positivos)
3D - Para que todos os
produtos de inércia de um
corpo (em relação a um
referencial ortonormado num
ponto) se anulem basta que
dois planos coordenados
sejam planos de simetria.
- 60 -
Particularização para o caso plano:
No caso plano as expressões para as componentes da matriz de
inércia simplificam-se significativamente:
todos os outros produtos de inércia são nulos.
2D - o produto de inércia de
um corpo (em relação a um
referencial ortonormado
num ponto) é nulo se este
tiver um plano de simetria.
- 61 -
- 62 -
Determinação de momentos de inércia (de massa)
O momento de inércia em relação a um eixo toma a forma:
I = ∫ r 2 dM
M
ou seja:
I = ∫ r 2 ρ ( x, y, z )dV
V
Quando a massa específica é constante é possível simplificar:
I = ρ ∫ r 2 dV = ρ ∫∫∫ r 2 dxdydz
V
V
Particularizando para o termo
I xx = ρ ∫
xf
xi
(∫∫ ( y
A
2
I xx :
)
+ z 2 )dydz dx
Se esse eixo corresponder ao de uma dimensão em relação à qual
a secção transversal A não varie, por exemplo, a situação de uma
barra de secção transversal constante axb e de comprimento L:
- 63 -
então
(
)
I xx = ρL ∫∫ ( y + z )dydz = ρL ∫
I xx =
2
2
A
b/2
∫
a/2
−b / 2 − a / 2
( y 2 + z 2 )dydz
1
ρLab(a 2 + b 2 )
12
Notar que
ρLab
é a massa total da barra, pelo que se poderia
escrever:
I xx = M
1 2
(a + b 2 )
12
Para os momentos segundo os outros eixos o procedimento é
idêntico:
I yy = ρb ∫
L/2
∫
a/2
− L / 2 −a / 2
I yy =
( x 2 + z 2 )dxdz
1
1
ρbaL(a 2 + L2 ) = M (a 2 + L2 )
12
12
- 64 -
Secções circulares:
Se a secção transversal é, por exemplo, um círculo de raio R
então é conveniente utilizar coordenadas polares:
- 65 -
Admita-se agora que a secção transversal é muito pequena, a
situação típica para barras muito finas)
Nessas condições, basta considerar na expressão anterior que
a ≈ 0,
obtendo-se:
I yy = M
1 2
L
12
Caso não tivéssemos obtido a expressão genérica para barras
prismáticas poderíamos efectuar o integral tendo já em conta a
M
dM
=
dx :
esbelteza da barra, quer dizer, admitir
L
M 2
1 2
I yy = ∫
x dx = M
L
−L / 2 L
12
L/2
- 66 -
Veja-se agora o caso do momento de inércia calculado não para o
centro da barra mas para um eixo paralelo a y centrado numa das
extremidades da barra:
I y'y' = ∫
L
0
M 2
1
x dx = ML2
L
3
Vê-se assim que o momento de inércia aumenta de uma
quantidade
∆:
I y ' y ' = I yy + ∆
1
1
1
L
∆ = ML2 − ML2 = ML2 = M  
3
12
4
2
2
Para este caso é fácil de ver que o aumento do momento de
inércia é o produto da massa total pelo quadrado da distância
entre os eixos
y
e
y' .
Em geral não é tão fácil de ver mas este resultado é aplicável a
todos os casos, ou seja, o momento de inércia de um corpo rígido
em relação a um eixo com uma determinada direcção é mínimo
quando o eixo passa no centro de massa e aumenta à medida que
o eixo se afasta do centro de massa
- 67 -
Tensor de inércia referido a eixos paralelos
Conhecidas as componentes do tensor de inércia do corpo rígido
no respectivo centro de massa G pode, com uma operação
simples, obter-se as componentes do mesmo tensor agora
referido a um referencial de eixos paralelos aos iniciais noutro
ponto qualquer.
Essa operação não é mais que a aplicação do Teorema de
Lagrange-Steiner ou teorema dos eixos paralelos.
Sejam dois sistemas de eixos paralelos um dos quais está
centrado no centro de massa G e o outro é um ponto genérico O.
Conhecidas as componentes do tensor de inércia em G podem
obter-se as correspondentes componentes em O sobrepondo aos
valores em G o produto da massa total do corpo:
• pelo quadrado da distância entre os eixos paralelos, no caso
dos momentos de inércia:
- 68 -
• pelo produto das distâncias entre os eixos paralelos envolvidos,
no caso dos produtos de inércia:
Na sua forma mais sintética:
Este teorema pode ser usado também para encontrar o tensor de
inércia num ponto genérico P conhecido o tensor no ponto O que
não o centro de massa. Basta aplicar o teorema dos eixos
paralelos duas vezes.
O Teorema de Lagrange-Steiner simplifica significativamente o
cálculo de momentos de inércia mesmo quando se recorre à
integração directa.
- 69 -
- 70 -