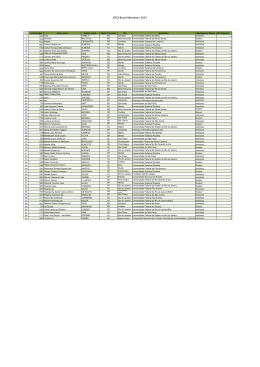
1
Distribuição Amostral dos Estimadores
1. ESTIMAÇÃO E INTERVALO DE CONFIANÇA
Estimação é o processo que consiste no uso de dados da amostra (dados amostrais) para
estimar valores de parâmetros populacionais desconhecidos, tais como média, desvio padrão,
proporção, etc.
Estudaremos como se distribuem por amostragem dois estimadores: o estimador x da
média µ e o estimador p da proporção populacional p.
2. DISTRIBUIÇÃO AMOSTRAL DA MÉDIA
De uma população X, tiramos uma amostra de tamanho n constituída pelos elementos x1, x2,
x3, . . . , xn.
O estimador da média µ populacional na amostra é: x =
1 n
. ∑ xi
n i =1
Para exemplificar, vamos considerar uma população finita X: 1, 2, 3, 4, 5, temos n = 5
elementos.
n
E ( x ) = µ x = . ∑ x i . p ( xi )
∴
i =1
E (x ) = µ x =
∴ µ x = .E ( x ) = 3
Amostra → x → (um valor)
População → µ = x → (mesmo valor).
1
15
. (1 + 2 + 3 + 4 + 5) =
= 3
5
5
2
3. ESTIMATIVA DE MÉDIAS DE UMA POPULAÇÃO
Para efetuar a Estimativa de Médias de uma População utiliza-se desvio padrão da
distribuição que constitui a amostra (distribuição amostral), deve-se levar em consideração se o
desvio padrão da população é ou não conhecido.
Estimativa intervalar da média:
Amostra → x
População → µ ± zS
onde: S =
σx
n
Sabendo que:
x
=
Média da amostra.
µ
=
Média da população.
S
=
Desvio padrão da amostra.
σx
=
Desvio padrão da população.
n
=
Número de elementos da amostra.
z
=
Número de desvios padrão da tabela normal.
Assim teremos a estimativa intervalar: µ ± z .
σx
n
Obs.: Para amostras de 30 ou menos elementos, é importante saber que a população
submetida à amostragem tem distribuição normal ou aproximadamente normal.
Exemplo: Extraímos uma amostra de 100 elementos extraída de uma população aproximadamente
normal, cujo desvio padrão é igual a 2, forneceu uma média x = 35,6 , construir intervalos de
confiança de 90%, 95% e 99% para a média dessa população.
Primeiro vamos calcular z:
Quando observamos a representação da distribuição normal reduzida, sabemos que toda a área
compreendida entre a curva e sua base tem valor 1, logo a parte hachurada tem valor 0,5.
3
No semestre anterior calculávamos z e então encontrávamos a área correspondente e, sim, a
probabilidade desejada. Agora a ação será inversa. Desejamos, em nosso exemplo acima, para seu
primeiro intervalo 90% de confiança, então fazemos: 90% * 0,5 = 0,45 .
Conhecendo a área que nos dá 90% de confiança no resultado, vamos até a tabela para a
Distribuição Normal Padronizada e encontramos o valor mais próximo de 0,45, que é 0,4494974.
Para este valor temos (considerando a linha e a coluna) z = 1,64 (observe a tabela na página 4 com
os devidos destaques).
O mesmo faremos para 95% e 99%, veja:
95% * 0,5 = 0,475 na tabela z = 1,96.
99% * 0,5 = 0,495 na tabela z = 2,58.
Confiança
Desejada
“z”
Fórmula
90 %
1,64
µ ± 1,64 .
95 %
1,96
µ ± 1,96 .
99 %
2,58
µ ± 2,58 .
Intervalo de Confiança
σx
n
σx
n
σx
n
Podemos representar da seguinte forma:
P ( 35,272 ≤ µ ≤ 35,928 ) = 0,90
P ( 35,208 ≤ µ ≤ 35,992 ) = 0,95
P ( 35,084 ≤ µ ≤ 35,116 ) = 0,99
35,6 ± 1,64 .
35,6 ± 1,96 .
35,6 ± 2,58 .
2
100
2
100
2
100
= 35,6 ± 0,328
= 35,6 ± 0,392
= 35,6 ± 0,516
4
5
4. ERRO ADMITIDO NUM INTERVALO (ERRO DE ESTIMAÇÃO)
É a diferença entre a média da amostra e a verdadeira média da população.
Como o intervalo de confiança tem centro na média da amostra, o erro máximo provável que
está sendo admitido é igual à metade da amplitude do intervalo.
O erro de estimação pode ser descrito pela relação: E = z .
E
=
Erro de Estimação.
σx
=
Desvio padrão da população.
n
=
Número de elementos da amostra.
z
=
Número de desvios padrão da tabela normal.
σx
n
, onde:
Percebemos que quando aumentamos z ou σ x este erro potencial aumenta. Podemos
concluir também que maiores amostras (aumenta n) possuem um potencial de erro menor.
No caso do desvio padrão populacional desconhecido que é habitualmente a situação mais
comum, teremos o mesmo raciocínio.
Entretanto, em nossa avaliação devemos verificar o tamanho da amostra (n), se:
Quando usamos a distribuição normal
Quando usamos a distribuição t de Student
Assim nos intervalos teremos: x ± z .
S
n
ou
x ± t.
S
n
.
5. DISTRIBUIÇÃO t DE STUDENT
Para pequenas amostras a distribuição normal apresenta valores menos precisos, o que nos
leva a utilizar um modelo melhor. Por isso iremos conhecer a distribuição t de Student.
A principal diferença entre a distribuição normal e a t de Student é que esta tem mais área
nas caudas.
6
Existe um valor de t para cada tamanho de amostra, sendo que à medida que a amostra (n)
cresce, a distribuição t de Student se aproxima da distribuição normal.
Para calcular o valor de t a ser usado é necessário ter:
Um nível de confiança desejado.
Qual o número de graus de liberdade a ser utilizado:
Por exemplo:
Sabendo-se que uma amostra tem 25 elementos, que a sua média 150 e desvio padrão igual a
10. Represente um intervalo de confiança em nível de 90%.
Como a amostra é menor de 30 elementos, então iremos usar a distribuição t de Student. Se
desejarmos um intervalo de confiança de 90%, temos:
α
2
5%
(1 − α )
90 %
α
2
5%
7
Para trabalharmos com a tabela, encontramos o número de graus de liberdade que é: (n − 1) ,
logo (25 − 1) = 24 .
O nível de confiança desejado é ( 1 − α
)
= 1 − 0,9 = 0,1
Conhecendo o número de graus de liberdade e o nível de confiança desejado, vamos a tabela
e encontramos o valor t, neste caso igual a 1,7109 (veja tabela abaixo).
8
Assim: x ± t .
S
⇒ 150 ± 1,7109 .
n
10
25
⇒ 150 ± 3,4218
P ( 146,5782 ≤ x ≤ 153,4218 ) = 0,90
6. DETERMINAÇÃO DO TAMANHO DA AMOSTRA
O tamanho da amostra depende de 3 fatores, conforme abaixo:
√ O grau de confiança desejado (z);
√ Quantidade de dispersão entre os valores individuais da população ( σ x );
√ Erro tolerável ou admitido (E).
 σ 
Sendo a fórmula para encontrarmos o tamanho da amostra: n =  z . x  .
 E 
2
Por exemplo:
Qual o tamanho de amostra necessária para se estimar a média de uma população infinita
cujo desvio padrão é igual a 4, com 98% de confiança e erro de 0,5?
 σ 
n =  z. x 
 E 
2
98 % * 0,5 = 0,49 o mais próximo possível, ver a tabela na página 9, onde z = 2,33.
4 

n =  2,33.

0,5 

n = ( 18,64 )
2
2
∴
n ≈ 347,4496
Lembramos que z foi retirado da tabela normal. Logo, precisamos de uma amostra com 348
elementos.
9
10
Distribuição de t (Student)
gl\P
01
02
03
04
05
0,90
0,158
0,142
0,137
0,134
0,132
0,80
0,325
0,289
0,277
0,271
0,267
0,70
0,510
0,445
0,424
0,414
0,408
0,60
0,727
0,617
0,584
0,569
0,559
0,50
1,000
0,816
0,765
0,741
0,727
0,40
1,376
1,061
0,978
0,941
0,920
0,30
1,963
1,386
1,250
1,190
1,156
0,20
3,078
1,886
1,638
1,533
1,476
0,10
6,314
2,920
2,353
2,132
2,015
0,05
12,706
4,303
3,182
2,776
2,571
0,02
31,821
6,965
4,541
3,747
3,365
0,01
63,657
9,925
5,541
4,604
4,032
0,001
636,619
31,598
12,924
8,610
6,869
06
07
08
09
10
0,131
0,130
0,130
0,129
0,129
0,265
0,263
0,262
0,261
0,260
0,404
0,402
0,399
0,398
0,397
0,553
0,549
0,546
0,543
0,542
0,718
0,711
0,706
0,703
0,700
0,906
0,896
0,889
0,883
0,879
1,134
1,119
1,108
1,100
1,093
1,440
1,415
1,397
1,383
1,372
1,943
1,895
1,860
1,833
1,812
2,447
2,365
2,306
2,262
2,228
3,143
2,365
2,896
2,821
2,764
3,707
3,499
3,355
3,250
3,169
5,959
5,408
5,041
4,781
4,587
11
12
13
14
15
0,129
0,128
0,128
0,128
0,128
0,260
0,259
0,259
0,258
0,258
0,396
0,395
0,394
0,393
0,393
0,540
0,539
0,538
0,537
0,536
0,697
0,695
0,694
0,692
0,691
0,876
0,873
0,870
0,868
0,866
1,088
1,083
1,079
1,076
1,074
1,363
1,356
1,350
1,345
1,341
1,796
1,782
1,771
1,761
1,753
2,201
2,179
2,160
2,145
2,131
2,718
2,681
2,650
2,624
2,602
3,106
3,055
3,012
2,977
2,947
4,437
4,318
4,221
4,140
4,073
16
17
18
19
20
21
22
23
24
25
0,128
0,128
0,127
0,127
0,127
0,127
0,127
0,127
0,127
0,127
0,258
0,257
0,257
0,257
0,257
0,257
0,256
0,256
0,256
0,256
0,392
0,392
0,392
0,391
0,391
0,391
0,390
0,390
0,390
0,390
0,535
0,534
0,534
0,533
0,533
0,532
0,532
0,532
0,531
0,531
0,690
0,689
0,688
0,688
0,687
0,686
0,686
0,685
0,685
0,684
0,865
0,863
0,862
0,861
0,860
0,859
0,858
0,858
0,857
0,856
1,071
1,069
1,067
1,066
1,064
1,063
1,061
1,060
1,059
1,058
1,337
1,333
1,330
1,328
1,325
1,323
1,321
1,319
1,318
1,316
1,746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,583
2,567
2,552
2,539
2,528
2,518
2,508
2,500
2,492
2,485
2,921
2,898
2,878
2,861
2,845
2,831
2,819
2,807
2,797
2,787
4,015
3,965
3,922
3,883
3,850
3,819
3,792
3,767
3,745
3,726
26
27
28
29
30
0,127
0,127
0,127
0,127
0,127
0,256
0,256
0,256
0,256
0,256
0,390
0,389
0,389
0,389
0,389
0,531
0,531
0,530
0,530
0,530
0,684
0,684
0,683
0,683
0,683
0,856
0,856
0,856
0,854
0,854
1,058
1,057
1,056
1,055
1,055
1,315
1,314
1,313
1,311
1,310
1,706
1,703
1,701
1,699
1,697
2,056
2,052
2,048
2,045
2,042
2,479
2,473
2,467
2,462
2,457
2,779
2,771
2,763
2,756
2,750
3,707
3,690
3,674
3,659
3,646
40
60
120
0,126
0,126
0,126
0,255
0,254
0,254
0,388
0,387
0,386
0,529
0,527
0,526
0,681
0,679
0,677
0,851
0,848
0,845
1,050
1,046
1,041
1,303
1,296
1,289
1,684
1,671
1,658
2,021
2,000
1,980
2,423
2,390
2,358
2,704
2,660
2,617
3,551
3,460
3,373
0,126
i=infinito
0,253
0,385
0,524
0,674
0,842
1,036
1,282
1,645
1,960
2,326
2,576
3,291
i